- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математика на шахматной доске презентация
Содержание
- 1. Математика на шахматной доске
- 2. Цель работы: установить связь между способами решения
- 3. Историческая справка Почти в каждом
- 4. Математика шахматной доски В
- 5. Математика шахматной доски Согласно легенде индийский принц
- 6. Математика шахматной доски Магический квадрат порядка n
- 7. Математика шахматной доски Магический квадрат «Меланхолия» - гравюра Альбрехта Дюрера Фрагмент гравюры Дюрера «Меланхолия»
- 8. 1. d3 d6 2. е3 е6
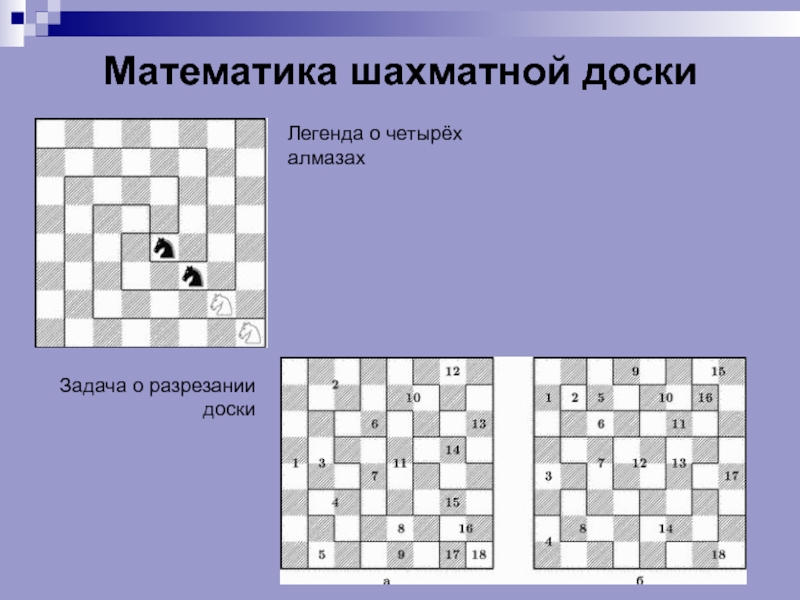
- 9. Математика шахматной доски Легенда о четырёх алмазах Задача о разрезании доски
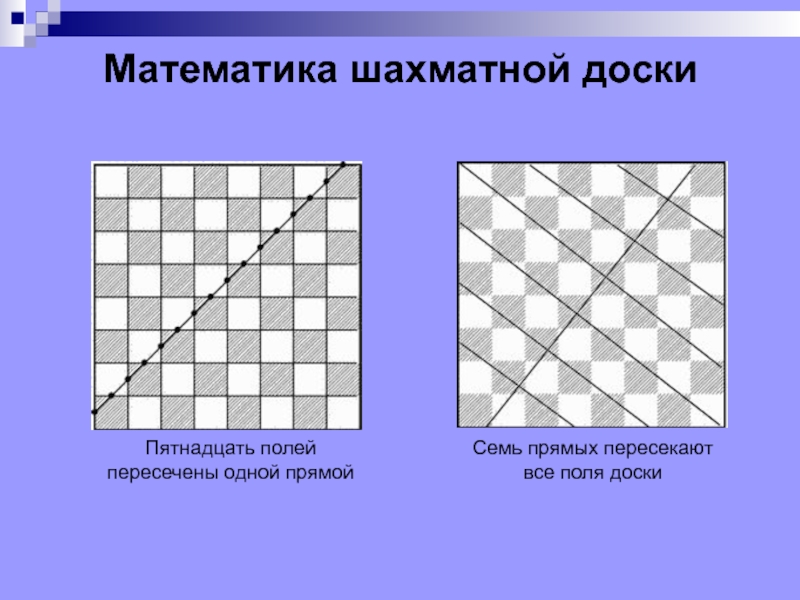
- 10. Математика шахматной доски Пятнадцать полей пересечены одной прямой Семь прямых пересекают все поля доски
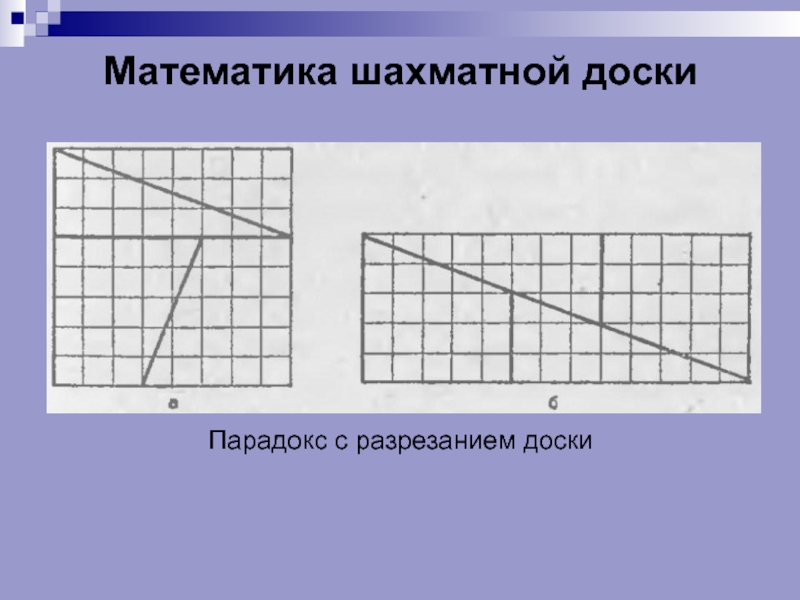
- 11. Математика шахматной доски Парадокс с разрезанием доски
- 12. Математика шахматной доски Можно ли целиком покрыть
- 13. Математика шахматной доски Домино покрывают доску Пусть
- 14. Математика шахматных фигур Задача об обходе
- 15. Математика шахматных фигур
- 16. Шахматы справедливо считают единственной игрой из всех,
- 17. Спасибо за внимание!
Слайд 2Цель работы: установить связь между способами решения математических и шахматных задач.
Задачи:
1.
2. Продемонстрировать математические решения задач, связанных с шахматной доской.
3. Продемонстрировать математические решения задач, связанных с шахматными фигурами.
Слайд 3Историческая справка
Почти в каждом сборнике олимпиадных математических задач или
Леонард Эйлер
(1707 – 1783)
Карл Фридрих Гаусс
(1777 – 1855)
Слайд 4Математика шахматной доски
В математических задачах и головоломках на
Слайд 5Математика шахматной доски
Согласно легенде индийский принц решил наградить изобретателя шахмат и
Легенда о происхождении шахмат
Начальное положение фигур в шахматах
Изобретатель потребовал 1+2+22+... +263 = 264 -1
зерен. Это число записывается двадцатью цифрами, является фантастически большим и заведомо превосходит количество пшеницы, собранной человечеством до настоящего времени. Подсчет показывает, что амбар для хранения необходимого зерна с площадью основания 80 м2 должен простираться от Земли до Солнца.
Слайд 6Математика шахматной доски
Магический квадрат порядка n представляет собой квадратную таблицу nхn,
Магический квадрат
Слайд 7Математика шахматной доски
Магический квадрат
«Меланхолия» - гравюра Альбрехта Дюрера
Фрагмент гравюры Дюрера «Меланхолия»
Слайд 81. d3 d6
2. е3 е6
3. bЗ b6
4. g3
5. с3 с6
6. f3 f6
7. c4 c5
8. f4 f5
9. Кc3 Кc6
10. Кf3 Кf6
11. Лb1 Лb8
12. Лgl Лg8
Математика шахматной доски
Альмуджаннах
Слайд 10Математика шахматной доски
Пятнадцать полей пересечены одной прямой
Семь прямых пересекают все поля
Слайд 12Математика шахматной доски
Можно ли целиком покрыть домино квадрат 8x8, из которого
Задача о домино
Слайд 13Математика шахматной доски
Домино покрывают доску
Пусть на шахматной доске вырезаны два поля
Слайд 14Математика шахматных фигур
Задача об обходе конём всех клеток шахматной доски
Решение
Первый полумагический обход конём всех клеток шахматной доски
Слайд 15
Математика шахматных фигур
Каждая не занятая ладьёй клетка находится под
Какое наименьшее количество ладей можно поставить на шахматной доске так, чтобы каждая не занятая ладьёй клетка находилась под боем хотя бы трёх из них?
Слайд 16Шахматы справедливо считают единственной игрой из всех, придуманных человеком, в которой
Занятие шахматами способствует развитию математических способностей человека. Шахматы – это и вид интеллектуальной борьбы, и соревнование, а любое соревнование совершенствует сильные черты личности.
В ходе выполнения работы выявлены следующие математические методы, используемые при решении задач на шахматную тему: метод раскраски, метод разрезания фигур.
Собственный опыт позволяет мне при игре в шахматы использовать некоторое математическое видение ситуации, которое помогает не только просчитывать будущие шахматные ходы, но и пытаться понять принцип выигрыша.
Заключение