- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Выборочное наблюдение презентация
Содержание
- 1. Выборочное наблюдение
- 2. Понятие выборочного наблюдения. Выборочное наблюдение – это
- 3. Вся исследуемая совокупность называется генеральной; Единицы подлежащие наблюдению составляют выборочную совокупность или выборку.
- 4. Условные обозначения
- 5. Цель выборочного наблюдения Определение параметров генеральной совокупности на основе показателей выборочной совокупности.
- 6. Выборочный метод обладает следующими достоинствами: относительно небольшие
- 7. Выборочные оценки отличаются от генеральных параметров
- 8. Различают два вида отбора – повторный
- 9. Возможны три способа отбора: случайный; отбор единиц
- 10. Различают следующие виды выборочного наблюдения: Типическая (расслоенная
- 11. Определение ошибки выборки средняя (стандартная), предельная относительная
- 12. При случайном и механическом отборах средняя
- 13. На практике величина дисперсии признака в
- 14. При большой численности выборочной совокупности сомножитель
- 15. Величина дисперсии доли в генеральной совокупности
- 16. При расчете средней ошибки выборочной доли
- 17. Формула для расчета средней ошибки выборочной доли для повторного отбора
- 18. Формула для расчета средней ошибки выборочной доли для бесповторного отбора
- 19. Предельная ошибка выборки
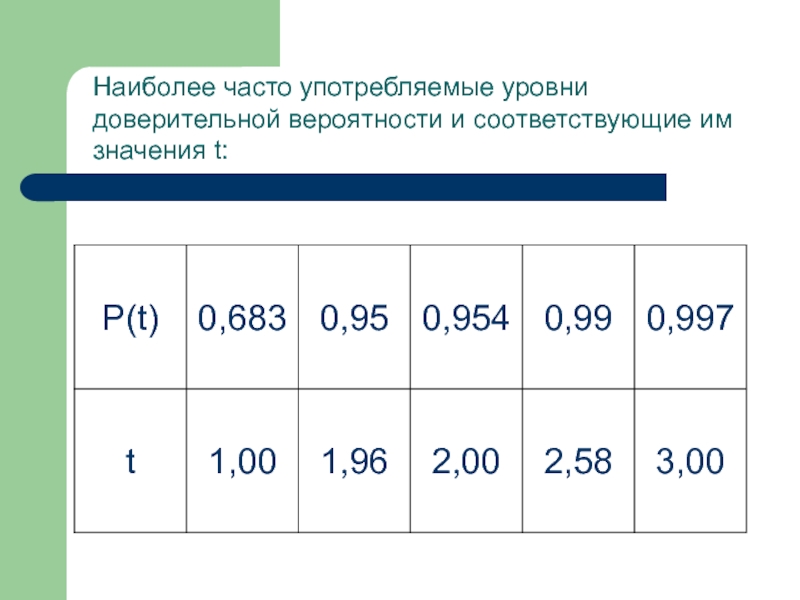
- 20. Наиболее часто употребляемые уровни доверительной вероятности и соответствующие им значения t:
- 21. Зная величину выборочной средней () или
- 22. Пример: Для определения среднего срока пользования
- 23. Нахождения необходимой численности выборки на практике
- 24. Если полученный объем выборки превышает 5% численности генеральной совокупности, расчеты корректируют «на бесповторность»:
- 25. При решении задачи определения объема выборки
- 26. Для оценки величины генеральной дисперсии можно использовать:
- 27. 3. дисперсию, определенную из соотношения для асимметричного распределения:
- 28. 4. дисперсию, вычисленную из соотношения для нормального распределения:
- 29. Пример. Определить численность выборки по следующим
- 30. Относительная ошибка выборки характеризует относительную погрешность выборочного наблюдения
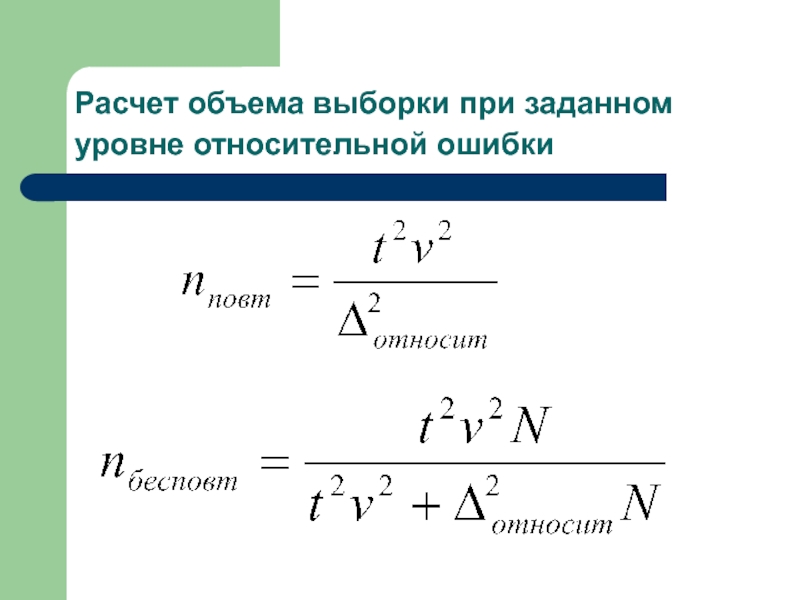
- 31. Расчет объема выборки при заданном уровне относительной ошибки
- 32. Пример. В городе зарегистрировано 30 тыс
Слайд 2Понятие выборочного наблюдения.
Выборочное наблюдение – это такой вид статистического наблюдения, при
Слайд 3
Вся исследуемая совокупность называется генеральной;
Единицы подлежащие наблюдению составляют выборочную совокупность или
Слайд 5Цель выборочного наблюдения
Определение параметров генеральной совокупности на основе показателей выборочной совокупности.
Слайд 6Выборочный метод обладает следующими достоинствами:
относительно небольшие (по сравнению со сплошным наблюдением)
оперативность получения результатов;
широкая область применения;
высокая достоверность результатов.
Слайд 7
Выборочные оценки отличаются от генеральных параметров за счет ошибки наблюдения и
Слайд 8Различают два вида отбора
– повторный
соответствует схеме «возвращенного шара».
- бесповторный.
Слайд 9Возможны три способа отбора:
случайный;
отбор единиц по определенной схеме;
сочетание первого и второго
Слайд 10Различают следующие виды выборочного наблюдения:
Типическая (расслоенная или стратифицированная)
Серийная (гнездовая)
Многоступенчатая
Многофазовая
Слайд 12При случайном и механическом отборах
средняя ошибка выборки для средней величины
При бесповторном отборе:
Слайд 13
На практике величина дисперсии признака в генеральной совокупности ,
Слайд 14
При большой численности выборочной совокупности сомножитель
стремится к
Слайд 15
Величина дисперсии доли в генеральной совокупности определяется по формуле:
где p –
Слайд 16
При расчете средней ошибки выборочной доли дисперсия доли в генеральной совокупности,
где w – доля единиц, обладающих каким-либо значением признака в выборочной совокупности.
Слайд 19Предельная ошибка выборки
где t – коэффициент доверия, который определяется по
Слайд 20Наиболее часто употребляемые уровни доверительной вероятности и соответствующие им значения t:
Слайд 21
Зная величину выборочной средней () или доли (w), а также предельную
Слайд 22
Пример:
Для определения среднего срока пользования краткосрочным кредитом в банке была произведена
Слайд 23Нахождения необходимой численности выборки
на практике расчет объема выборки производят по
Слайд 24
Если полученный объем выборки превышает 5% численности генеральной совокупности, расчеты корректируют
Слайд 25
При решении задачи определения объема выборки величина допустимой предельной ошибки и
Слайд 26Для оценки величины генеральной дисперсии можно использовать:
выборочную дисперсию по данным прошлых
дисперсию, найденную из соотношения для среднего квадратического отклонения: