- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Выборочное наблюдение презентация
Содержание
- 1. Выборочное наблюдение
- 2. Предельная ошибка выборки
- 3. Предельная ошибка выборки Наиболее часто используют следующие уровни вероятности и соответственные им значения t:
- 4. Собственно-случайная выборка
- 5. Средняя ошибка повторной собственно-случайной выборки – объем (число единиц) выборочной совокупности n
- 6. Предельная ошибка повторной собственно-случайной выборки При
- 7. Границы генеральной доли – выборочная доля w
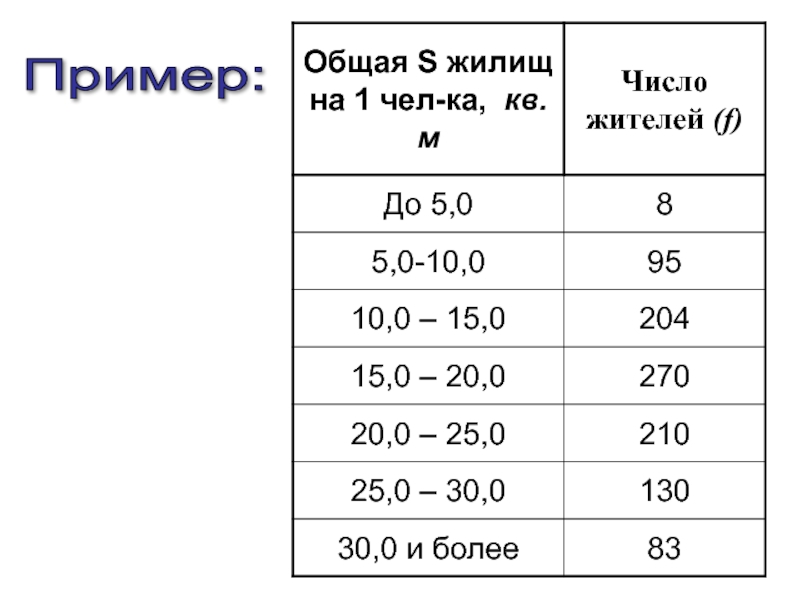
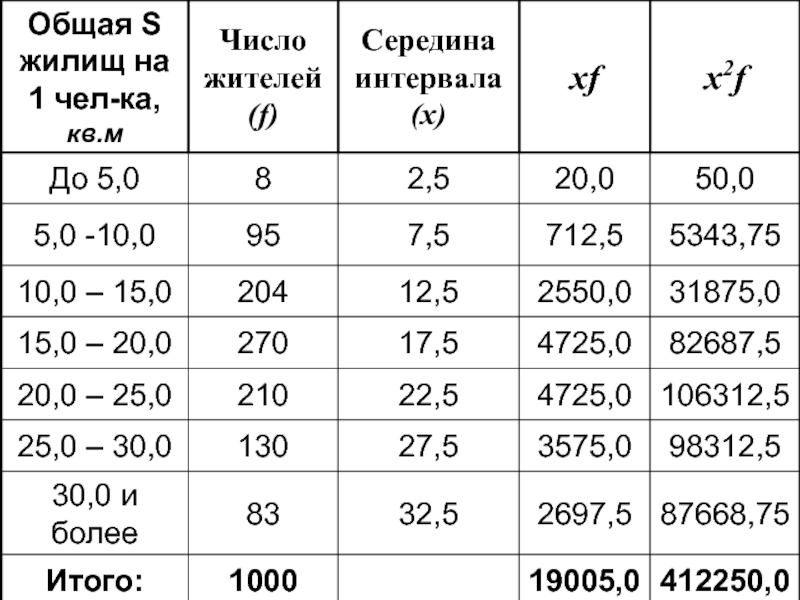
- 8. Пример:
- 10. Вероятность 0,954 (t=2)
- 11. Средняя ошибка собственно-случайной бесповторной выборки – объем (число единиц) генеральной совокупности N
- 12. Если предположить, что данные – результат 5%-ого
- 13. Обеспеченность жильем
- 14. Необходимый объем выборки
- 15. Если предположить, что нас устроят границы средней
- 16. Необходимый объем выборки (при бесповторном отборе)
- 17. Определим численность собственно-случайной бесповторной выборки с предельной
- 18. Пример: Если дисперсия альтернативного признака неизвестна, то можно использовать max возможное значение
- 19. Механическая выборка
- 20. Пример: Кол-во предприятий (N) = 6000
- 21. Типическая выборка
- 22. 1 вариант: При типической выборке, пропорциональной
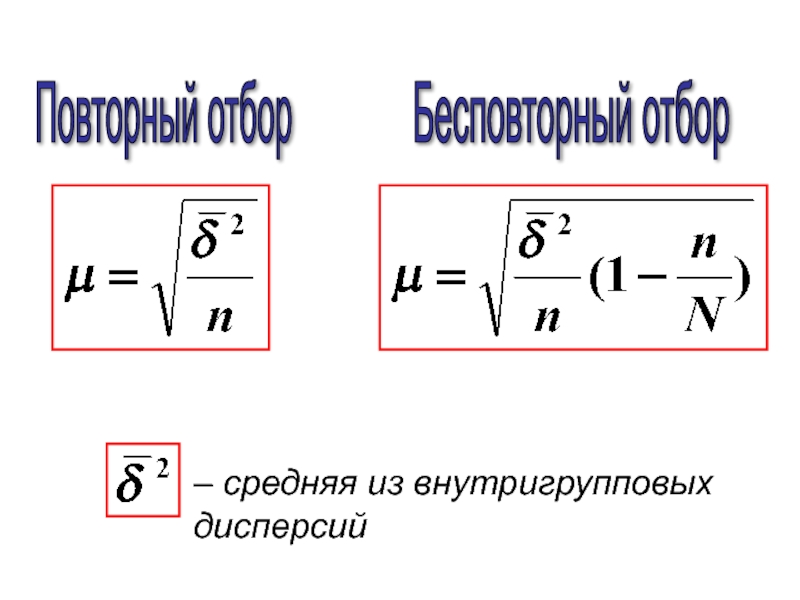
- 23. Повторный отбор – средняя из внутригрупповых дисперсий Бесповторный отбор
- 24. Пример:
- 25. Вероятность 0,954 (t=2)
- 26. Выборочная средняя: Среднее число дней временной нетрудоспособности
- 27. Необходимый объем типической выборки (при повторном отборе)
- 28. (при бесповторном отборе) Необходимый объем типической выборки
- 29. Определим среднее число дней временной нетрудоспособности одного
- 30. Распределим эту численность на 3 цеха предприятия пропорционально их размерам
- 31. 2 вариант: При отборе единиц, пропорциональным
- 32. Повторный отбор Бесповторный отбор
- 33. Определим необходимый объем выборки по каждому цеху,
- 34. Во 2 варианте средняя и предельная ошибка
- 35. Серийная выборка
- 36. Повторный отбор Бесповторный отбор –
- 37. Межгрупповая дисперсия при равновеликих группах: –
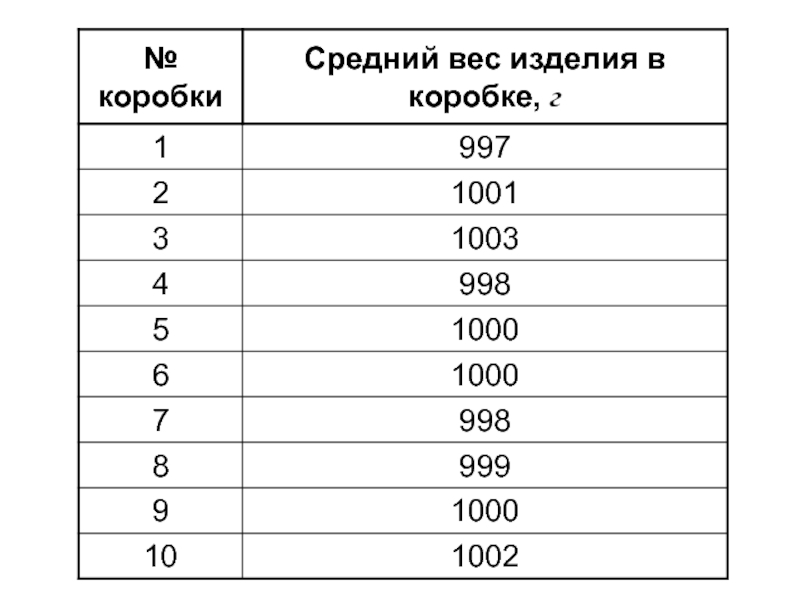
- 39. Межгрупповая дисперсия: С вероятностью 0,954 определить границы среднего веса изделия во всей партии: 1) 2)
- 40. Вероятность 0,954 (t=2) 3) Средний вес изделия
- 41. Необходимый объем серийной выборки (при повторном отборе)
- 42. (при бесповторном отборе) Необходимый объем серийной выборки
- 43. Определим границы среднего веса изделия с предельной
Предельная ошибка выборки
Слайд 3Предельная ошибка выборки
Наиболее часто используют следующие уровни вероятности и соответственные
им значения t:
Слайд 5Средняя ошибка повторной собственно-случайной выборки
– объем (число единиц) выборочной совокупности
n
Слайд 6Предельная ошибка повторной собственно-случайной выборки
При заданной вероятности генеральная средняя будет
находиться в следующих пределах:
Слайд 11Средняя ошибка собственно-случайной бесповторной выборки
– объем (число единиц) генеральной совокупности
N
Слайд 12Если предположить, что данные – результат 5%-ого бесповторного отбора (1000ед.-5%, 20000ед.-100%):
Уменьшение
предельной ошибки выборки
Сужение границ генеральной средней
Слайд 15Если предположить, что нас устроят границы средней S, приходящейся на 1
чел-ка, с точностью 0,5 кв.м
Достаточно в порядке собственно-случайной выборки обследовать 821 чел.
Слайд 17Определим численность собственно-случайной бесповторной выборки с предельной ошибкой, не превышающей 0,5
кв.м
Для достижения заданной точности необходимо обследовать не менее 788 чел.
Слайд 18Пример:
Если дисперсия альтернативного признака неизвестна, то можно использовать max возможное
значение
Слайд 20Пример:
Кол-во предприятий (N) = 6000
Ошибка определения числа занятых +/-2 чел.
Вероятность
(P) = 0,997 (t=3)
Среднее квадратичное отклонение = 9чел.
Среднее квадратичное отклонение = 9чел.
Интервал отбора:
Процент отбора:
Слайд 221 вариант:
При типической выборке, пропорциональной объему типических групп
– объем выборки из
i-ой группы
ni
– объем i-ой группы
Ni
Слайд 26Выборочная средняя:
Среднее число дней временной нетрудоспособности одного работника в целом по
предприятию находится в пределах:
Слайд 29Определим среднее число дней временной нетрудоспособности одного работника с предельной ошибкой
0,5 дня
Необходимо обследовать выборочным методом не менее 421 чел.
Слайд 312 вариант:
При отборе единиц, пропорциональным вариации признака в типических группах
Число наблюдений
по каждой группе
Слайд 33Определим необходимый объем выборки по каждому цеху, пропорциональный вариации изучаемого признака,
при условии, что в целом выборка составляет 10% или 320 чел-к
Слайд 34Во 2 варианте средняя и предельная ошибка будут несколько меньше, что
отразится и на границах
генеральной средней
генеральной средней
Слайд 37Межгрупповая дисперсия при равновеликих группах:
– общая средняя по всей выборочной
совокупности
– средняя из i-ой серии
Слайд 39Межгрупповая дисперсия:
С вероятностью 0,954 определить границы среднего веса изделия во всей
партии:
1)
2)
Слайд 40Вероятность 0,954 (t=2)
3)
Средний вес изделия в целом по всей партии продукции
находится в пределах:
Слайд 43Определим границы среднего веса изделия с предельной ошибкой +/- 0,8г
Необходимо обследовать
не менее 18 коробок с изделиями
