- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дифференциальные уравнения. Линейные уравнения с постоянными коэффициентами презентация
Содержание
- 1. Дифференциальные уравнения. Линейные уравнения с постоянными коэффициентами
- 2. Линейные уравнения с постоянными коэффициентами Однородные
- 3. Линейные уравнения с постоянными коэффициентами Определение. Алгебраическое
- 4. Линейные уравнения с постоянными коэффициентами Примеры. 1.
- 5. Линейные уравнения с постоянными коэффициентами Примеры. 2.
- 6. Линейные уравнения с постоянными коэффициентами Свойства решений
- 7. Линейные уравнения с постоянными коэффициентами Свойства решений
- 8. Линейные уравнения с постоянными коэффициентами 2. Критерий
- 9. Линейные уравнения с постоянными коэффициентами Определение ФСР.
- 10. Линейные уравнения с постоянными коэффициентами Определение ФСР.
- 11. Линейные уравнения с постоянными коэффициентами Теорема
- 12. Линейные уравнения с постоянными коэффициентами ФСР в
- 13. Линейные уравнения с постоянными коэффициентами Случай кратных
- 14. Линейные уравнения с постоянными коэффициентами Случай кратных
- 15. Линейные уравнения с постоянными коэффициентами ФСР в
- 16. Линейные уравнения с постоянными коэффициентами Преобразуем функции
- 17. Линейные уравнения с постоянными коэффициентами Примеры. 1.
- 18. Линейные уравнения с постоянными коэффициентами Примеры. 2.
- 19. Линейные уравнения с постоянными коэффициентами 2. Случай
- 20. Линейные уравнения с постоянными коэффициентами Неоднородные уравнения
- 21. Линейные уравнения с постоянными коэффициентами Неоднородные уравнения
- 22. Линейные уравнения с постоянными коэффициентами 2. Принцип суперпозиции.
- 23. Линейные уравнения с постоянными коэффициентами 2. Принцип суперпозиции. Доказательство.
- 24. Линейные уравнения с постоянными коэффициентами Теорема о
- 25. Линейные уравнения с постоянными коэффициентами Неоднородные уравнения
- 26. Линейные уравнения с постоянными коэффициентами Примеры. 1.
- 27. Линейные уравнения с постоянными коэффициентами 2.
- 28. Линейные уравнения с постоянными коэффициентами Пример 3.
- 29. Линейные уравнения с постоянными коэффициентами Пример 4.
- 30. Линейные уравнения с постоянными коэффициентами Линейные неоднородные
- 31. Линейные уравнения с постоянными коэффициентами Частный случай.
- 32. Линейные уравнения с постоянными коэффициентами Пример.
- 33. Линейные уравнения с постоянными коэффициентами Уравнение колебаний.
- 34. Линейные уравнения с постоянными коэффициентами Характеристическое уравнение:
- 35. Линейные уравнения с постоянными коэффициентами Вынужденные колебания.
Линейные уравнения с постоянными коэффициентами
Однородные Д.У. с постоянными коэффициентами. Рассмотрим уравнение где
Слайд 2Линейные уравнения с постоянными коэффициентами
Однородные Д.У. с постоянными коэффициентами.
Рассмотрим уравнение
где
- постоянные действительные числа
Пусть функция - решение Д.У.
Пусть функция - решение Д.У.
- корень алгебраического уравнения
Слайд 3Линейные уравнения с постоянными коэффициентами
Определение.
Алгебраическое уравнение
соответствующее данному ЛОДУ,
называется характеристическим уравнением.
Обратное утверждение:
Пусть
- корень характеристического уравнения.
Тогда функция -частное решение ЛОДУ.
Замечание. Алгебраическое уравнение степени n с действительными коэффициентами имеет n решений.
Тогда функция -частное решение ЛОДУ.
Замечание. Алгебраическое уравнение степени n с действительными коэффициентами имеет n решений.
Слайд 4Линейные уравнения с постоянными коэффициентами
Примеры.
1.
Замена:
Характеристическое уравнение:
- частные решения ЛОДУ.
Слайд 5Линейные уравнения с постоянными коэффициентами
Примеры.
2.
Замена:
Характеристическое уравнение:
- частные решения ЛОДУ.
Слайд 6Линейные уравнения с постоянными коэффициентами
Свойства решений ЛОДУ.
1. Линейность.
- решения ЛОДУ
- решение ЛОДУ.
Доказать самостоятельно.
- решение ЛОДУ.
Доказать самостоятельно.
Слайд 7Линейные уравнения с постоянными коэффициентами
Свойства решений ЛОДУ.
1. Линейность.
- решения ЛОДУ
- решение ЛОДУ.
Доказать самостоятельно.
Примеры.
1. - решение ЛОДУ
при любых постоянных С1 и С2.
2. - решение ЛОДУ
при любых постоянных С1 и С2.
- решение ЛОДУ.
Доказать самостоятельно.
Примеры.
1. - решение ЛОДУ
при любых постоянных С1 и С2.
2. - решение ЛОДУ
при любых постоянных С1 и С2.
Слайд 8Линейные уравнения с постоянными коэффициентами
2. Критерий линейной независимости системы решений ЛОДУ.
Пусть
-
частные решения ЛОДУ порядка n в .
Теорема.
Система функций
линейно независимая в
Теорема.
Система функций
линейно независимая в
Слайд 9Линейные уравнения с постоянными коэффициентами
Определение ФСР.
Фундаментальной системой решений (ФСР)
ЛОДУ
- порядка n
называется система
n линейно независимых решений ЛОДУ.
называется система
n линейно независимых решений ЛОДУ.
Слайд 10Линейные уравнения с постоянными коэффициентами
Определение ФСР.
Фундаментальной системой решений (ФСР)
ЛОДУ
- порядка n
называется система
n линейно независимых решений ЛОДУ.
Примеры.
1. - ФСР ЛОДУ
2. - ФСР ЛОДУ
называется система
n линейно независимых решений ЛОДУ.
Примеры.
1. - ФСР ЛОДУ
2. - ФСР ЛОДУ
Слайд 11Линейные уравнения с постоянными коэффициентами
Теорема о структуре общего решения ЛОДУ.
Пусть при
система
образует ФСР ЛОДУ порядка n.
Тогда общее решение ЛОДУ порядка n
имеет вид
с произвольными постоянными
Примеры.
1. , - общее решение ЛОДУ
2. , - общее решение ЛОДУ
образует ФСР ЛОДУ порядка n.
Тогда общее решение ЛОДУ порядка n
имеет вид
с произвольными постоянными
Примеры.
1. , - общее решение ЛОДУ
2. , - общее решение ЛОДУ
Слайд 12Линейные уравнения с постоянными коэффициентами
ФСР в случае различных действительных корней.
Доказательство (при
n=2).
1.
2.
1.
2.
образуют ФСР
Слайд 13Линейные уравнения с постоянными коэффициентами
Случай кратных действительных корней.
Пусть действительное число
- корень уравнения
кратности
В ФСР ЛОДУ ему соответствуют решений вида
кратности
В ФСР ЛОДУ ему соответствуют решений вида
Слайд 14Линейные уравнения с постоянными коэффициентами
Случай кратных действительных корней.
Пусть действительное число
- корень уравнения
кратности
В ФСР ЛОДУ ему соответствуют решений вида
Пример.
1.
2. Замена:
3. Характеристическое уравнение:
4. ФСР:
кратности
В ФСР ЛОДУ ему соответствуют решений вида
Пример.
1.
2. Замена:
3. Характеристическое уравнение:
4. ФСР:
(кратность 2)
Слайд 15Линейные уравнения с постоянными коэффициентами
ФСР в случае, когда некоторые корни комплексные.
1.
Случай простого комплексного корня.
Пусть - комплексный корень характеристического уравнения
тогда - также корень этого уравнения.
Функции
- решения ЛОДУ.
Функции линейно независимые, так как
Функции вместе с другими (n-2) -линейно независимыми решениями ЛОДУ образуют ФСР.
Пусть - комплексный корень характеристического уравнения
тогда - также корень этого уравнения.
Функции
- решения ЛОДУ.
Функции линейно независимые, так как
Функции вместе с другими (n-2) -линейно независимыми решениями ЛОДУ образуют ФСР.
Слайд 16Линейные уравнения с постоянными коэффициентами
Преобразуем функции
с помощью формулы Эйлера:
Функции
являются действительными функциями
переменной х;
являются решениями ЛОДУ;
являются линейно независимыми
являются решениями ЛОДУ;
являются линейно независимыми
Образуют
(вместе с другими)
ФСР
Слайд 17Линейные уравнения с постоянными коэффициентами
Примеры.
1. Найти ФСР уравнения
Шаг 1. Запишем
характеристическое уравнение и решим его:
Шаг 2. Запишем ФСР ЛОДУ:
Шаг 2. Запишем ФСР ЛОДУ:
Слайд 18Линейные уравнения с постоянными коэффициентами
Примеры.
2. Найти ФСР уравнения
Шаг 1. Запишем
характеристическое уравнение и решим его:
Шаг 2. Запишем ФСР ЛОДУ:
Шаг 2. Запишем ФСР ЛОДУ:
Слайд 19Линейные уравнения с постоянными коэффициентами
2. Случай кратных комплексных корней.
Пусть комплексное число
корень
кратности
число - тоже корень кратности
В ФСР ЛОДУ им соответствуют решений вида
число - тоже корень кратности
В ФСР ЛОДУ им соответствуют решений вида
Слайд 20Линейные уравнения с постоянными коэффициентами
Неоднородные уравнения с постоянными коэффициентами.
Свойства решений ЛНДУ.
.
1. - частные решения ЛНДУ
- решение ЛОДУ ,
соответствующего данному ЛНДУ.
1. - частные решения ЛНДУ
- решение ЛОДУ ,
соответствующего данному ЛНДУ.
Слайд 21Линейные уравнения с постоянными коэффициентами
Неоднородные уравнения с постоянными коэффициентами.
Свойства решений ЛНДУ.
.
1. - частные решения ЛНДУ
- решение ЛОДУ ,
соответствующего данному ЛНДУ.
Доказательство.
1. - частные решения ЛНДУ
- решение ЛОДУ ,
соответствующего данному ЛНДУ.
Доказательство.
Слайд 24Линейные уравнения с постоянными коэффициентами
Теорема о структуре общего решения ЛНДУ.
1.
- частное решение ЛНДУ порядка n.
2. - ФСР ЛОДУ ,
соответствующего данному ЛНДУ.
2. - ФСР ЛОДУ ,
соответствующего данному ЛНДУ.
Общее решение ЛНДУ имеет вид
- произвольные постоянные
Слайд 25Линейные уравнения с постоянными коэффициентами
Неоднородные уравнения с постоянными коэффициентами.
Метод неопределенных коэффициентов.
Рассмотрим
уравнение
где - постоянные коэффициенты и
имеет специальный вид.
Правило.
где - постоянные коэффициенты и
имеет специальный вид.
Правило.
Слайд 26Линейные уравнения с постоянными коэффициентами
Примеры.
1. Найти общее решение уравнения
Шаг 1.
Решим ЛОДУ, соответствующее данному ЛНДУ:
Шаг 2. Найдем частное решение ЛНДУ:
Шаг 3. Запишем общее решение ЛНДУ:
Шаг 2. Найдем частное решение ЛНДУ:
Шаг 3. Запишем общее решение ЛНДУ:
Слайд 27 Линейные уравнения с постоянными коэффициентами
2. Найти общее решение ЛНДУ
Шаг 1.
Решим ЛОДУ, соответствующее данному ЛНДУ:
Шаг 2. Найдем частное решение ЛНДУ:
Шаг 3. Запишем общее решение ЛНДУ:
Шаг 2. Найдем частное решение ЛНДУ:
Шаг 3. Запишем общее решение ЛНДУ:
Слайд 28Линейные уравнения с постоянными коэффициентами
Пример 3. Найти общее решение ЛНДУ
Шаг 1.
Решим ЛОДУ, соответствующее данному ЛНДУ:
Шаг 2. Найдем частное решение ЛНДУ:
Шаг 3. Запишем общее решение ЛНДУ:
Шаг 2. Найдем частное решение ЛНДУ:
Шаг 3. Запишем общее решение ЛНДУ:
Слайд 29Линейные уравнения с постоянными коэффициентами
Пример 4. Найти общее решение ЛНДУ
Шаг 1.
Решим ЛОДУ, соответствующее данному ЛНДУ:
Шаг 2. Найдем частное решение ЛНДУ:
Шаг 3. Запишем общее решение::
Шаг 2. Найдем частное решение ЛНДУ:
Шаг 3. Запишем общее решение::
резонанс
Слайд 30Линейные уравнения с постоянными коэффициентами
Линейные неоднородные Д.У.
Метод вариации произвольных постоянных (метод
Лагранжа).
Теорема.
- ЛНДУ порядка n с непрерывными коэффициентами.
- ФСР ЛОДУ, соответствующего данному ЛНДУ
Теорема.
- ЛНДУ порядка n с непрерывными коэффициентами.
- ФСР ЛОДУ, соответствующего данному ЛНДУ
Слайд 31Линейные уравнения с постоянными коэффициентами
Частный случай.
Рассмотрим ЛНДУ второго порядка
Пусть
- ФСР соответствующего ЛОДУ .
Тогда
Тогда
Слайд 32Линейные уравнения с постоянными коэффициентами
Пример.
Решение.
1. ЛОДУ
ФСР
2. Общее решение ЛОДУ
3. Частное решение ЛНДУ
4. Найдем
5. Общее решение ЛНДУ
2. Общее решение ЛОДУ
3. Частное решение ЛНДУ
4. Найдем
5. Общее решение ЛНДУ
Слайд 33Линейные уравнения с постоянными коэффициентами
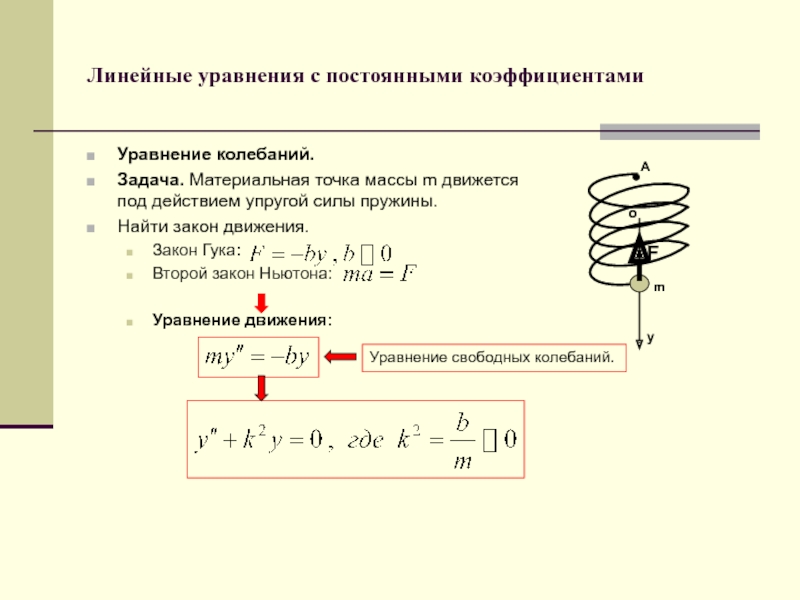
Уравнение колебаний.
Задача. Материальная точка массы m движется
под действием упругой силы пружины.
Найти закон движения.
Закон Гука:
Второй закон Ньютона:
Уравнение движения:
Найти закон движения.
Закон Гука:
Второй закон Ньютона:
Уравнение движения:
y
F
m
o
A
Уравнение свободных колебаний.
Слайд 34Линейные уравнения с постоянными коэффициентами
Характеристическое уравнение:
ФСР:
Общее решение:
Задача Коши.
Свободные колебания с амплитудой
и начальной фазой
- частота собственных колебаний
Слайд 35Линейные уравнения с постоянными коэффициентами
Вынужденные колебания. Резонанс.
- внешняя сила
- амплитуда, - частота внешней силы.
Уравнение вынужденных колебаний.
- амплитуда, - частота внешней силы.
Уравнение вынужденных колебаний.
- отсутствие резонанса
- резонанс
