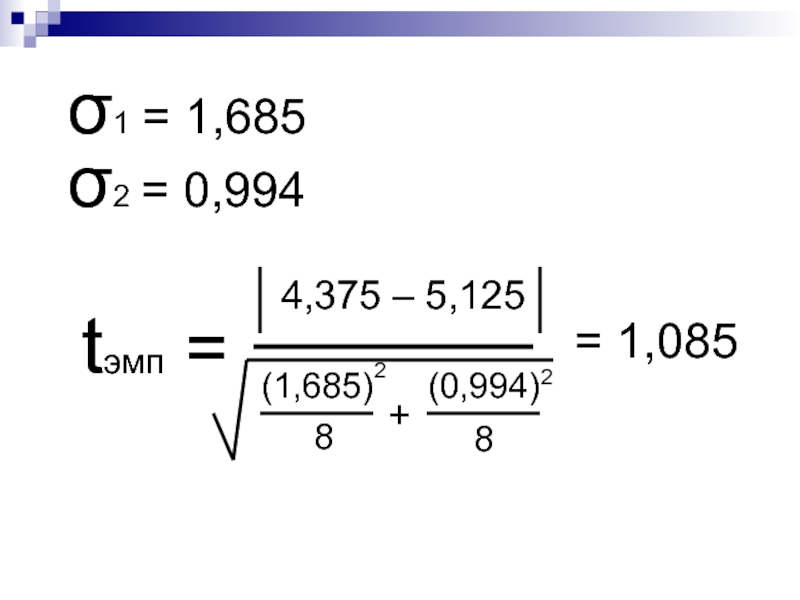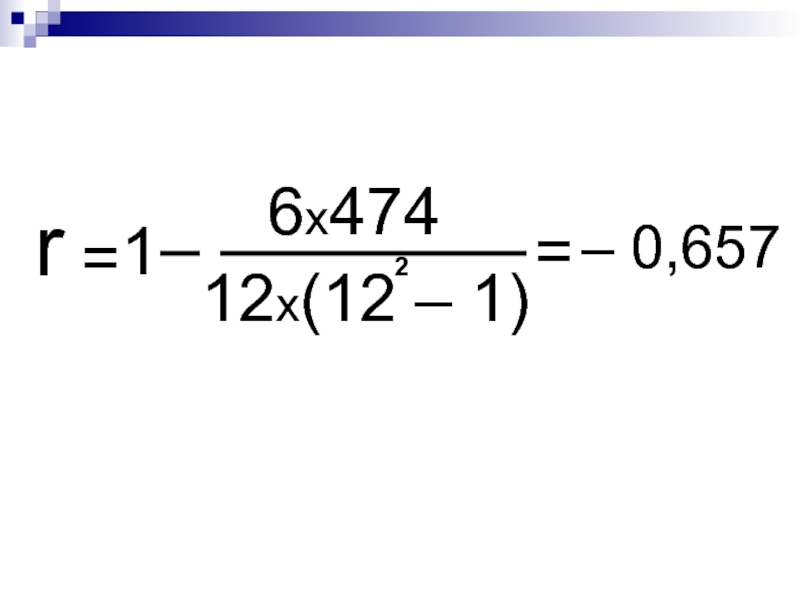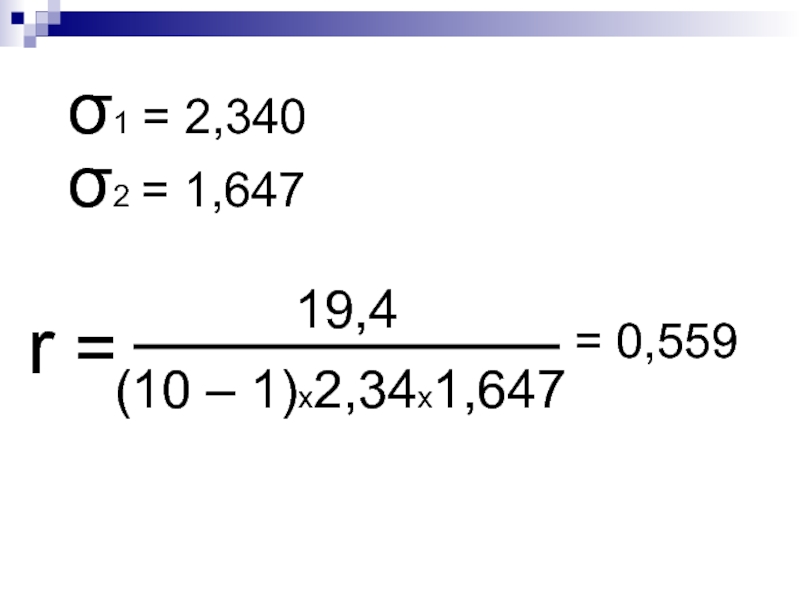- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Выборка. Генеральная выборка. Выборочные совокупности презентация
Содержание
- 1. Выборка. Генеральная выборка. Выборочные совокупности
- 2. ИЗМЕРЕНИЕ И ШКАЛЫ ШКАЛА НАИМЕНОВАНИЙ
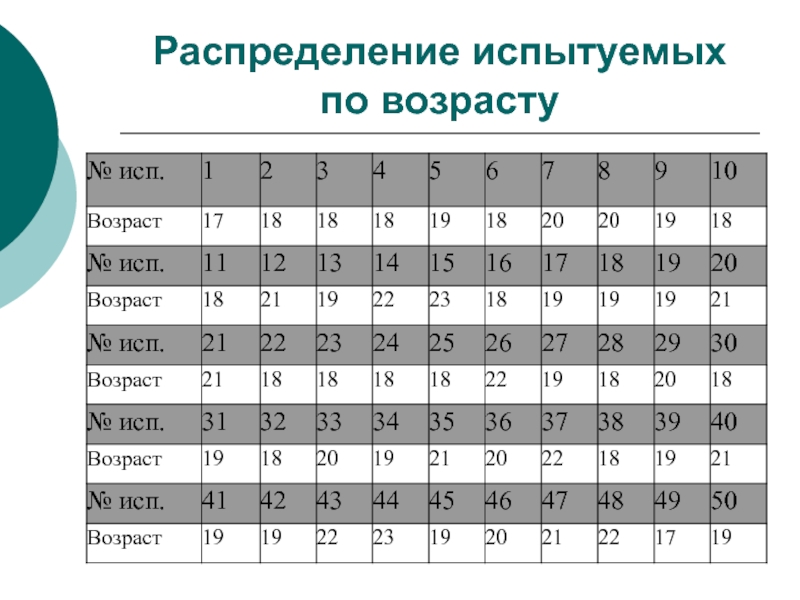
- 3. Распределение испытуемых по возрасту
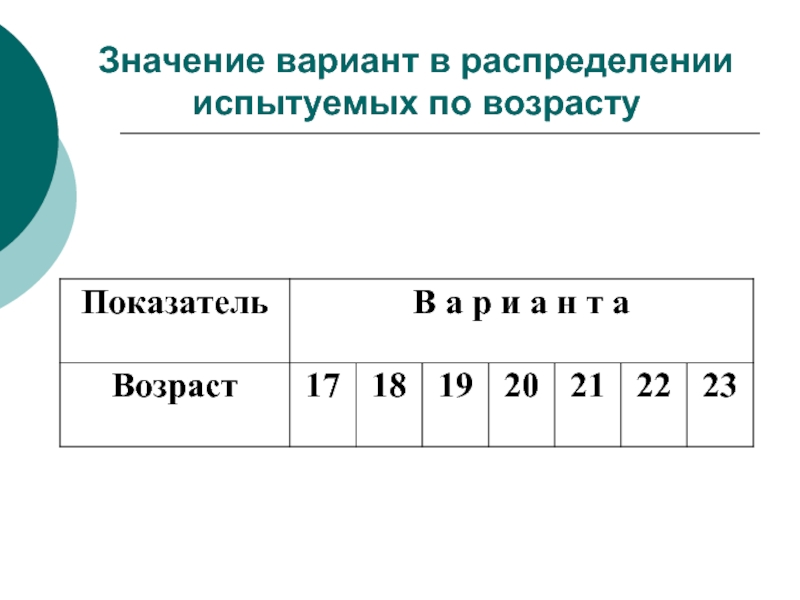
- 4. Значение вариант в распределении испытуемых по возрасту
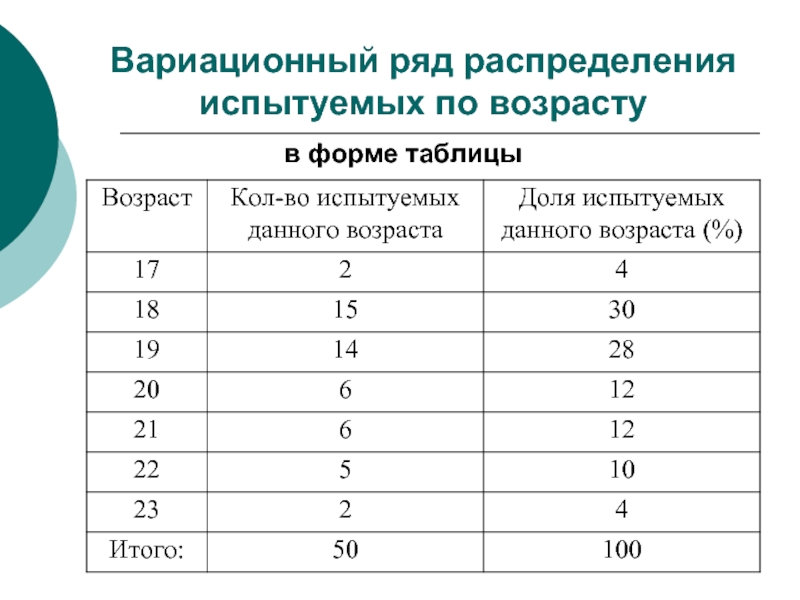
- 5. Вариационный ряд распределения испытуемых по возрасту в форме таблицы
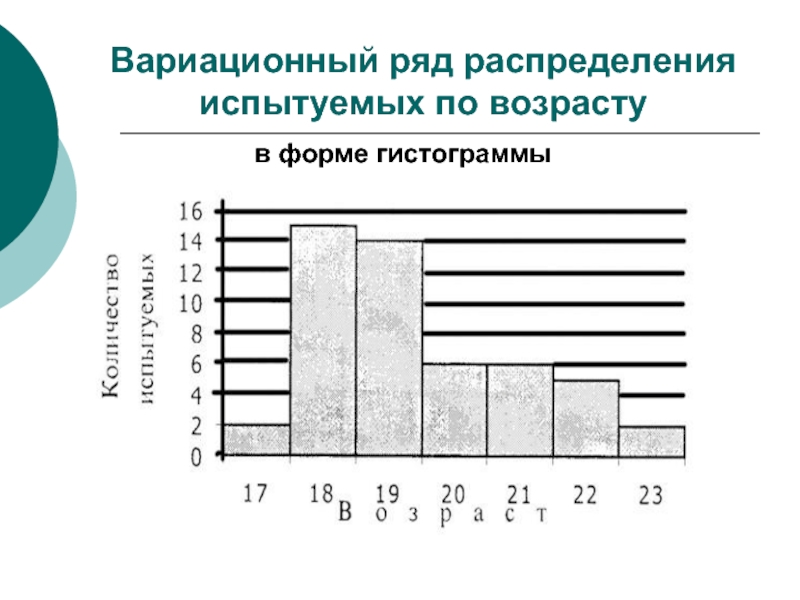
- 6. Вариационный ряд распределения испытуемых по возрасту в форме гистограммы
- 7. Вариационный ряд распределения испытуемых по возрасту
- 8. Вариационный ряд распределения испытуемых по возрасту
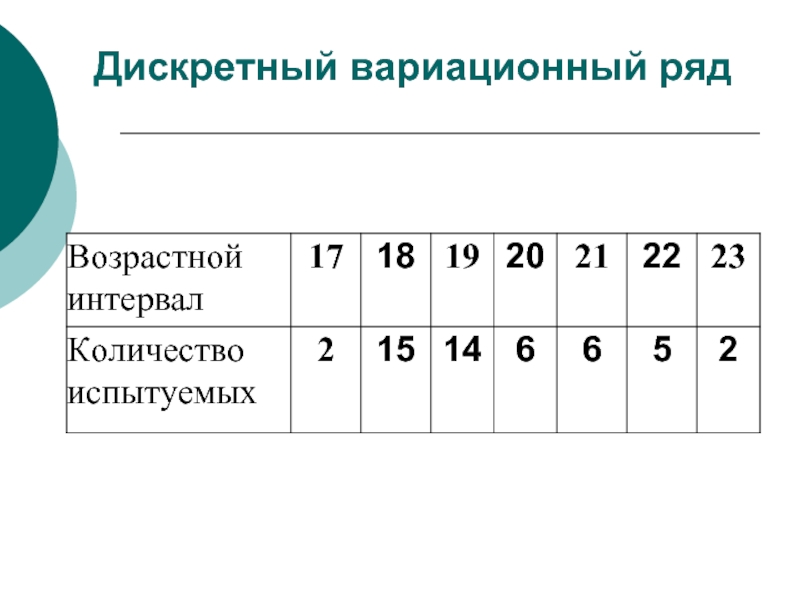
- 9. Дискретный вариационный ряд
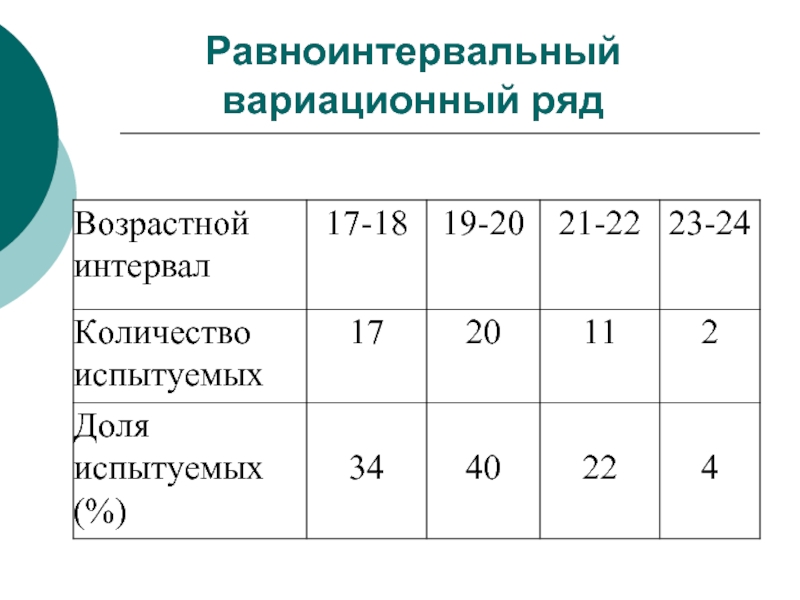
- 10. Равноинтервальный вариационный ряд
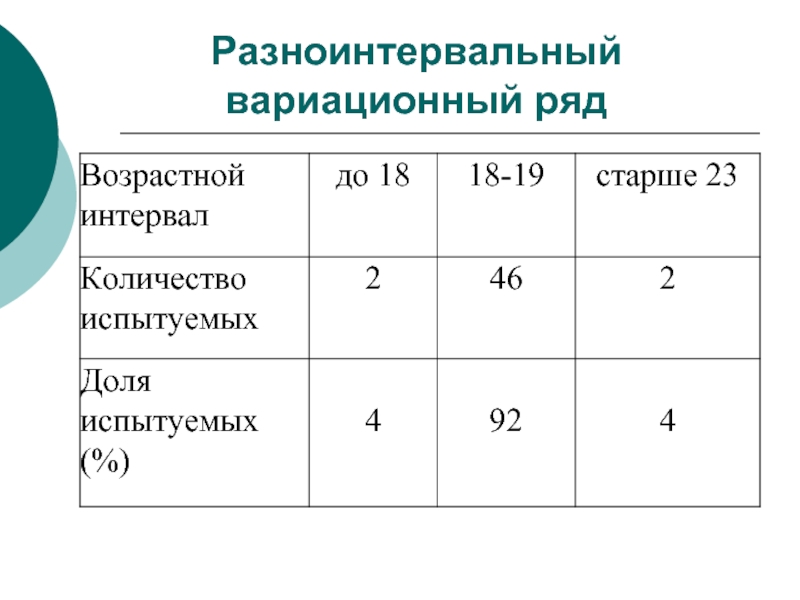
- 11. Разноинтервальный вариационный ряд
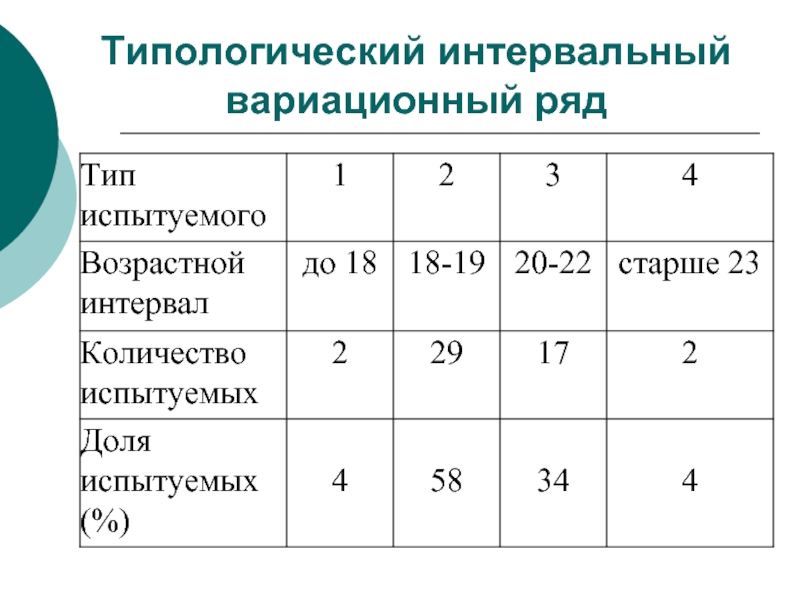
- 12. Типологический интервальный вариационный ряд
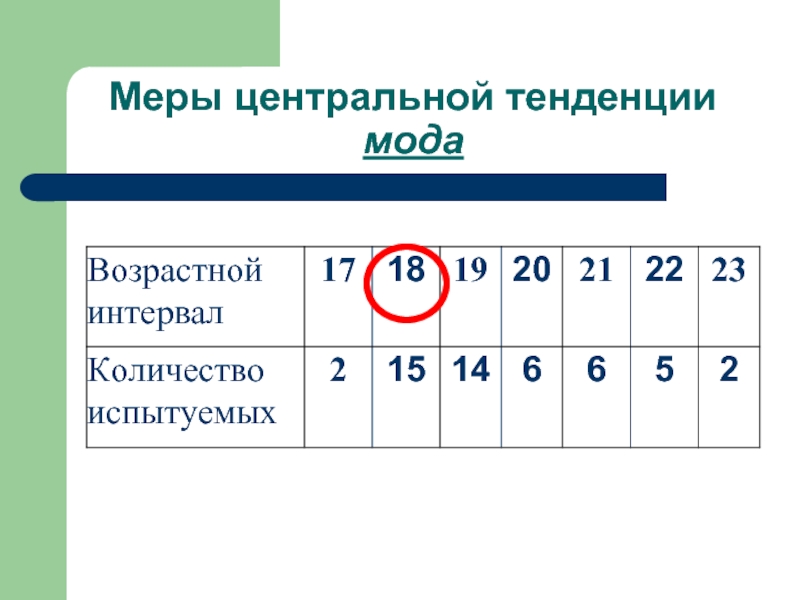
- 13. Меры центральной тенденции мода
- 14. Меры центральной тенденции медиана 100 90 80
- 15. Меры центральной тенденции средняя арифметическая величина
- 16. Меры рассеяния размах вариации 1-ое распределение:
- 17. Меры рассеяния среднее арифметическое отклонение
- 18. Меры рассеяния дисперсия D =
- 19. Меры рассеяния стандартное (среднее квадратическое) отклонение
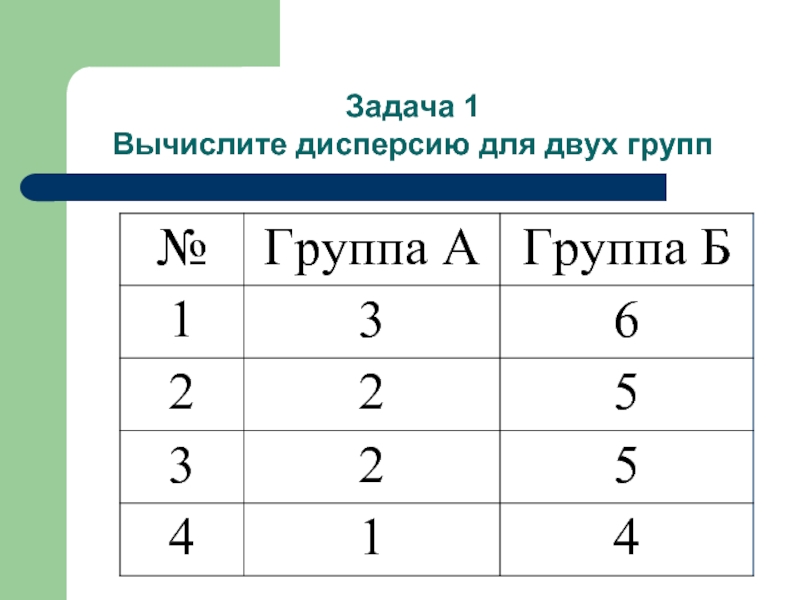
- 20. Задача 1 Вычислите дисперсию для двух групп
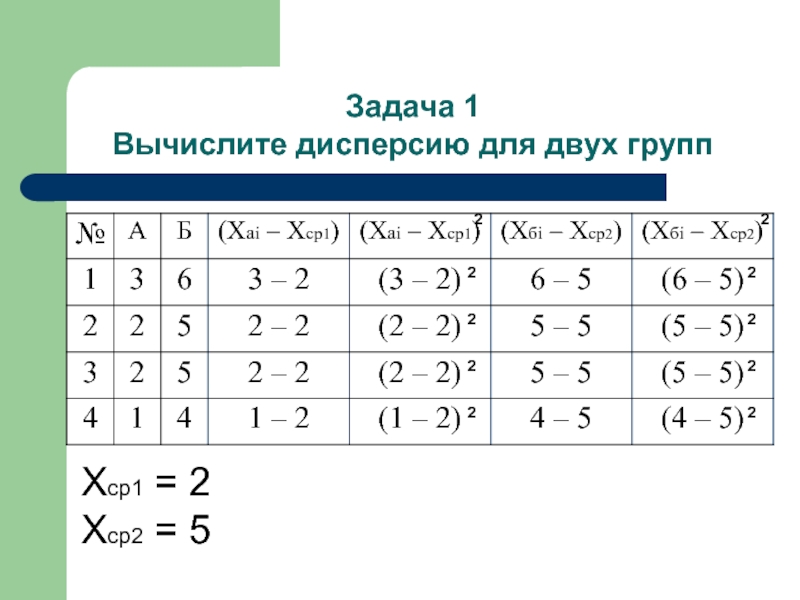
- 21. Задача 1 Вычислите дисперсию для двух групп
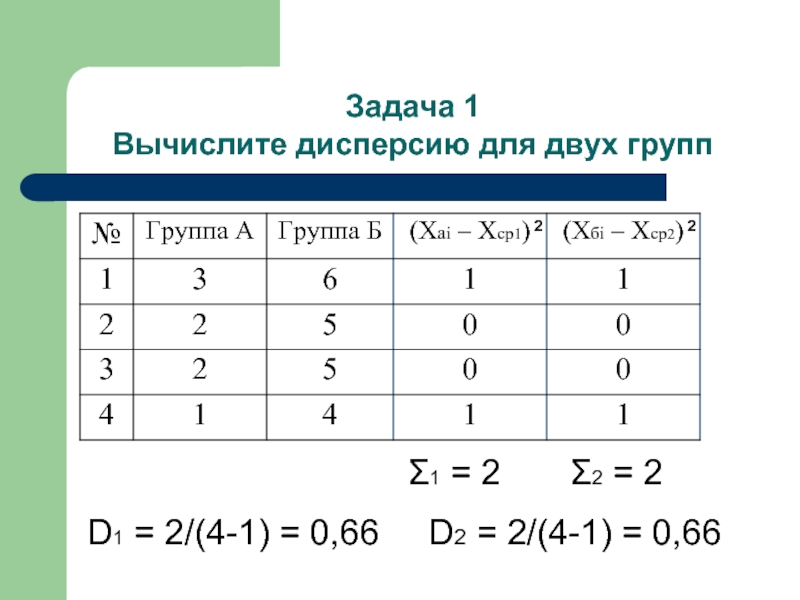
- 22. Задача 1 Вычислите дисперсию для двух групп
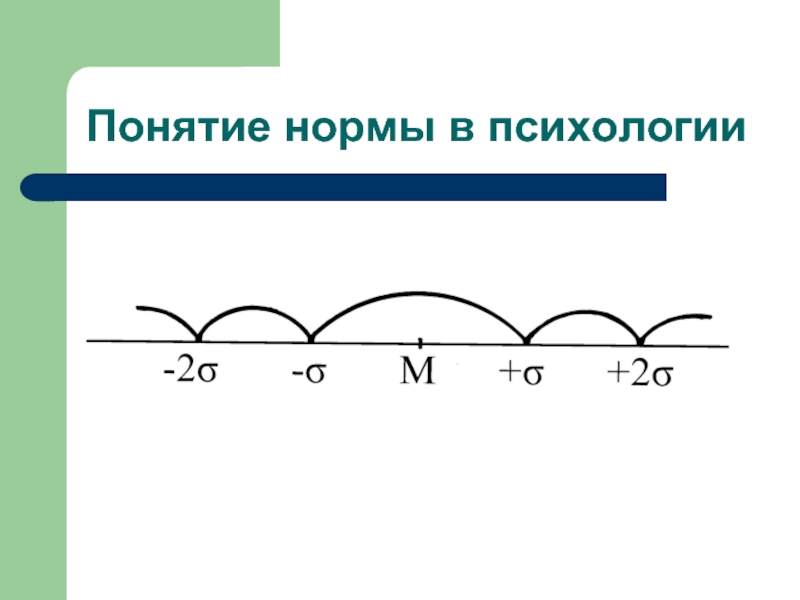
- 23. Понятие нормы в психологии
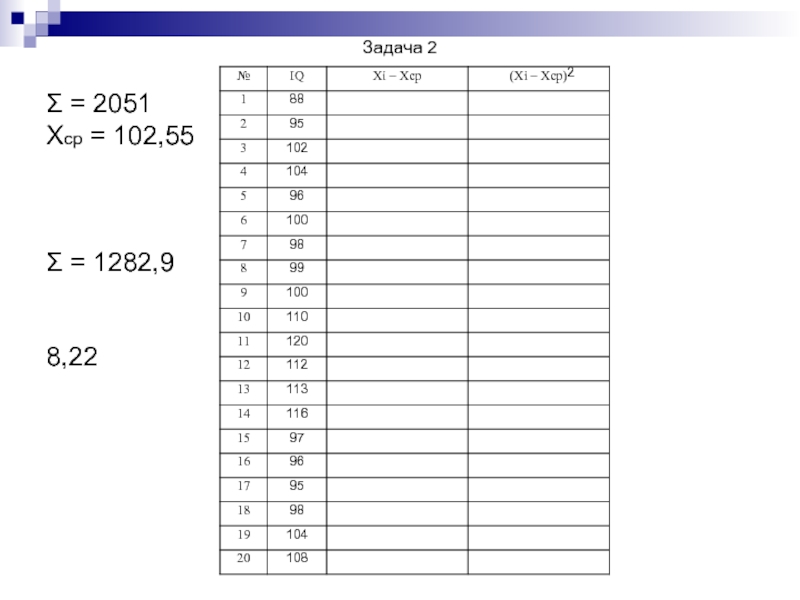
- 24. Задача 2 2 Σ = 2051 Хср
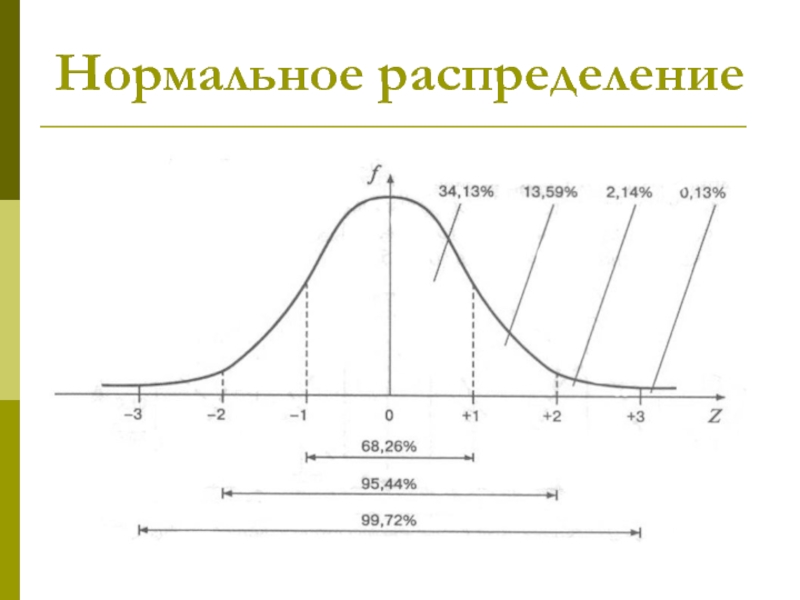
- 25. Доверительный интервал 90% 95%
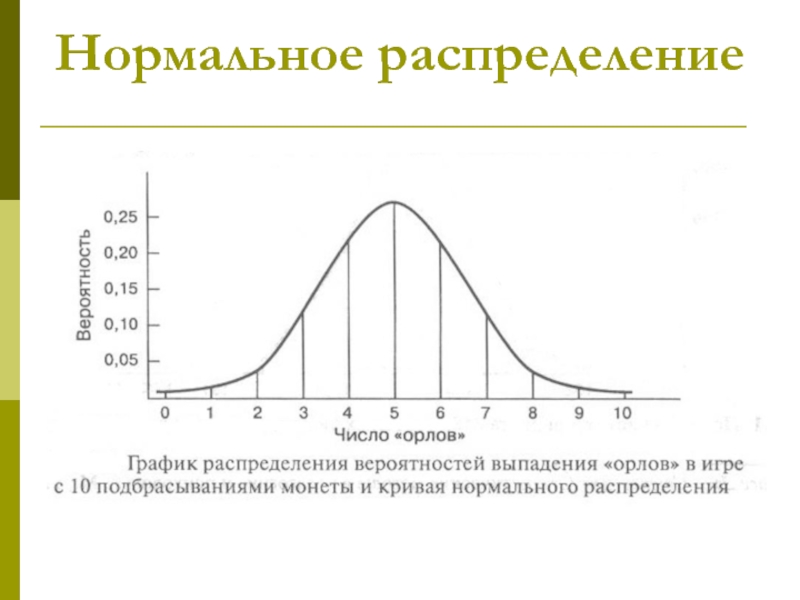
- 26. Нормальное распределение
- 27. Нормальное распределение
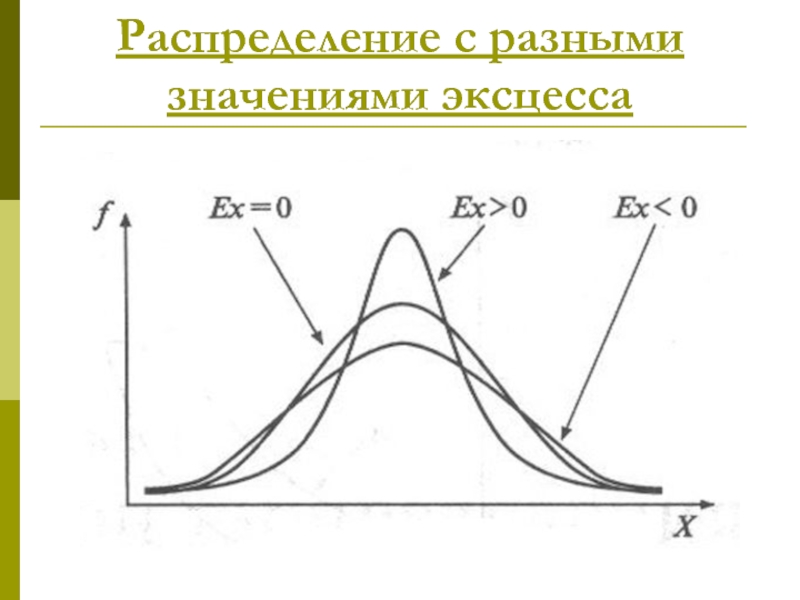
- 28. Распределение с разными значениями эксцесса
- 29. Формула для расчета эксцесса
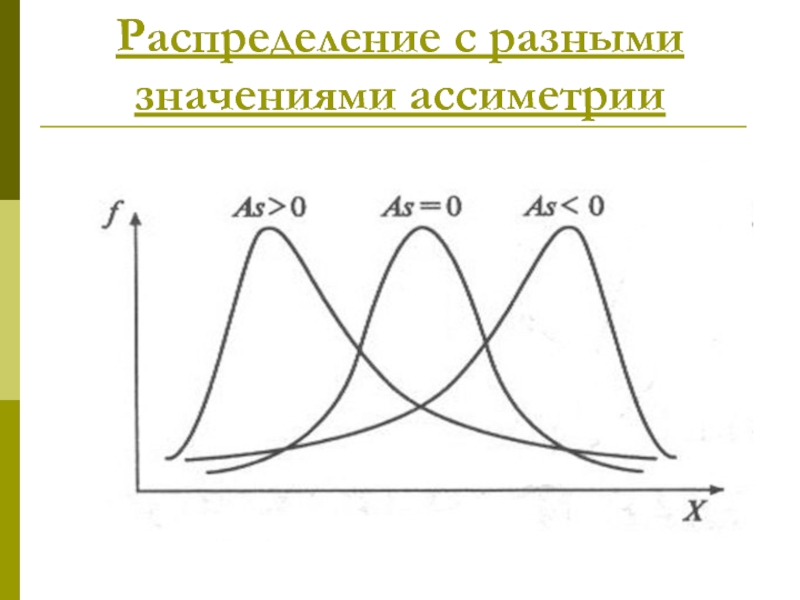
- 30. Распределение с разными значениями ассиметрии
- 31. Формула для расчета ассиметрии
- 32. Гипотеза и контргипотеза Гипотеза – это предположение,
- 33. Статистические критерии Параметрические Непараметрические
- 34. Угловое преобразование Фишера φ1 –
- 35. t-критерий Стьюдента _ Х1 – среднее
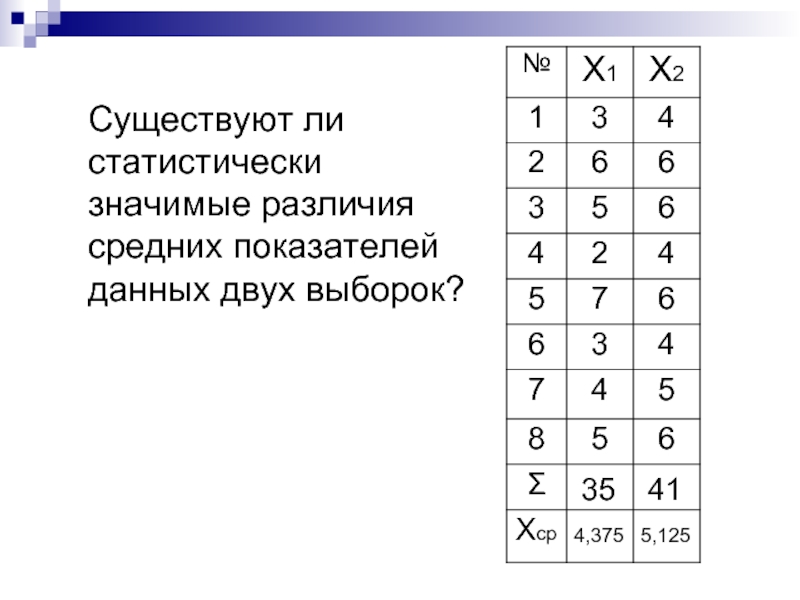
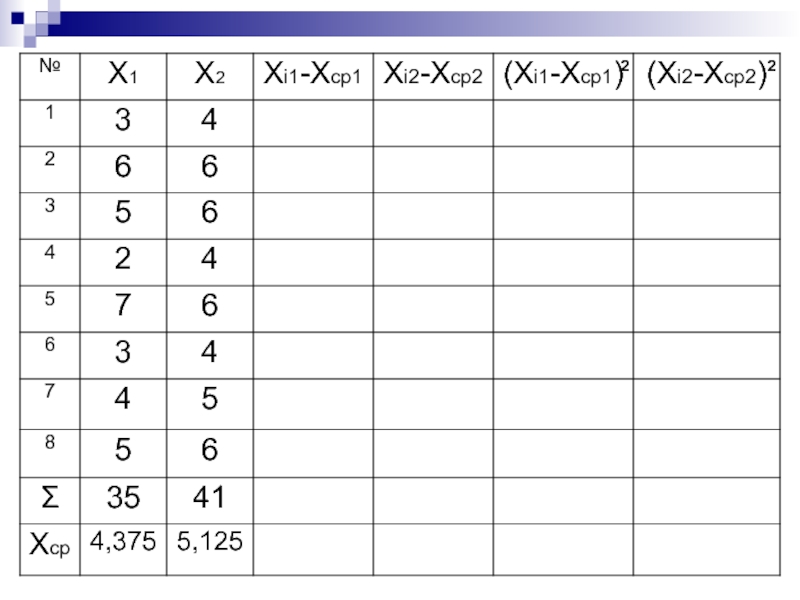
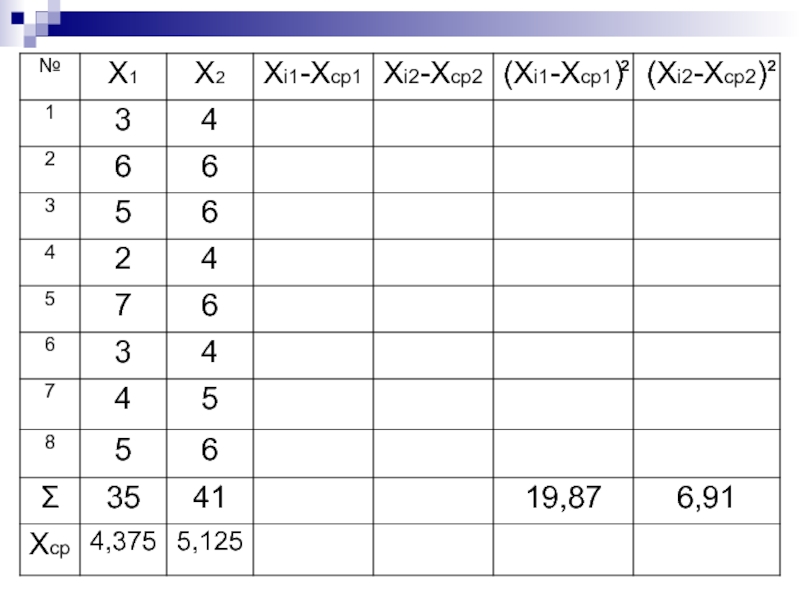
- 36. Существуют ли статистически значимые различия средних показателей данных двух выборок? 35 41 4,375 5,125
- 37. 2 2
- 38. 2 2
- 39. σ2 = 0,994 σ1
- 40. df = n1 + n2 - 2
- 41. КОРРЕЛЯЦИОННОЕ ИССЛЕДОВАНИЕ Примеры распределения испытуемых в пространстве
- 42. КОРРЕЛЯЦИОННОЕ ИССЛЕДОВАНИЕ Примеры распределения испытуемых в пространстве
- 43. КОРРЕЛЯЦИОННОЕ ИССЛЕДОВАНИЕ Примеры распределения испытуемых в пространстве 2-х признаков Нелинейная корреляция
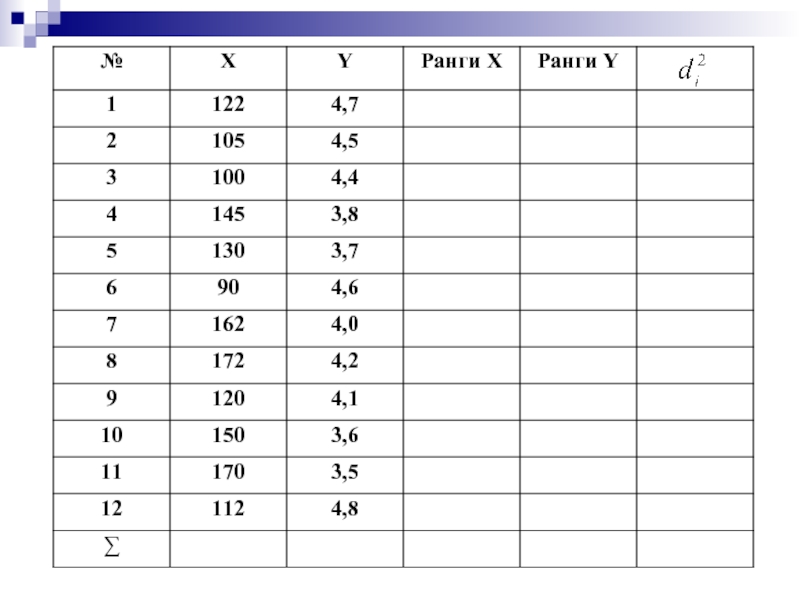
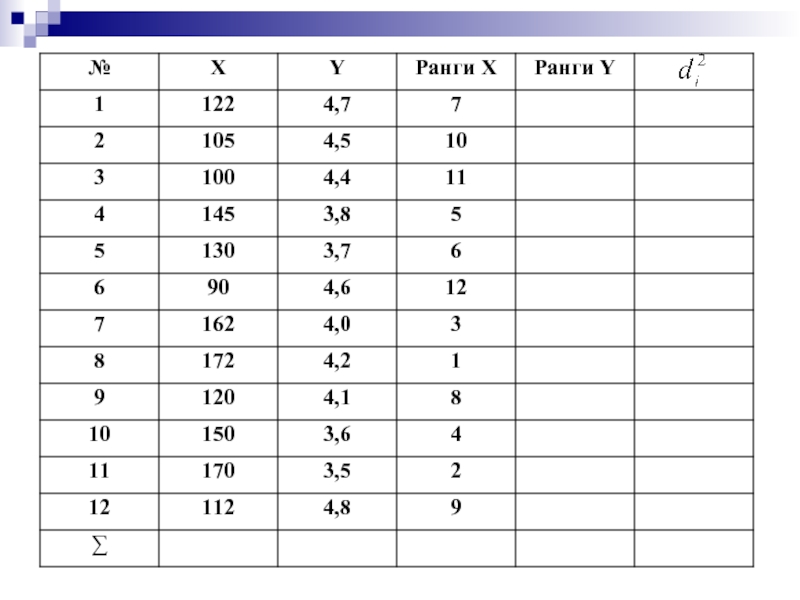
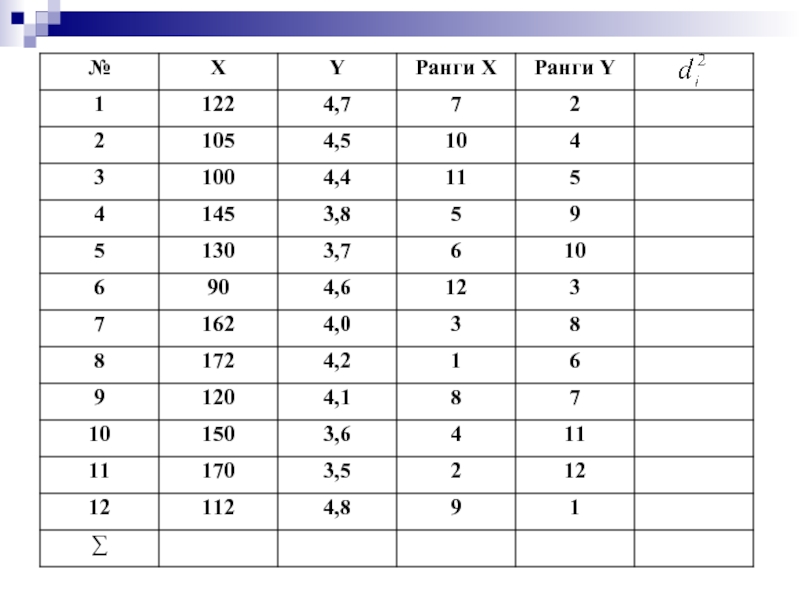
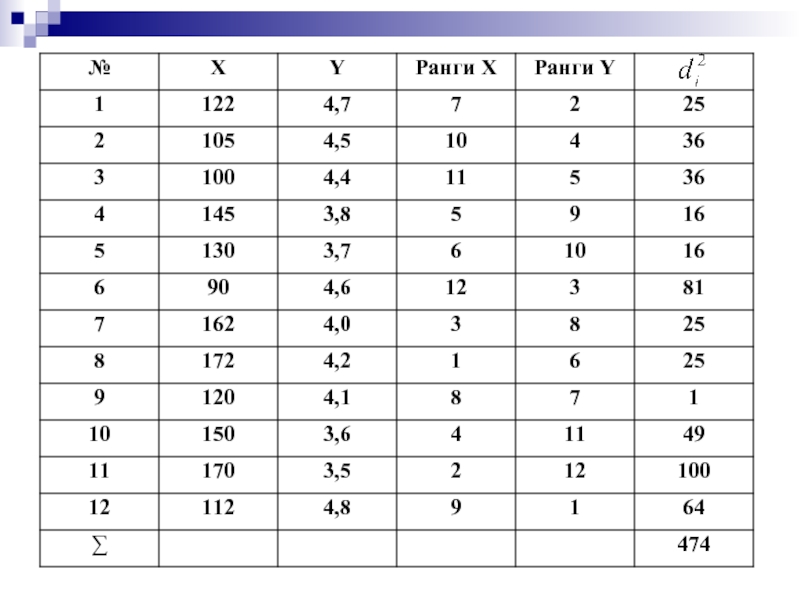
- 44. Коэффициент ранговой корреляции Спирмена d – разность
- 49. r 6х474 12х(12 – 1) = 1 2 = – 0,657
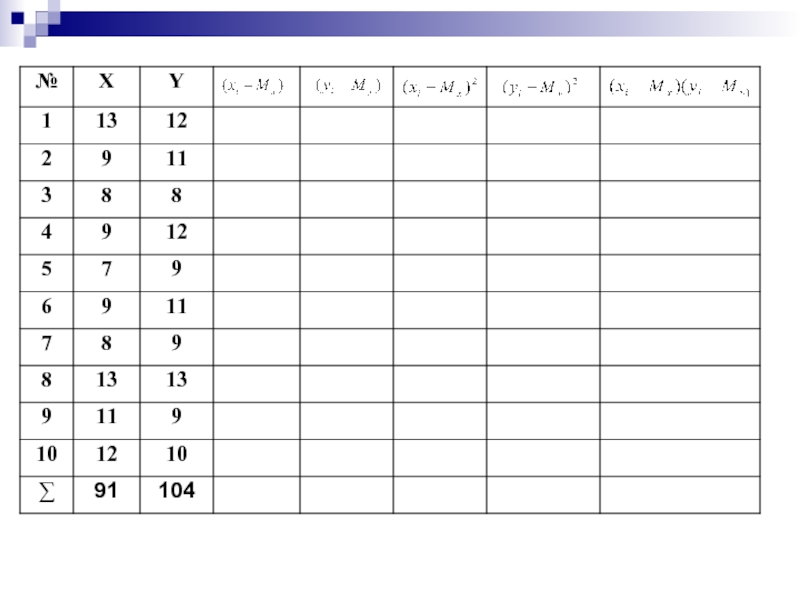
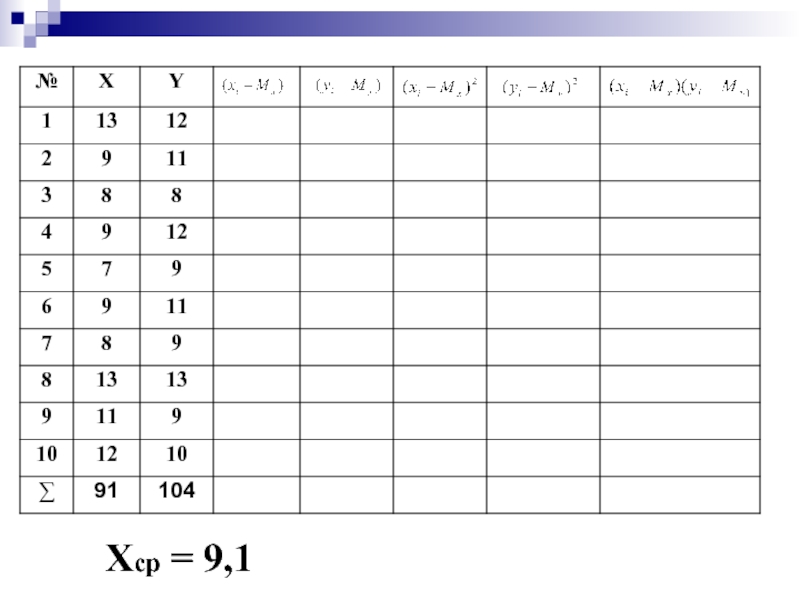
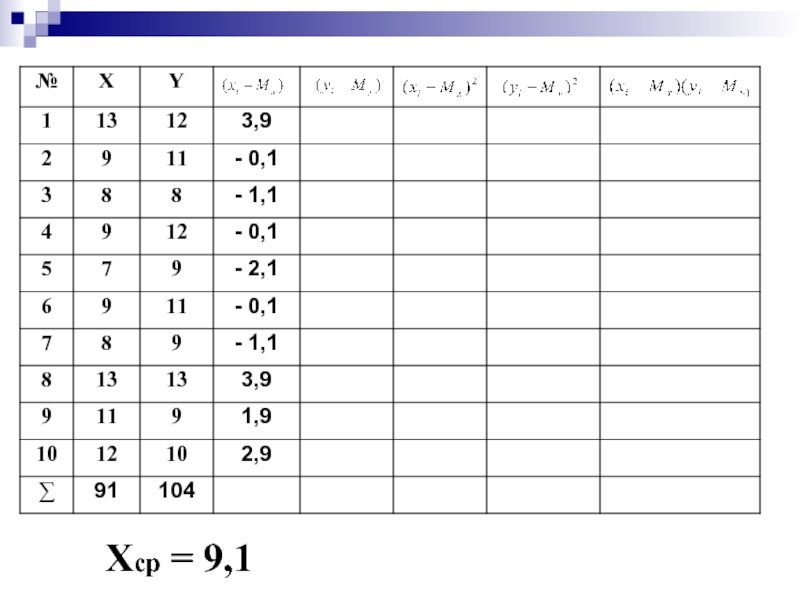
- 51. Коэффициент корреляции Бравэ – Пирсона
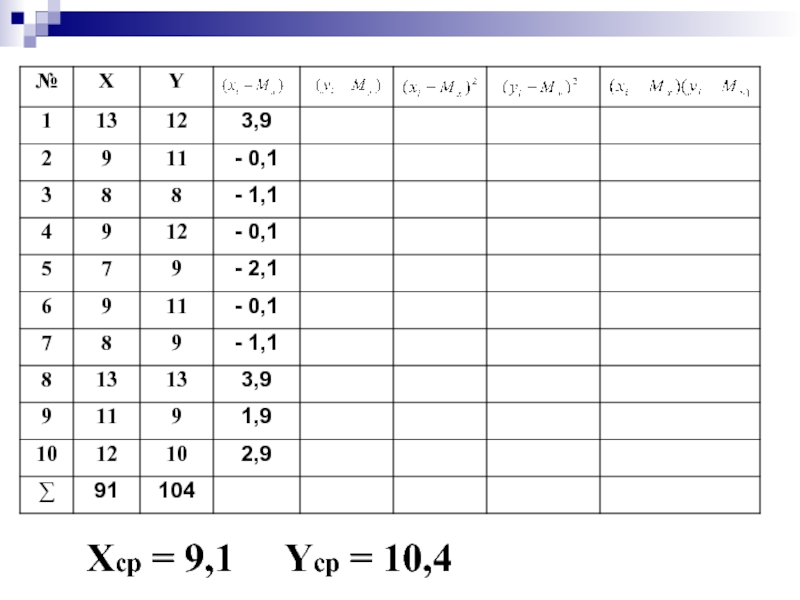
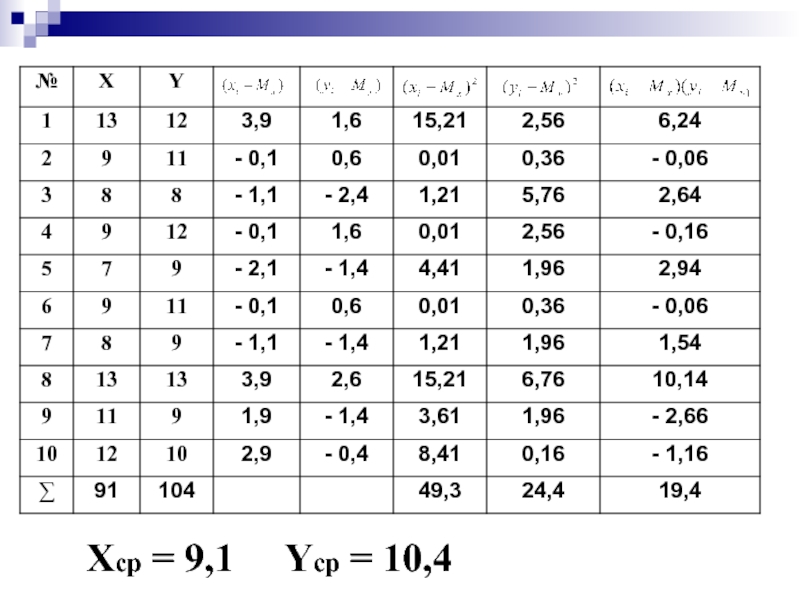
- 53. Хср = 9,1
- 54. Хср = 9,1
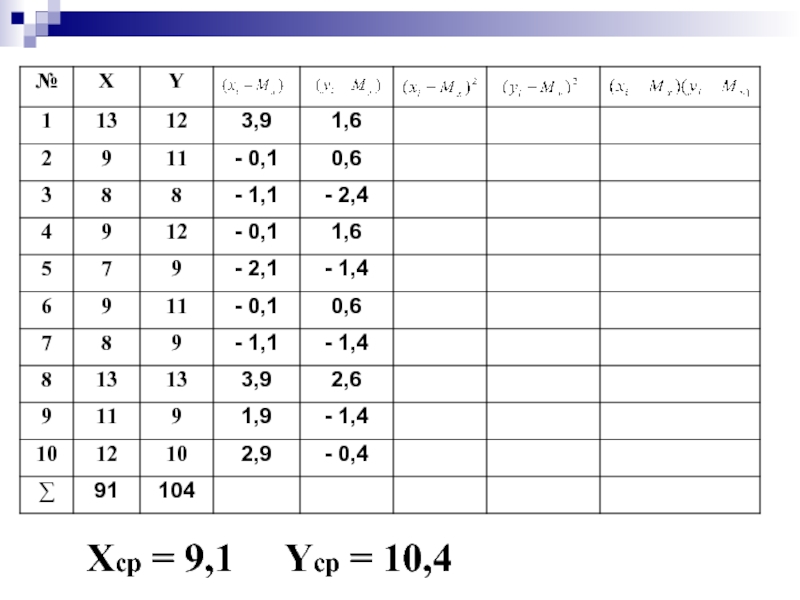
- 55. Хср = 9,1 Yср = 10,4
- 56. Хср = 9,1 Yср = 10,4
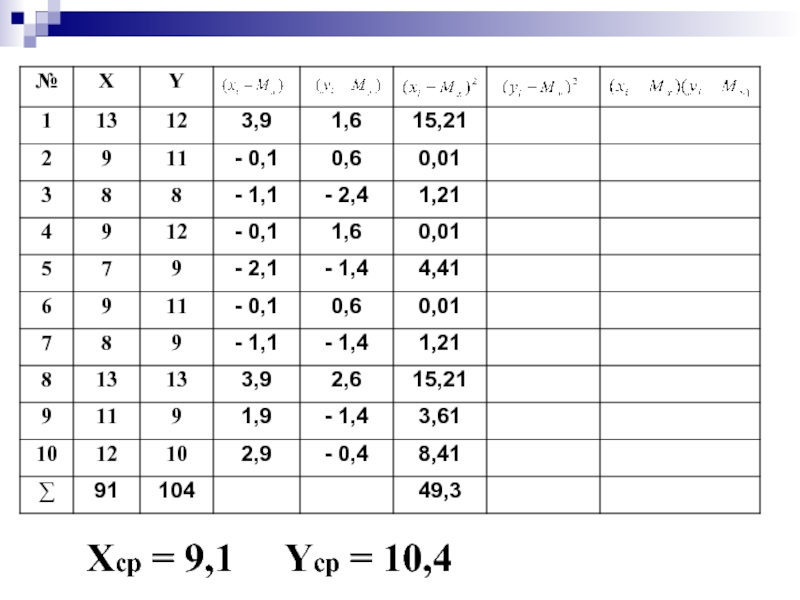
- 57. Хср = 9,1 Yср = 10,4
- 58. Хср = 9,1 Yср = 10,4
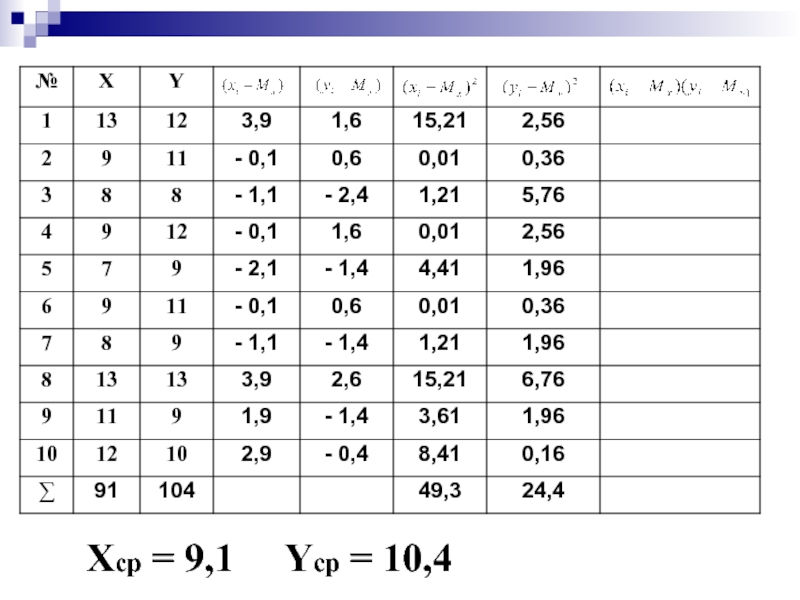
- 59. Хср = 9,1 Yср = 10,4
- 60. σ2 = 1,647 σ1
Слайд 2ИЗМЕРЕНИЕ И ШКАЛЫ
ШКАЛА НАИМЕНОВАНИЙ
ШКАЛА ПОРЯДКА
ШКАЛА ИНТЕРВАЛОВ
ШКАЛА ОТНОШЕНИЙ
ВИДЫ ИЗМЕРЕНИЙ
НОРМАТИВНОЕ
КРИТЕРИАЛЬНОЕ
ИПСАТИВНОЕ
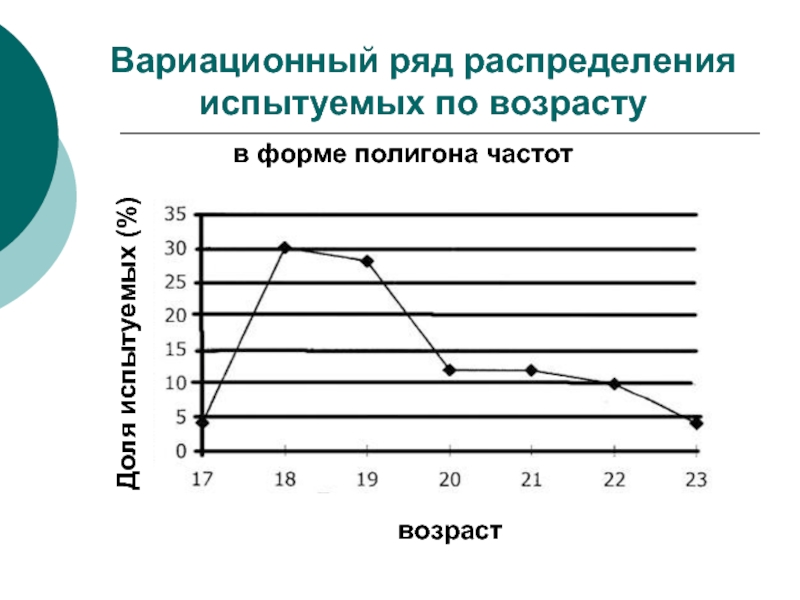
Слайд 7Вариационный ряд распределения испытуемых по возрасту
в форме полигона частот
возраст
Доля испытуемых
(%)
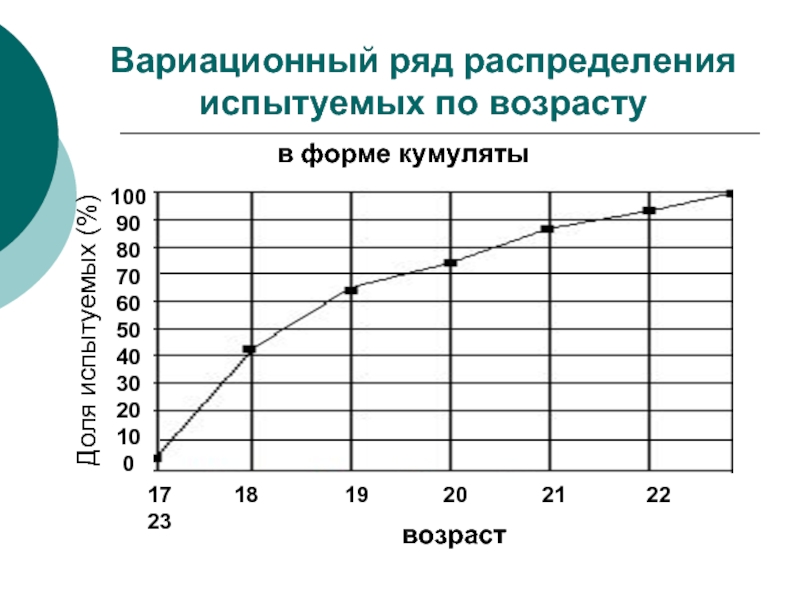
Слайд 8Вариационный ряд распределения испытуемых по возрасту
в форме кумуляты
100
90
80
70
60
50
40
30
20
10
0
17
18 19 20 21 22 23
возраст
Доля испытуемых (%)
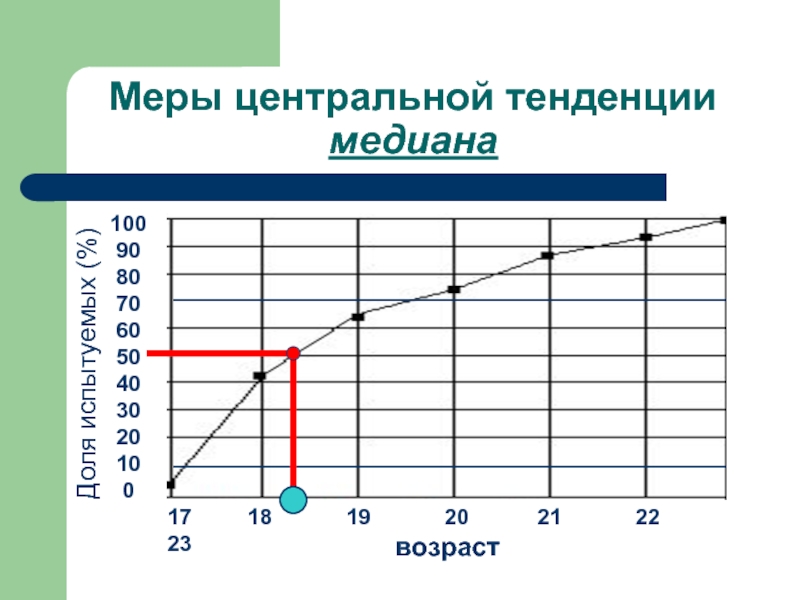
Слайд 14Меры центральной тенденции
медиана
100
90
80
70
60
50
40
30
20
10
0
17 18
19 20 21 22 23
возраст
Доля испытуемых (%)
Слайд 16Меры рассеяния
размах вариации
1-ое распределение: 31 32 36 40 41
2-ое распределение: 14
15 15 66 70
Хср = 36
R = Xmax – Xmin
Слайд 22Задача 1
Вычислите дисперсию для двух групп
2
2
Σ1 = 2
Σ2 = 2
D1 = 2/(4-1) = 0,66 D2 = 2/(4-1) = 0,66
Слайд 32Гипотеза и контргипотеза
Гипотеза – это предположение, выдвигаемое для объяснения некоторых фактов,
явлений, процессов, которые необходимо подтвердить или опровергнуть
Статистические гипотезы подразделяются на:
Нулевые (Н0) – гипотеза об отсутствии различий; или об отсутствии взаимосвязи
Альтернативные (Н1) – контргипотеза о значимости различий; или о наличии взаимосвязи
Статистические гипотезы подразделяются на:
Нулевые (Н0) – гипотеза об отсутствии различий; или об отсутствии взаимосвязи
Альтернативные (Н1) – контргипотеза о значимости различий; или о наличии взаимосвязи
Слайд 34Угловое преобразование Фишера φ1 – угол, соответствующий большей процентной доле φ2 –
угол, соответствующий меньшей процентной доле
n1 – количество наблюдений в выборке 1
n2 – количество наблюдений в выборке 2
φ*= (φ1 – φ2)
Слайд 35t-критерий Стьюдента
_
Х1 – среднее значение переменной по одной выборке данных
_
Х2 –
среднее значение переменной по другой выборке данных
n1 – число частных значений переменной по первой выборке
n2 – число частных значений переменной по второй выборке
σ1 и σ2 – показатели отклонений частных значений из двух сравниваемых выборок от соответствующих им средних величин
n1 – число частных значений переменной по первой выборке
n2 – число частных значений переменной по второй выборке
σ1 и σ2 – показатели отклонений частных значений из двух сравниваемых выборок от соответствующих им средних величин
tэмп =
Хср1 – Хср2
σ
σ
n1
n2
+
2
2
Слайд 36Существуют ли статистически
значимые различия средних показателей
данных двух выборок?
35
41
4,375
5,125
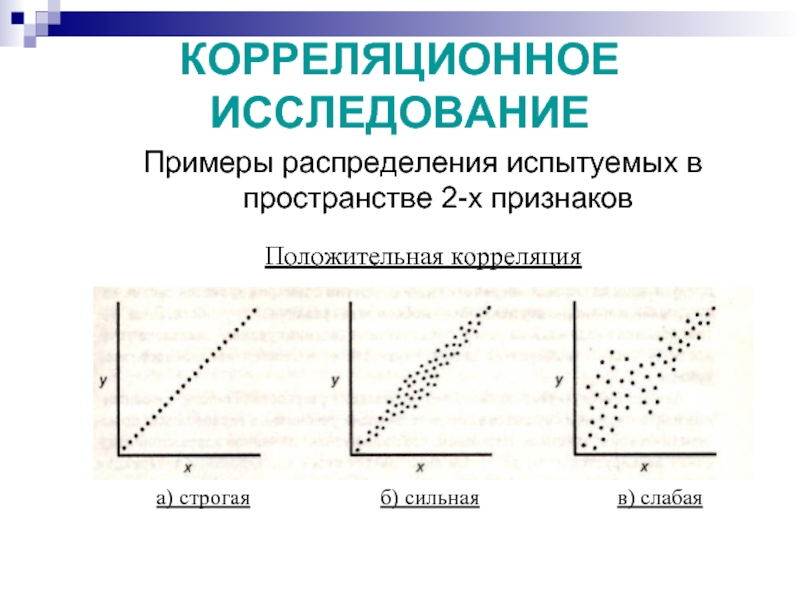
Слайд 41КОРРЕЛЯЦИОННОЕ ИССЛЕДОВАНИЕ
Примеры распределения испытуемых в пространстве 2-х признаков
Положительная корреляция
а) строгая
б) сильная
в)
слабая
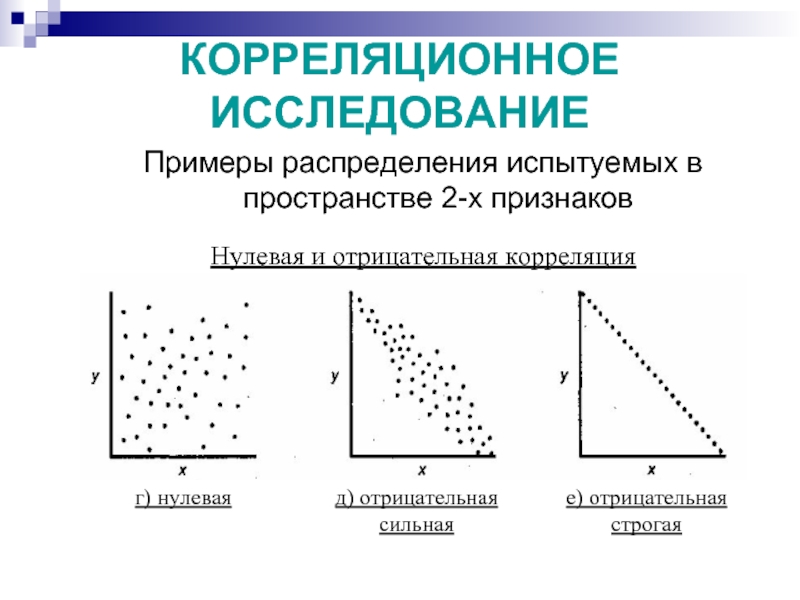
Слайд 42КОРРЕЛЯЦИОННОЕ ИССЛЕДОВАНИЕ
Примеры распределения испытуемых в пространстве 2-х признаков
Нулевая и отрицательная корреляция
г)
нулевая
д) отрицательная сильная
е) отрицательная строгая
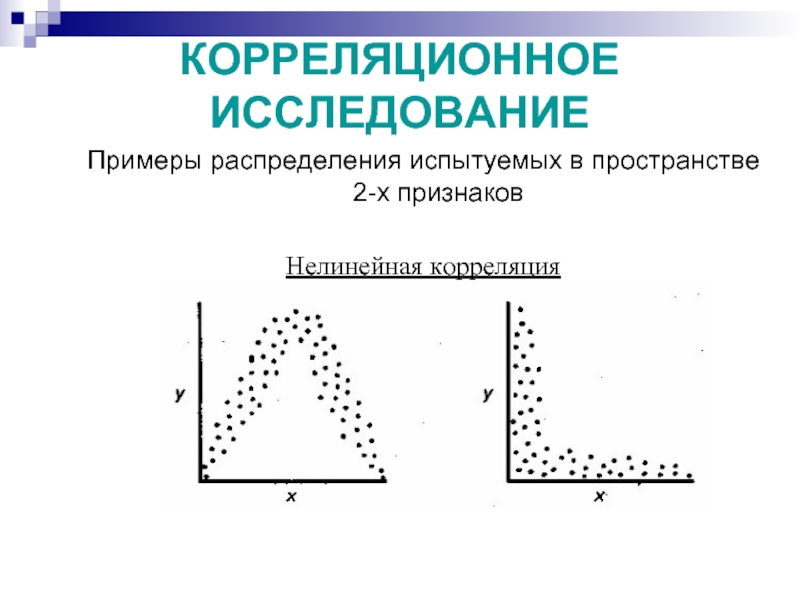
Слайд 43КОРРЕЛЯЦИОННОЕ ИССЛЕДОВАНИЕ
Примеры распределения испытуемых в пространстве 2-х признаков
Нелинейная корреляция
Слайд 44Коэффициент ранговой корреляции Спирмена
d – разность между рангами по двум переменным
для каждого испытуемого
N – количество ранжируемых значений
N – количество ранжируемых значений
