- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Второй и третий признаки подобия треугольников презентация
Содержание
- 1. Второй и третий признаки подобия треугольников
- 2. II признак подобия треугольников. Если две стороны
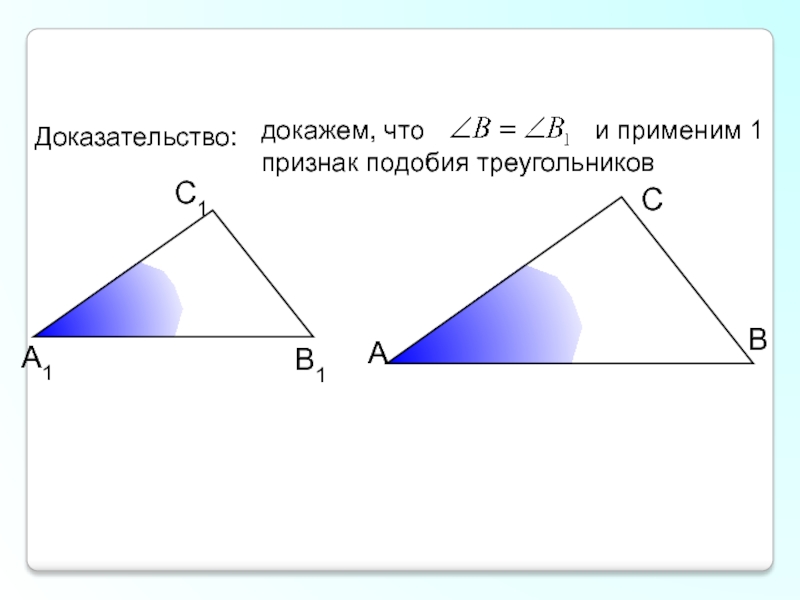
- 3. Идея доказательства: Рассмотрим два треугольника ABC и
- 4. докажем, что
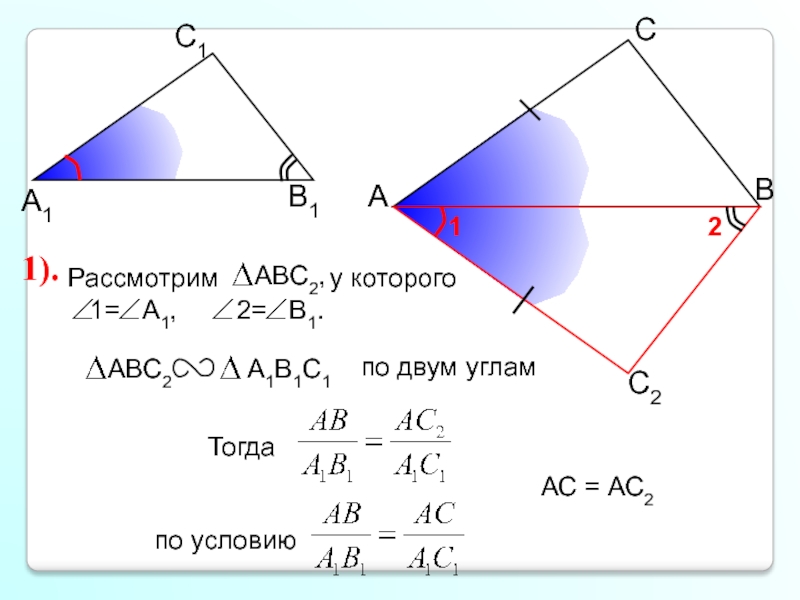
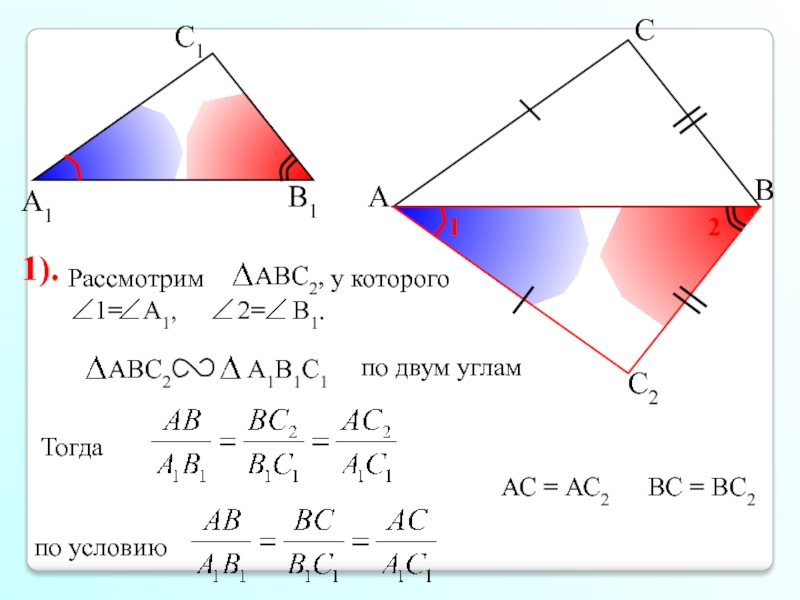
- 5. А С В В1 С1 А1 АС = АС2 1).
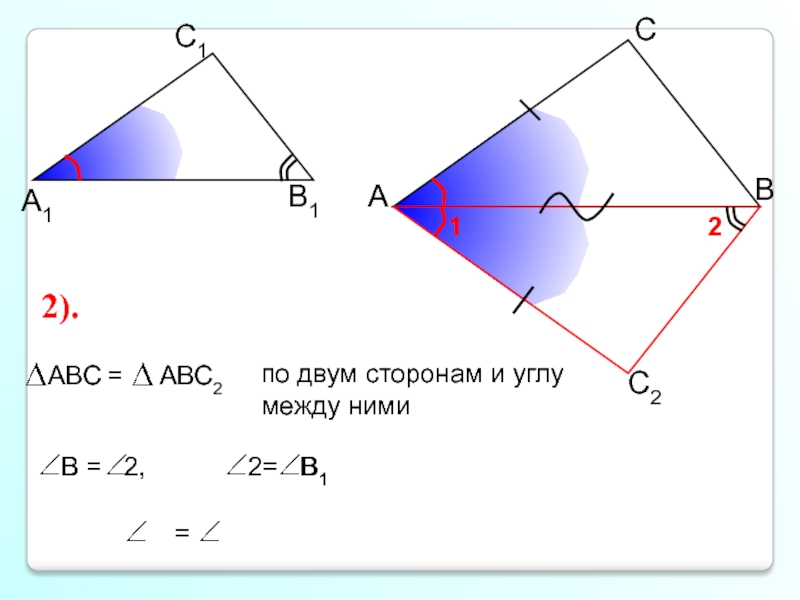
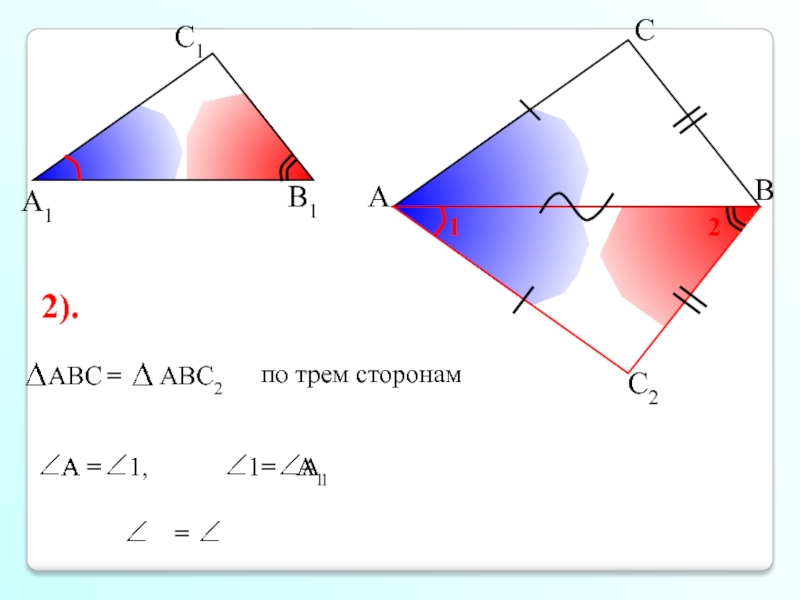
- 6. А С В В1 С1 А1 2). В1 В
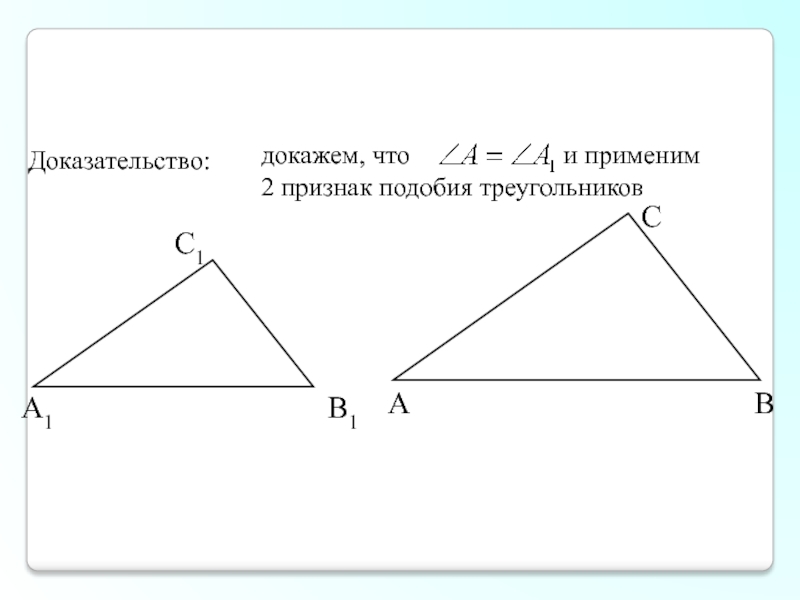
- 7. III признак подобия треугольников. Если три стороны
- 8. Доказательство: (аналогично) Что нужно рассмотреть, чтобы
- 9. докажем, что
- 10. А С В В1 С1 А1
- 11. А1 А А С В В1 С1 А1 2).
- 12. Решение задач
- 13. По данным рисунка Найти: x Доказать:
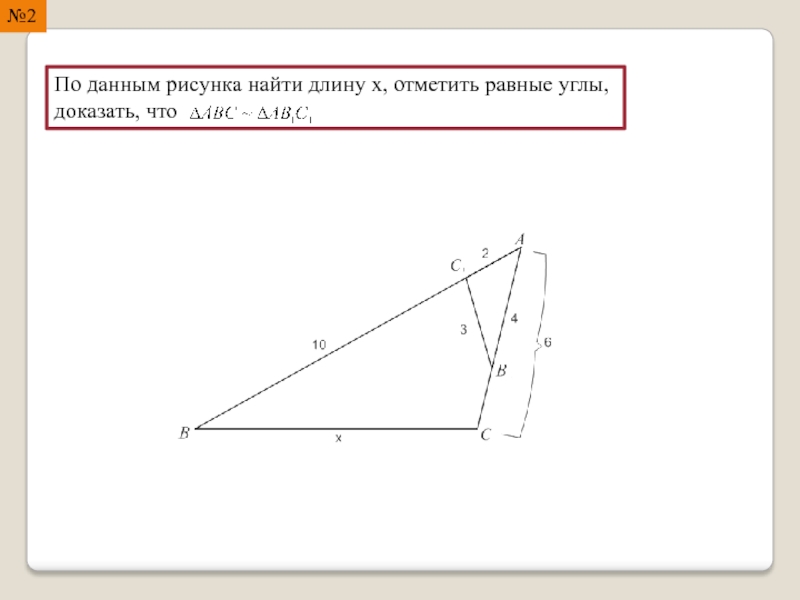
- 14. №2 По данным рисунка найти длину x, отметить равные углы, доказать, что
- 15. №3 Подобны ли треугольники ABC и А1В1С1,
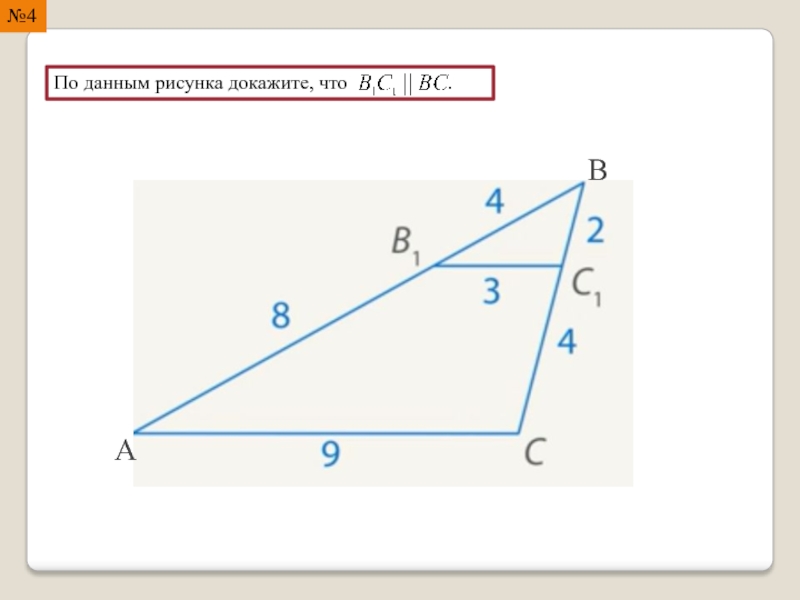
- 16. По данным рисунка докажите, что
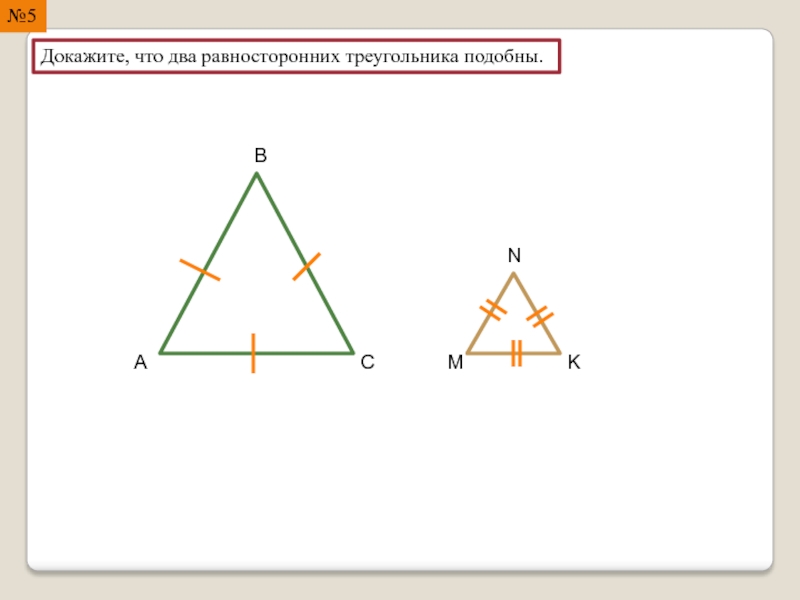
- 17. №5 Докажите, что два равносторонних треугольника подобны. M A B C N K
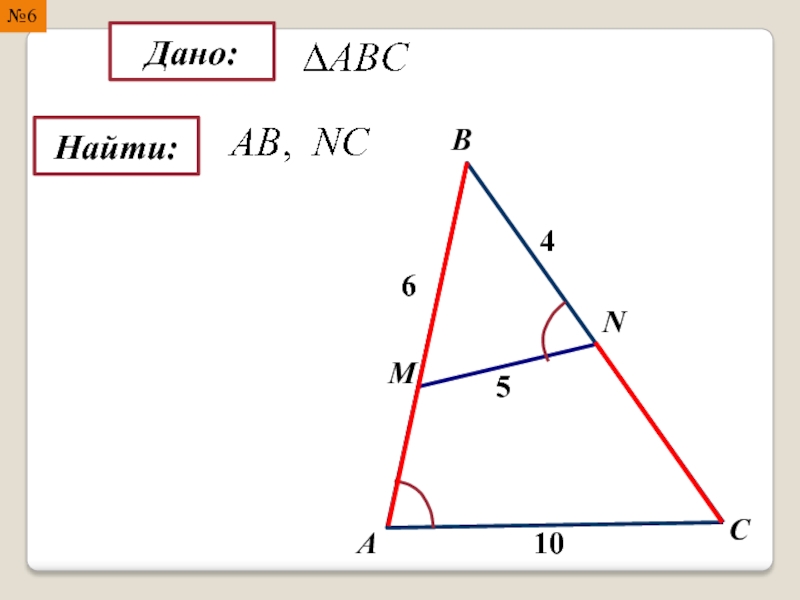
- 18. Найти: Дано: А B C M
- 19. Домашняя работа: из презентации задачи №2, 3,
Слайд 2II признак подобия треугольников. Если две стороны одного треугольника пропорциональны двум
Слайд 3Идея доказательства: Рассмотрим два треугольника ABC и
Докажем, что они подобны. Для этого построим треугольник и докажем, что он подобен треугольнику . Рассмотрим треугольники
ABC и и докажем, что они равны. Сделаем вывод о подобии треугольников ABC и .
Слайд 7III признак подобия треугольников. Если три стороны одного треугольника пропорциональны трем
Слайд 8Доказательство: (аналогично)
Что нужно рассмотреть, чтобы доказать, что
Каким признаком подобия мы воспользуемся?
Какой вспомогательный треугольник мы должны рассмотреть?
Какому треугольнику он будет подобен? По какому признаку?
Если треугольники подобны, то какое отношение мы можем составить?
С каким отношением мы должны его сравнить? Что будет следовать?
Слайд 13По данным рисунка
Найти: x
Доказать: BC||AD
Решение:
1) Рассмотрим два треугольника с
, так как они вертикальные.
Рассмотрим отношение прилегающие стороны:
Согласно II признаку подобия ~ . Коэффициент подобия k=2.
С помощью него определим длину x=AD:
2) Так как , то все углы у них равны.
- эти углы являются
накрест лежащими при пересечении прямых BC и AD секущей BD. Таким образом,
BC||AD.
Ответ: 8
№1
Слайд 15№3
Подобны ли треугольники ABC и А1В1С1, если АВ = 3 см,
B
A
C
Слайд 19Домашняя работа: из презентации задачи №2, 3, 4, 5, 6
тетрадь-конспект стр.
стр. 55 – типовая задача, опорная задача.