- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема про три перпендикуляри презентация
Содержание
- 1. Теорема про три перпендикуляри
- 2. Відрізок АВ - перпендикуляр, точка В —
- 3. Властивості проекції 1. Перпендикуляр, проведений з даної
- 4. Відстань від точки до площини Довжина перпендикуляра,
- 5. α a A b c
- 6. α a A b c
- 7. α A
- 8. α A
- 9. α A
- 10. Дві прямі, що перетинаються, в
- 11. Нехай дано площину α і пряму а,
- 12. Якщо точка рівновіддалена від усіх вершин многокутника,
Слайд 2Відрізок АВ - перпендикуляр, точка В — основа цього перпендикуляра.
Будь-який
Перпендикуляр і похила
Слайд 3Властивості проекції
1. Перпендикуляр, проведений з даної точки до площини, менший будь-якої
2. Якщо похилі рівні, то рівні і їх проекції;
3. Якщо проекції похилих рівні, то рівні і похилі;
4. Якщо похилі не рівні, то більша похила має і більшу проекцію.
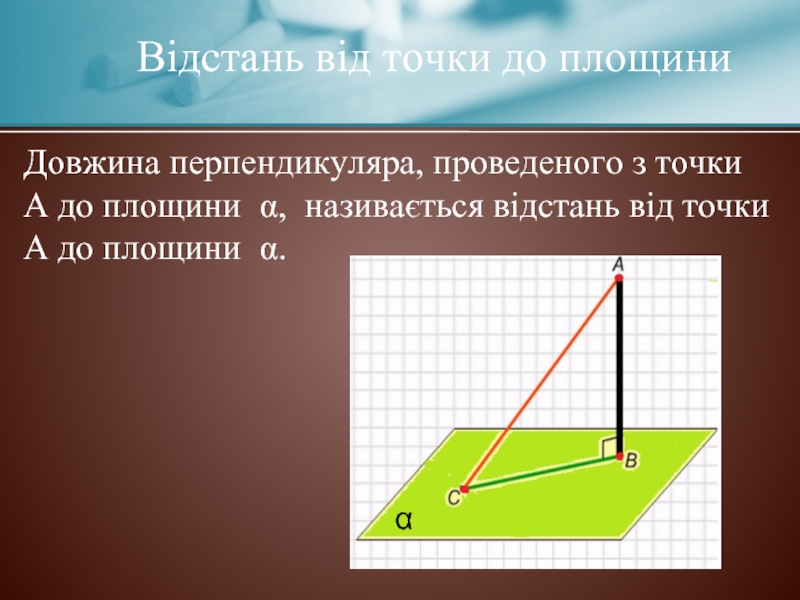
Слайд 4Відстань від точки до площини
Довжина перпендикуляра, проведеного з точки А до
α
Слайд 5
α
a
A
b
c
d
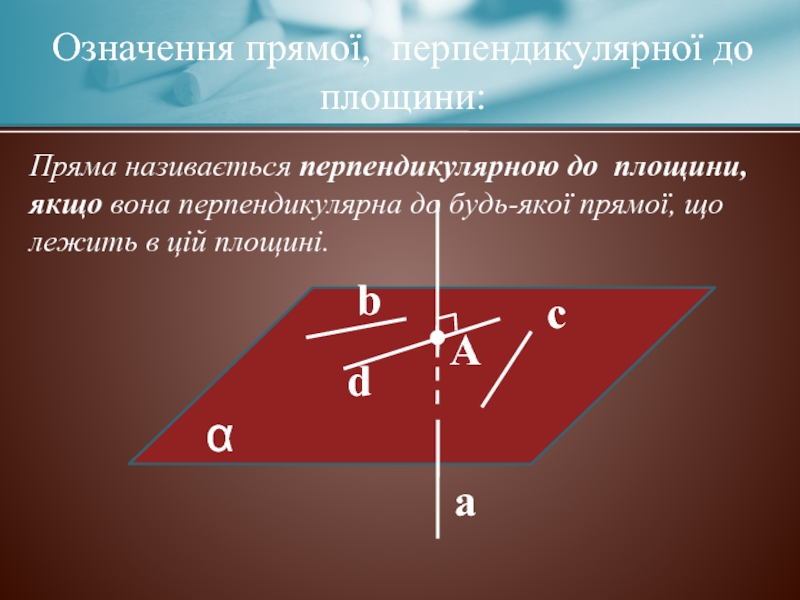
Означення прямої, перпендикулярної до площини:
Пряма називається перпендикулярною до площини, якщо
Слайд 6
α
a
A
b
c
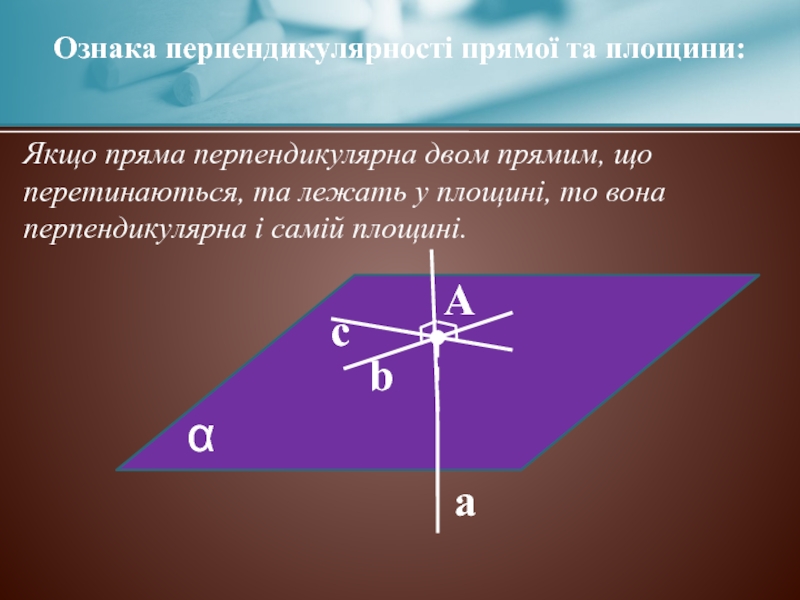
Якщо пряма перпендикулярна двом прямим, що перетинаються, та лежать у площині,
перпендикулярна і самій площині.
Ознака перпендикулярності прямої та площини:
Слайд 7
α
A
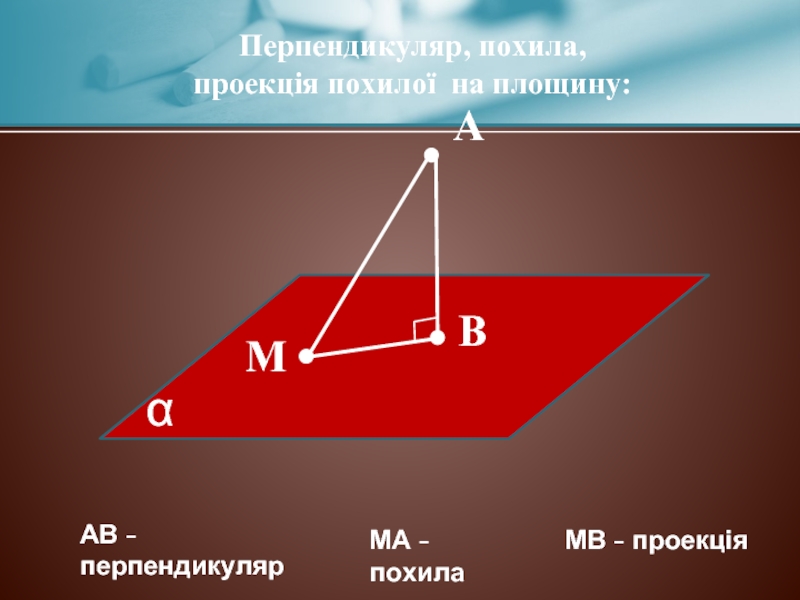
Перпендикуляр, похила,
проекція похилої на площину:
В
М
АВ - перпендикуляр
МА -
МВ - проекція
Слайд 8
α
A
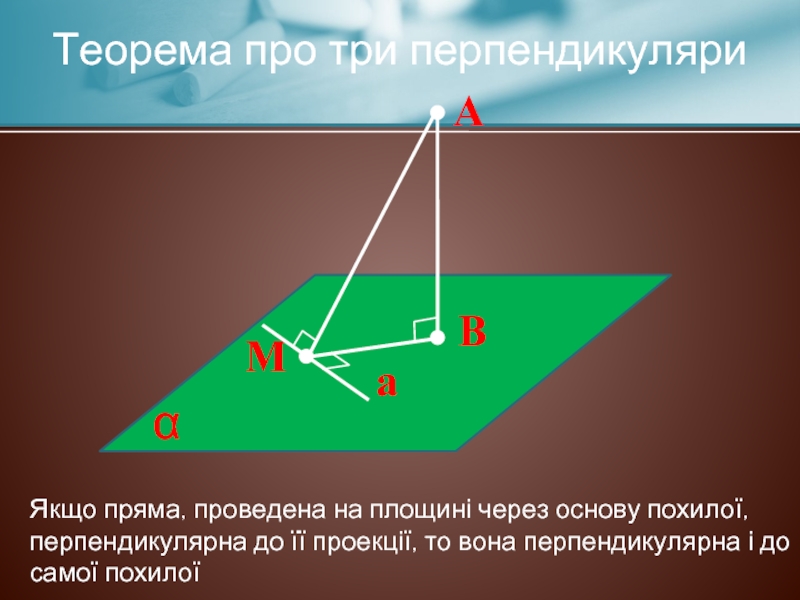
Теорема про три перпендикуляри
В
М
а
Якщо пряма, проведена на площині через
Слайд 9
α
A
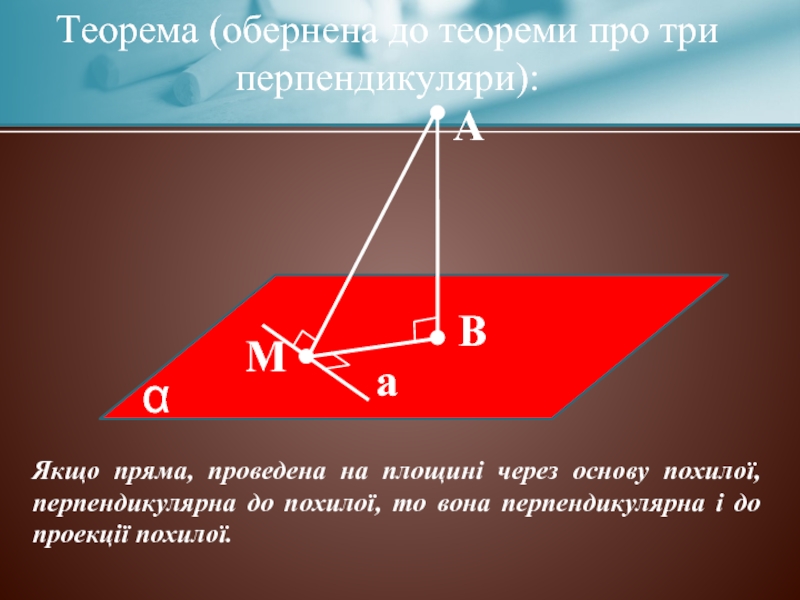
Теорема (обернена до теореми про три перпендикуляри):
В
М
а
Якщо пряма, проведена
Слайд 10
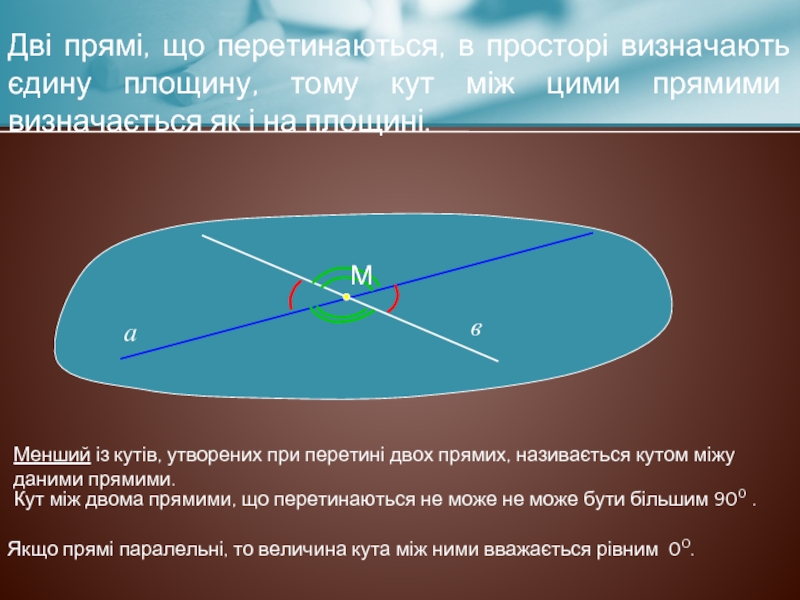
Дві прямі, що перетинаються, в просторі визначають єдину площину, тому кут
а
в
Менший із кутів, утворених при перетині двох прямих, називається кутом міжу даними прямими.
Кут між двома прямими, що перетинаються не може не може бути більшим 900 .
Якщо прямі паралельні, то величина кута між ними вважається рівним 00.
М
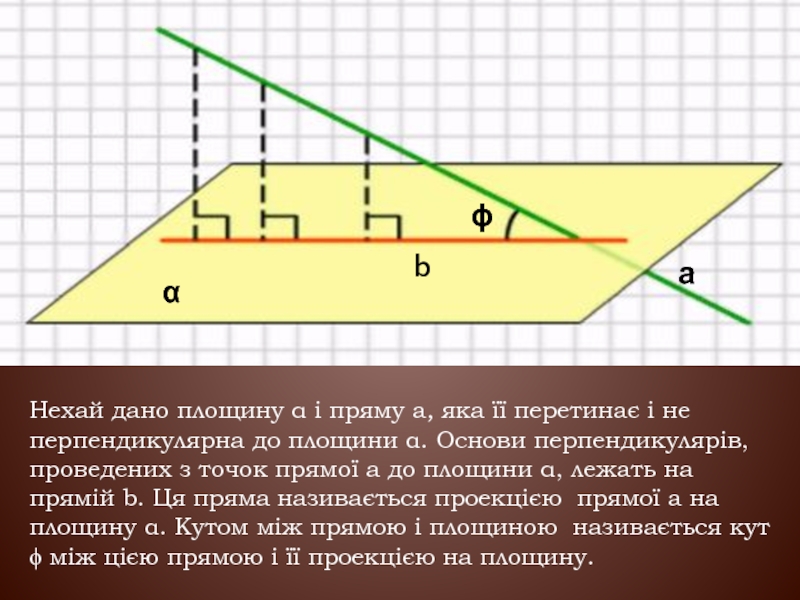
Слайд 11Нехай дано площину α і пряму а, яка її перетинає і
b
а
α
ϕ
Слайд 12Якщо точка рівновіддалена від усіх вершин многокутника, то основою перпендикуляра, опущеного
Висновок 2