- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Модели с дискретными переменными презентация
Содержание
- 1. Модели с дискретными переменными
- 2. 1. Фиктивные объясняющие переменные
- 3. Примерами таких признаков
- 4. Такие переменные приводят
- 5. где ,
- 6. Такие модели называют ANCOVA-моделями (модели ковариационного анализа).
- 7. где , если
- 8. Если рассматриваемый
- 9. В данной модели
- 10. Как видим, третьей фиктивной переменной не требуется,
- 11. 2. Модели с дискретными зависимыми переменными
- 12. Номинальные переменные.
- 13. Выбор значения осуществляется
- 14. Главная особенность приведённых
- 15. 1. Доход семьи: низкий, средний, высокий, очень
- 16. Количественные целочисленные переменные. Примерами
- 17. Для моделей с описанными
- 18. Если
- 19. Рассмотрим вначале простейшие
- 20. На решение о покупке
- 21. Выдвигая различные
- 22. Поскольку
- 23. В итоге модель (2)
- 24. может находиться вне отрезка
- 25. От указанного недостатка,
- 26. В частности, в
- 27. 2. Если в качестве
- 28. В том случае, когда номинальная зависимая
- 29. Тогда выбор одного
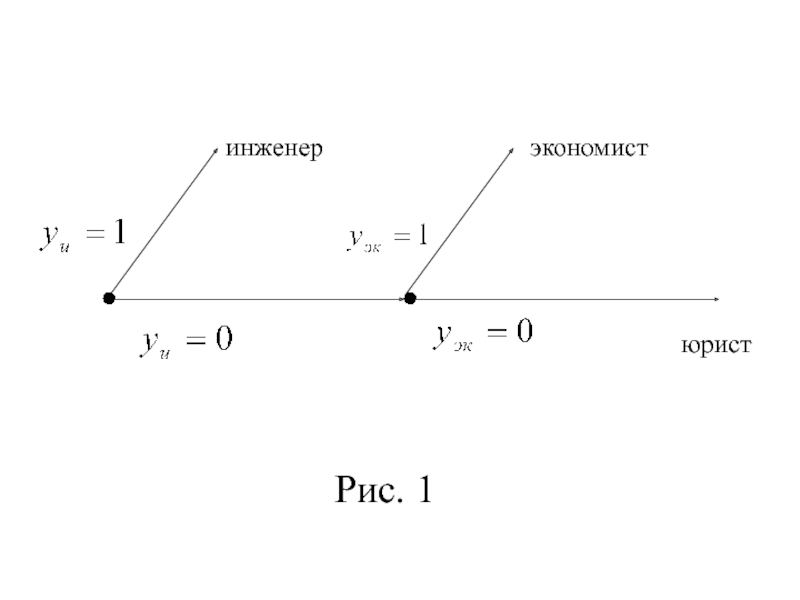
- 30. Рис. 1
- 31. 3. Тесты Гуйарати и Чоу Пусть требуется
- 32. Пусть до момента
- 33. Если же структурные
- 34. где В итоге
- 35. С помощью
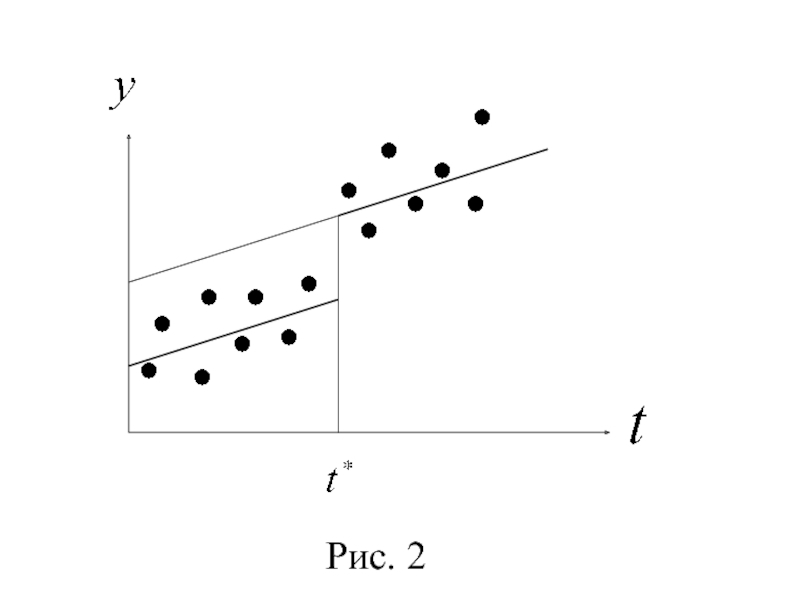
- 36. Рис. 2
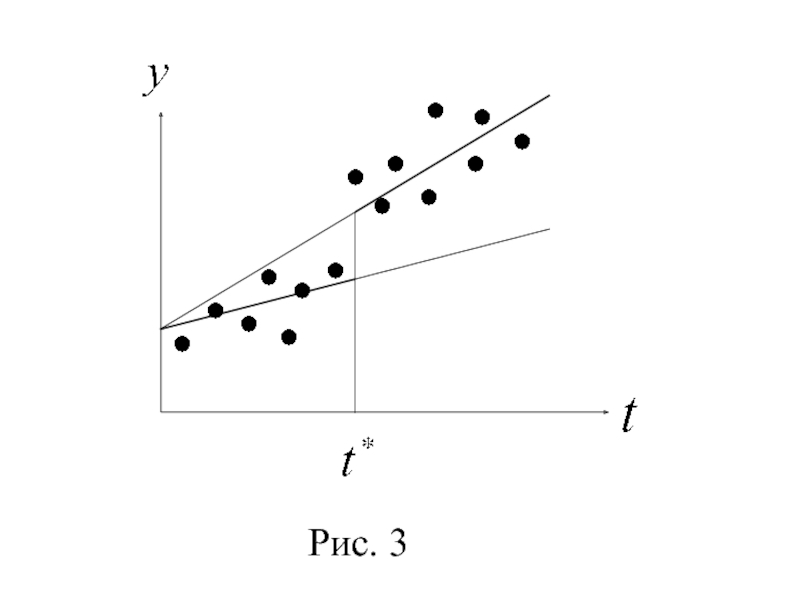
- 37. Рис. 3
- 38. 2°. Если параметр статистически
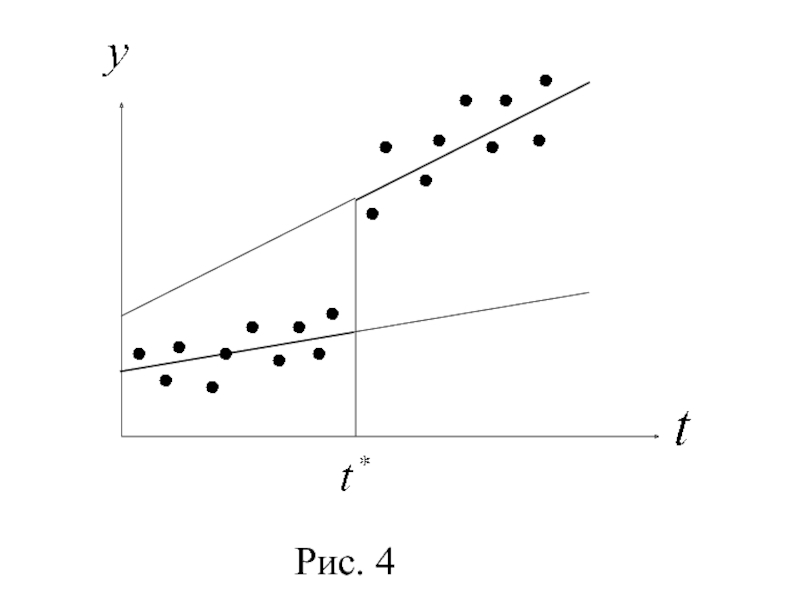
- 39. Рис. 4
- 40. 4°. Если оба параметра и
- 41. Выдвигается гипотеза о
- 42. больше , найденного
- 43. Таким образом,
Слайд 1Лекция 6
Модели с дискретными переменными
1. Фиктивные объясняющие переменные
2. Модели
3. Тесты Гуйарати и Чоу.
Слайд 21. Фиктивные объясняющие переменные
До сих пор рассматривались модели,
На практике возникает необходимость иссле-дования влияния на зависимую переменную каче-ственных признаков, которые могут принимать два или более фиксированных уровней, не явля-ющихся числовыми, а являющимися некоторыми категориями.
Слайд 3 Примерами таких признаков могут слу-жить: образование (начальное,
Чтобы учесть такие признаки в модели, они должны быть преобразованы в количе-ственные, т.е. им должны быть присвоены количественные метки. Сконструированные на основе качественных факторов числовые переменные называют фиктивными пере-менными (двоичными, индикаторными).
Слайд 4 Такие переменные приводят к скачкооб-разному изменению параметров
Регрессионные модели, содержащие лишь качественные факторы, называются ANOVA – моделями (моделями дисперси-онного анализа). Например, зависимость заработной платы от образования может быть представлена в виде:
Слайд 5где , если й
Нетрудно видеть, что ANOVA – моде-ли представляют собой кусочно-постоянные функции, и они достаточно редко использу-ются в экономике.
Чаще встречаются модели, содержащие как количественные, так и качественные факторы.
Слайд 6Такие модели называют ANCOVA-моделями (модели ковариационного анализа).
Обычно в
Слайд 7где , если служащий
Коэффициент в этой модели называют дифференциальным свободным членом, ибо он показывает, на какую величину изменится свободный член модели при изменении переменной .
Слайд 8 Если рассматриваемый качественный признак имеет более
В рассматриваемом примере о заработ-ной плате для учета влияния фактора образо-вания (начальное, среднее, высшее, т.е. ) на величину заработной платы необходимо ввести дополнительно в модель 2 бинарные переменные и :
Слайд 10Как видим, третьей фиктивной переменной не требуется, так как при
Нулевой уровень фиктивных перемен-ных называется базовым или сравнительным уровнем модели.
Оценку коэффициентов модели (1) в том числе и при фиктивных переменных выпол-няют МНК по той же схеме, как и при коли-чественных факторах модели, описанной выше.
Слайд 112. Модели с дискретными зависимыми переменными
Нередко зависимая
Изучим несколько типичных ситуаций и выделим основные виды таких переменных.
Слайд 12Номинальные переменные.
Рассмотрим следующие примеры.
1.
2. Решение о покупке товара: да, нет.
3. Выбор специальности при поступлении в институт: коммерсант, менеджер, экономист.
Слайд 13 Выбор значения осуществляется из двух или более
Если имеется только две возможности, то наблюдения обычно описываются бина-рной переменной.
В общем случае при наличии аль-тернатив результат можно описать перемен-ной, принимающей только целые значения: 1,2,3,…, .
Слайд 14 Главная особенность приведённых при-меров состоит в том,
Порядковые переменные.
Как и в предыдущем случае имеется несколько альтернатив, но они могут быть естественным образом упорядочены.
Слайд 151. Доход семьи: низкий, средний, высокий, очень высокий.
2. Уровень образования: начальное,
3. Состояние больного: плохое, удовлетвори-тельное, хорошее.
В качестве примеров рассмотрим:
Такие переменные называют порядковыми или ранговыми.
Слайд 16Количественные целочисленные переменные.
Примерами таких переменных служат:
2. Количество частных вузов в городе.
3. Число прибыльных фирм города
Слайд 17 Для моделей с описанными дискретными зависимыми переменными возможно
Однако с содержательной точки зрения удовлетворительные результаты можно по-лучить только для моделей с количествен-ными целочисленными переменными.
Слайд 18 Если зависимая переменная является номинальной
Поэтому стандартная схема оценки параметров модели в случае номинальных зависимых переменных нуждается в суще-ственной коррекции.
Слайд 19 Рассмотрим вначале простейшие модели бинарного выбора, когда
Изучим свойства таких моделей на при-мере покупки некоторой й семьёй авто-мобиля. Будем считать 1, если в течение исследуемого периода семья приобретёт автомобиль и 0 – в противном случае.
Слайд 20 На решение о покупке автомобиля влияют различные факторы:
На решение семьи влияют также неучтенные и случайные (расходы на лечение случайной болезни, расходы на ремонт квартиры после затопления соседями и т.д.) факторы .
Слайд 21 Выдвигая различные предположения о характере зависимости
Например, можно воспользоваться обы-чной линейной моделью регрессии:
Слайд 22 Поскольку , как случайная
то, находя математическое ожидание зависи-мой переменной, получим с учетом предпо-сылки 1°:
Слайд 23 В итоге модель (2) может быть записана в
и поэтому её называют линейной моделью вероятности.
Нетрудно показать, что модель (3) явля-ется гетероскедастичной. Другим важным недостатком модели является тот факт, что прогнозное значение зависимой переменной, вычисленное по полученному выборочному уравнению регрессии (правая часть уравне-ния (3))
Слайд 24
может находиться вне отрезка , что
Слайд 25 От указанного недостатка, связанного с предположением о
где некоторая функция с областью значений на отрезке .
Слайд 26 В частности, в качестве можно взять функцию
Наиболее распространенными функци-ями такого вида являются:
1. В качестве рассматривается функция стандартного нормального распределения вероятностей
и в этом случае модель (4) называют probit-моделью.
Слайд 272. Если в качестве выбирают логисти-ческую функцию
то говорят
Для оценивания коэффициентов probit- и logit-моделей обычно используют метод максимального правдоподобия.
Слайд 28 В том случае, когда номинальная зависимая переменная имеет
Допустим, что изучается выбор одной из трёх профессий: инженера, экономиста, юри-ста. Вводят в рассмотрение две бинарные переменные:
Слайд 29
Тогда выбор одного из трёх вариантов про-фессий можно описать
Слайд 313. Тесты Гуйарати и Чоу
Пусть требуется оценить парную регрессию, в которой
Предположим, что в момент времени произошло изменение характера динамики изучаемого показателя , вызванные струк-турными изменениями в экономике (эконо-мический кризис, природные катаклизмы и т.д.).
Слайд 32 Пусть до момента было произведено наблюдений
Тогда одной из задач анализа процесса является выяснения вопроса о том, значимо ли повлияли общие структурные изменения на параметры модели. Если это влияние зна-чимо, то для моделирования зависимости от времени следует использовать кусочно-линейные модели регрессии, т.е. одна модель будет описывать процесс до момента време-ни , а другая – после него.
Слайд 33 Если же структурные изменения незна-чительно повлияли на
Для ответа на этот вопрос в тесте Гуй-арати в модель регрессии включается фиктивная переменная :
Слайд 34где
В итоге для каждого промежутка времени получаются следующие оценки
для : ;
для : .
Слайд 35 С помощью критерия Стьюдента
Здесь возможны следующие случаи.
1°. Если статистически значим, а параметр нет, то изменение динамики вызвано различием свободных членов регрессии кусочно-линейной модели (рис. 2).
Слайд 382°. Если параметр статистически значим, а
3°. Если оба параметра и статистически значимы, то изменение зависимости приз-нака от времени вызвано как различием свободных членов, так и коэффициентов регрессии (рис. 4).
Слайд 404°. Если оба параметра и статистически незначимы,
Целесообразность применения двух уравне-ний регрессии вместо одного можно оценить, не прибегая к фиктивным переменным. Для этого используют тест Г. Чоу.
Слайд 41Выдвигается гипотеза о незначительном влиянии структурных изменений
Слайд 42больше , найденного по таблицам по заданному
В формуле (6) число пара-метров (без свободного члена) в уравнениях, построенных по статистическим данным до времени , после него и по всей совокуп-ности данных соответственно.
Слайд 43 Таким образом, в тесте Чоу в
по всей выборке (чтобы найти );
по выборке до времени (чтобы
определить );
по выборке после (чтобы вычислить