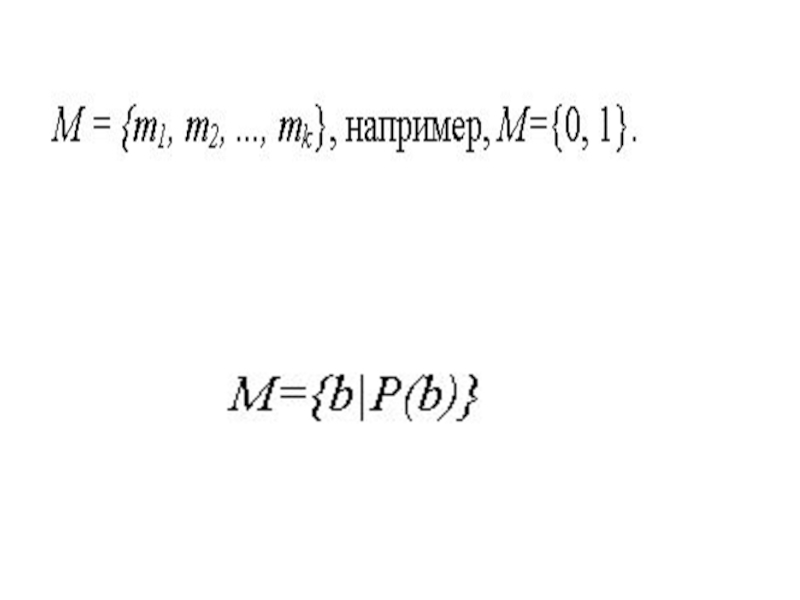- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы теории множеств презентация
Содержание
- 1. Основы теории множеств
- 2. Сегодня мы знаем, что, логически говоря,
- 3. Что такое множество? Совокупность элементов, объединенных некоторым
- 4. Принадлежность множеству
- 5. Способы задания множеств: Множество считается заданным, если
- 7. М составляют только те натуральные числа, что
- 8. Порождающая процедура - описывает способ получения элементов
- 9. Какое множество называется пустым? Существуют ли пустые
- 10. Как изображаются множества? а b M Диаграммы Эйлера-Венна
- 11. Что такое подмножество? Если каждый элемент
- 12. Подмножество K M
- 13. Универсальное множество Универсальным называют множество U, состоящее
- 14. Какие множества считаются равными? Равными называют два
- 15. Мощность множества Число элементов множества А называется мощностью множества и обозначается:
- 17. Операции над множествами.
- 18. Вопросы: Основные операции. Свойства операций над множествами. Декартово произведение множеств. *
- 19. Все правила достойного поведения давным-давно
- 20. 1. Основные операции. План изучения каждой
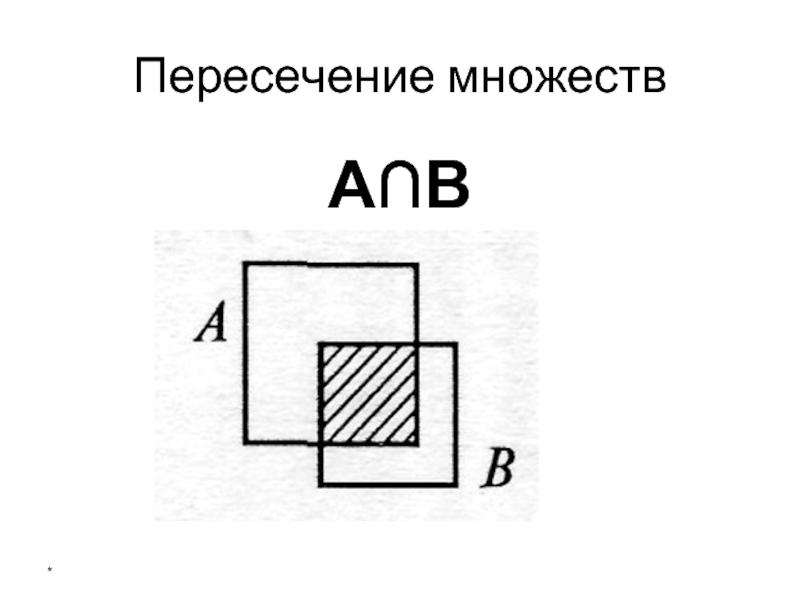
- 21. Пересечение множеств А∩В *
- 22. Пересечение множеств Те и только те элементы, которые принадлежат одновременно А и В *
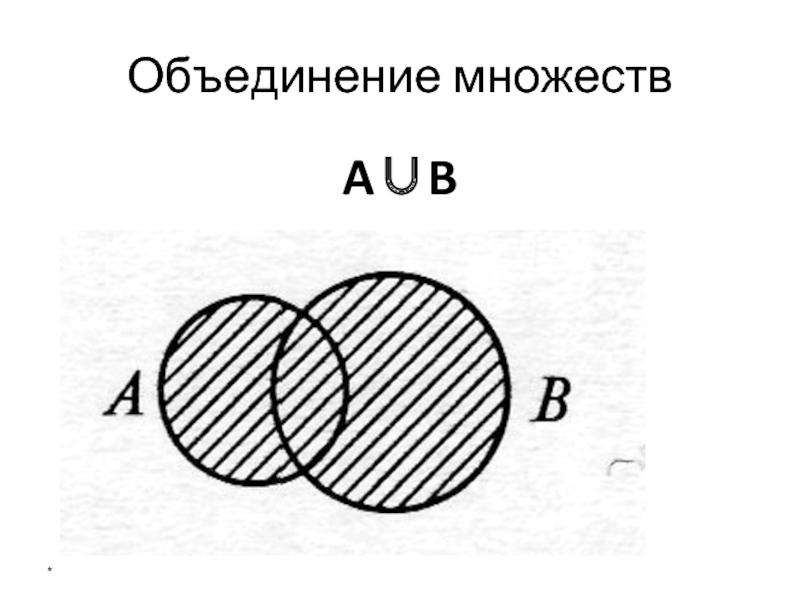
- 23. Объединение множеств A∪B *
- 24. Объединение множеств Те и только те элементы,
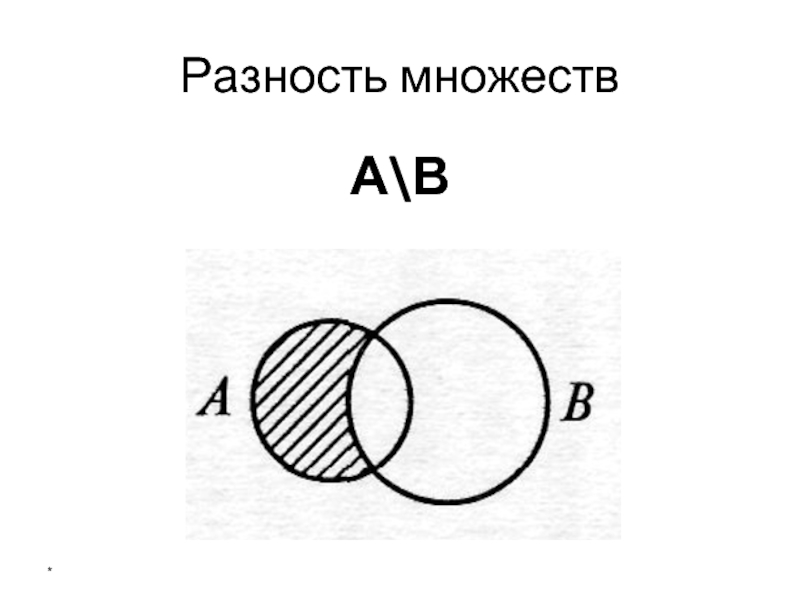
- 25. Разность множеств А\В *
- 26. Разность множеств Те и только те элементы множества А, которые не принадлежат В *
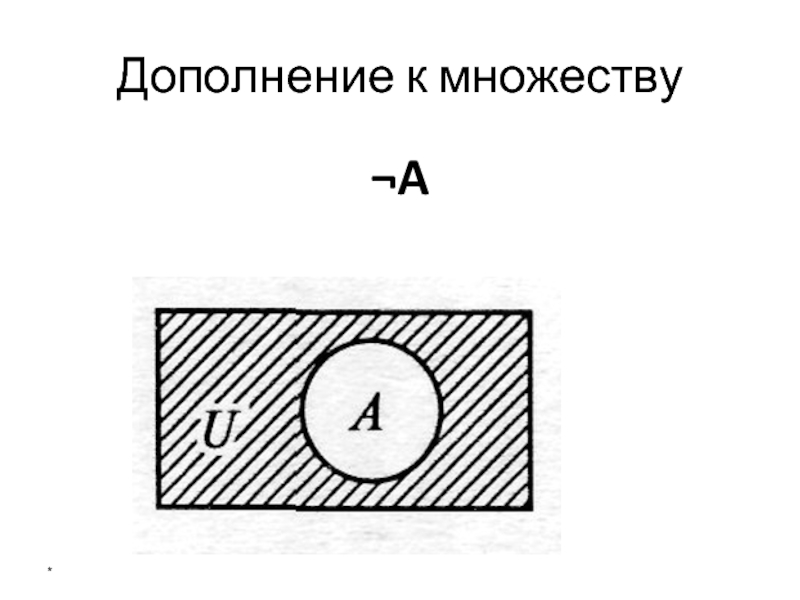
- 27. Дополнение к множеству ¬A *
- 28. Дополнение к множеству Те и только те элементы, которые не принадлежат множеству А *
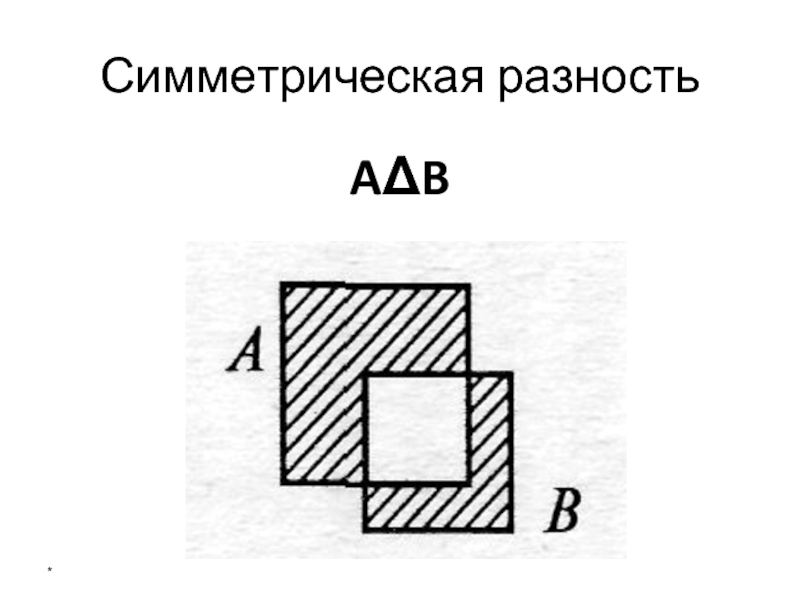
- 29. Симметрическая разность AΔB *
- 30. Симметрическая разность Те и только те элементы,
- 31. 2. Свойства операций над множествами. 1. A∪B
- 32. 2. Свойства операций над множествами. 7. A∪A=A
- 33. 2. Свойства операций над множествами. 14. A∩¬A
- 34. Разбиение множества Разбиение множества U - такая
- 35. 3. Декартово произведение множеств. Декартовым (прямым) произведением
- 36. 3. Декартово произведение множеств. 2) для n
- 37. 3. Декартово произведение множеств. если все Аi
- 38. Что вы сегодня узнали на уроке?
- 39. СПАСИБО ЗА ВНИМАНИЕ
Сегодня мы знаем, что, логически говоря, возможно вывести почти всю современную математику из единого источника — теории множеств. Н. Бурбаки
Слайд 2Сегодня мы знаем, что,
логически говоря,
возможно вывести почти всю современную
математику из единого источника —
теории множеств.
Н. Бурбаки
теории множеств.
Н. Бурбаки
Слайд 3Что такое множество?
Совокупность элементов, объединенных некоторым признаком, свойством, составляет понятие множество.
Предметы, составляющие множество, называются его элементами.
Слайд 5Способы задания множеств:
Множество считается заданным, если или перечислены все его элементы,
или указано свойство, которым обладают те и только те элементы, которые принадлежат данному множеству.
Слайд 7М составляют только те натуральные числа, что меньше пяти.
Само свойство
Р будем называть характеристическим.
Слайд 8Порождающая процедура - описывает способ получения элементов нового множества из уже
полученных элементов или из других объектов.
А = {Хк = 3 + 2(к2 +1)}, к = 0,1,2,...
Задавая различные значения параметра к, мы можем вычислять элементы множества А :
Х0 = 5, Х1 = 7, Х2 = 13 и т.д.
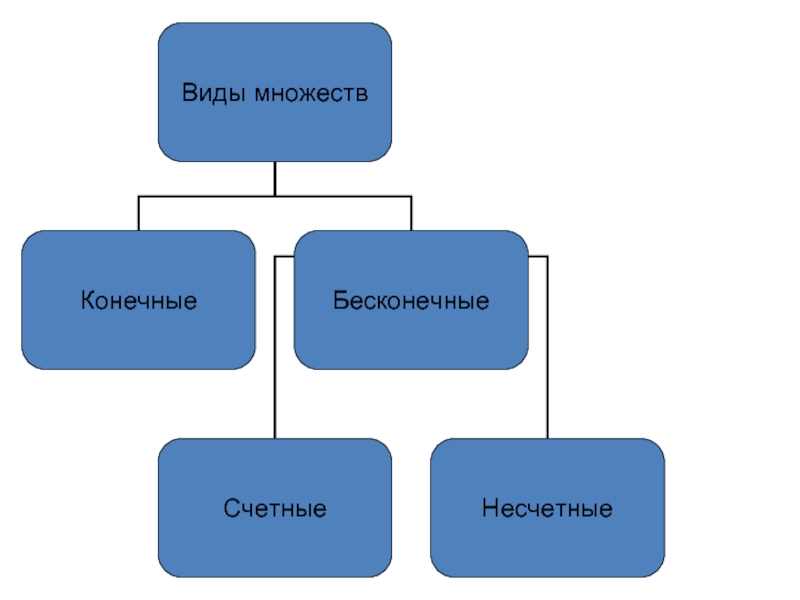
Слайд 9Какое множество называется пустым? Существуют ли пустые множества?
Множество, не содержащее
ни одного элемента, называется пустым и обозначается символом ∅.
Слайд 11Что такое подмножество?
Если каждый элемент множества А является в то
же время элементом множества В, то говорят, что А - подмножество в В, и пишут А⊂В.
Каждое непустое множество имеет по крайней мере два подмножества:
пустое множество ∅ и
само множество А.
Каждое непустое множество имеет по крайней мере два подмножества:
пустое множество ∅ и
само множество А.
Слайд 13Универсальное множество
Универсальным называют множество U, состоящее из всех возможных элементов, обладающих
данным признаком.
Например, множество планет Солнечной системы
U = {Земля, Марс, Венера, Юпитер, Сатурн, Уран, Плутон, Меркурий, Нептун}.
Например, множество планет Солнечной системы
U = {Земля, Марс, Венера, Юпитер, Сатурн, Уран, Плутон, Меркурий, Нептун}.
Слайд 14Какие множества считаются равными?
Равными называют два множества A и В, состоящие
из одинаковых элементов:
А=В
А=В
Слайд 15Мощность множества
Число элементов множества А называется мощностью множества и обозначается:
Слайд 18
Вопросы:
Основные операции.
Свойства операций над множествами.
Декартово произведение множеств.
*
Слайд 19Все правила
достойного поведения
давным-давно известны,
остановка за малым –
умением
ими пользоваться.
Б. Паскаль
Б. Паскаль
*
Слайд 201. Основные операции.
План изучения каждой операции:
Название
Обозначение
Изображение кругами Эйлера
Определение
Символическая запись
*
Слайд 24Объединение множеств
Те и только те элементы, которые принадлежат
хотя бы одному
из множеств А и В
*
Слайд 30Симметрическая разность
Те и только те элементы, которые принадлежат одному из множеств:
А либо В, но не являются их общими элементами
*
Слайд 312. Свойства операций над множествами.
1. A∪B = B∪A коммутативность
2. А∩В =
В∩А коммутативность
3. (А∪В) ∪С = А∪ (В∪С) ассоциативность
4.(А∩В) ∩С = А∩ (В∩С) ассоциативность
5. (А∪В) ∩С = (А∩С) ∪ (В∩С)
дистрибутивность
6. (А∩В) ∪С = (А∪С) ∩ (В∪С) дистрибутивность
3. (А∪В) ∪С = А∪ (В∪С) ассоциативность
4.(А∩В) ∩С = А∩ (В∩С) ассоциативность
5. (А∪В) ∩С = (А∩С) ∪ (В∩С)
дистрибутивность
6. (А∩В) ∪С = (А∪С) ∩ (В∪С) дистрибутивность
*
Слайд 322. Свойства операций над множествами.
7. A∪A=A
8. А∩А = А
9. A∪(A∩B) =
A закон поглощения
10. A∩ (A∪B) = A закон поглощения
11. ¬(A∪B) =¬ A∩¬B закон де Моргана
12. ¬(A∩B) =¬ A∪¬B закон де Моргана
13. A∪¬A=U
10. A∩ (A∪B) = A закон поглощения
11. ¬(A∪B) =¬ A∩¬B закон де Моргана
12. ¬(A∩B) =¬ A∪¬B закон де Моргана
13. A∪¬A=U
*
Слайд 332. Свойства операций над множествами.
14. A∩¬A = ∅
15. A∪∅ = A
16.
А∩∅ = ∅
17. A∪U = U
18. A∩U = A
19. ¬U= ∅
20. ¬∅=U
21. ¬(¬A)=A закон двойного отрицания
17. A∪U = U
18. A∩U = A
19. ¬U= ∅
20. ¬∅=U
21. ¬(¬A)=A закон двойного отрицания
*
Слайд 34Разбиение множества
Разбиение множества U - такая система непустых подмножеств {Аа}
множества
U ,что
их объединение равно U (полнота разбиения),
а все попарные пересечения - пусты (чистота разбиения).
Сами Аа называются классами, или блоками, разбиения.
их объединение равно U (полнота разбиения),
а все попарные пересечения - пусты (чистота разбиения).
Сами Аа называются классами, или блоками, разбиения.
*
Слайд 353. Декартово произведение множеств.
Декартовым (прямым) произведением множеств называется
1) для двух множеств
А, В: произведение А× В - множество всех пар (а,b), где а∈A,b∈В;
*
Слайд 363. Декартово произведение множеств.
2) для n множеств А1,А2,...,Аn:
произведение А1×А2×...×Аn -множество
всех векторов (a1,a2,...,an), где ai ∈ Аi
(т.е. a1∈ А1 ,а2∈ А2, ..., аn∈ Аn);
(т.е. a1∈ А1 ,а2∈ А2, ..., аn∈ Аn);
*
Слайд 373. Декартово произведение множеств.
если все Аi одинаковы и равны A, то
произведение A×A×…×A обозначается Аn и называется n-й степенью множества А.
A×A×…×A= Аn
A×A×…×A= Аn
*
