митної справи та фінансів
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ВМП. Математичне програмування та дослідження операцій. Метод штучного базису М-метод. (Лекція 3) презентация
Содержание
- 1. ВМП. Математичне програмування та дослідження операцій. Метод штучного базису М-метод. (Лекція 3)
- 2. Тема 7: Метод штучного базису М-метод
- 3. Умова застосування М-методу Під час розв’язування задачі
- 4. Ідея застосування М-методу Ідея полягає в тому,
- 5. Правила введення штучних змінних У цільовій
- 6. Алгоритм М-методу Значення оцінок опорного плану в
- 7. Алгоритм М-методу
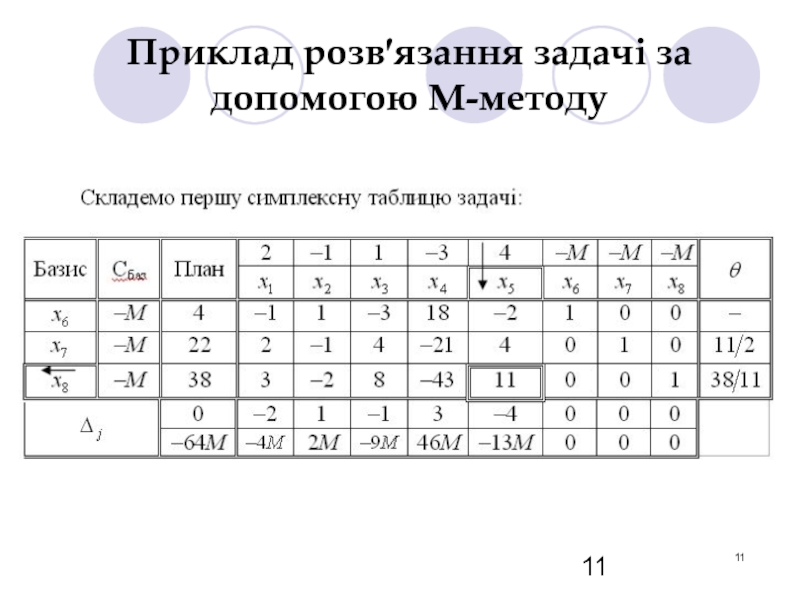
- 8. Приклад розв′язання задачі за допомогою М-методу
- 9. Приклад розв′язання задачі за допомогою М-методу
- 10. Приклад розв′язання задачі за допомогою М-методу
- 11. Приклад розв′язання задачі за допомогою М-методу
- 12. Приклад розв′язання задачі за допомогою М-методу
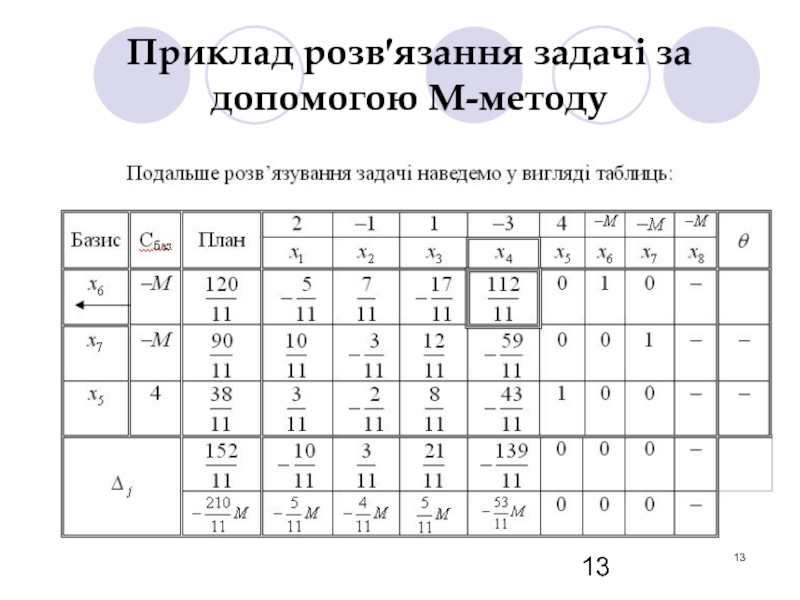
- 13. Приклад розв′язання задачі за допомогою М-методу
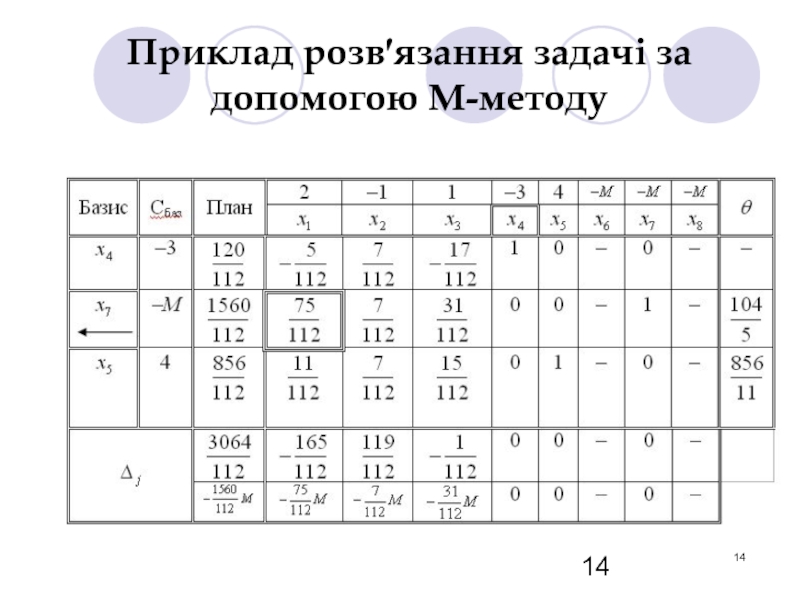
- 14. Приклад розв′язання задачі за допомогою М-методу
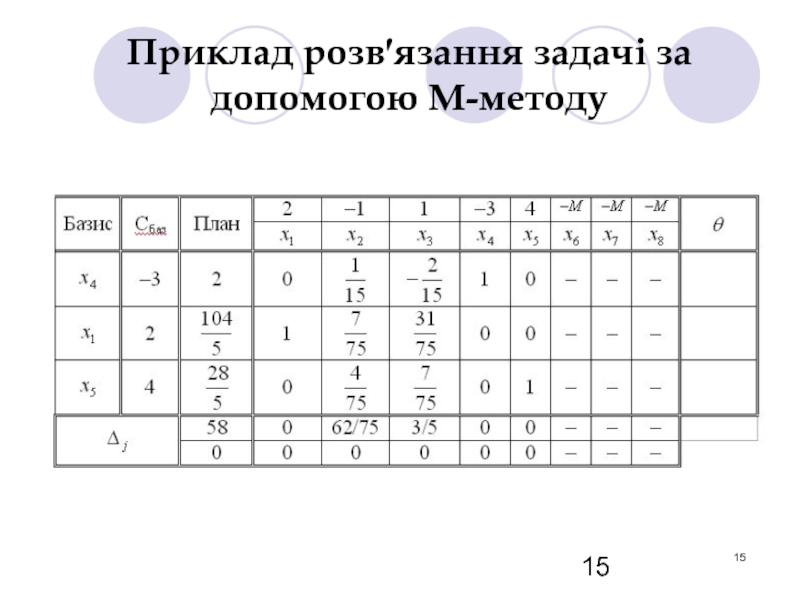
- 15. Приклад розв′язання задачі за допомогою М-методу
- 16. Приклад розв′язання задачі за допомогою М-методу
- 17. Тема 8: Методика розв'язування транспортних задач
- 18. Постановка транспортної задачі Транспортні
- 19. Постановка транспортної задачі
- 20. Постановка транспортної задачі
- 21. Математична постановка транспортної задачі
- 22. Основні поняття транспортної задачі
- 23. Умова існування розв'язку транспортної задачі
- 24. Алгоритм розв'язання транспортної задачі Визначення типу транспортної
- 25. Алгоритм розв'язання транспортної задачі (визначення типу задачі)
- 26. Методи пошуку початкового опорного плану
- 27. Метод північно-західного кута пошуку початкового опорного плану
- 28. Перевірка початкового опорного плану
- 29. Метод мінімальної вартості пошуку початкового опорного плану
- 30. Метод Фогеля пошуку початкового опорного плану На
- 31. Метод потенціалів пошуку оптимального плану
- 32. Метод потенціалів пошуку оптимального плану
- 33. Метод потенціалів пошуку оптимального плану
- 34. Метод потенціалів пошуку оптимального плану
- 35. Правила побудови циклу перерозподілу вантажу
- 36. Тема 9: Задачі цілочислового лінійного програмування
- 37. Задачі цілочислового лінійного програмування
- 38. Постановка задачі цілочислового лінійного програмування
- 39. Методи розв’язування задач ціло-числового лінійного програмування
- 40. Ідея методів відтинань
- 41. Ідея комбінаторних методів
- 42. Ідея задачі на призначення
- 43. Математична постановка задачі на призначення
- 44. Задача на призначення
- 45. Алгоритм угорського методу розв’язання задачі на призначення
- 46. Алгоритм угорського методу розв’язання задачі на призначення
- 47. Алгоритм угорського методу розв’язання задачі на призначення
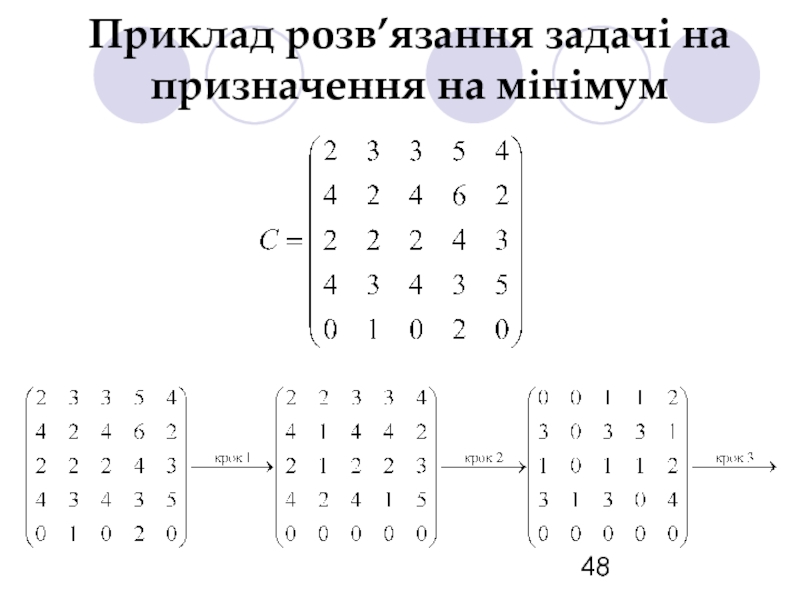
- 48. Приклад розв’язання задачі на призначення на мінімум
- 49. Приклад розв’язання задачі на призначення на мінімум
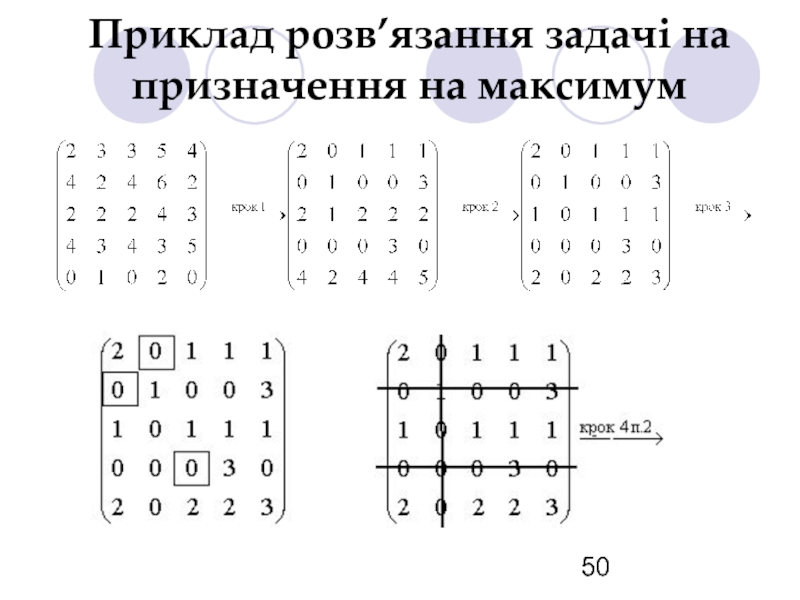
- 50. Приклад розв’язання задачі на призначення на максимум
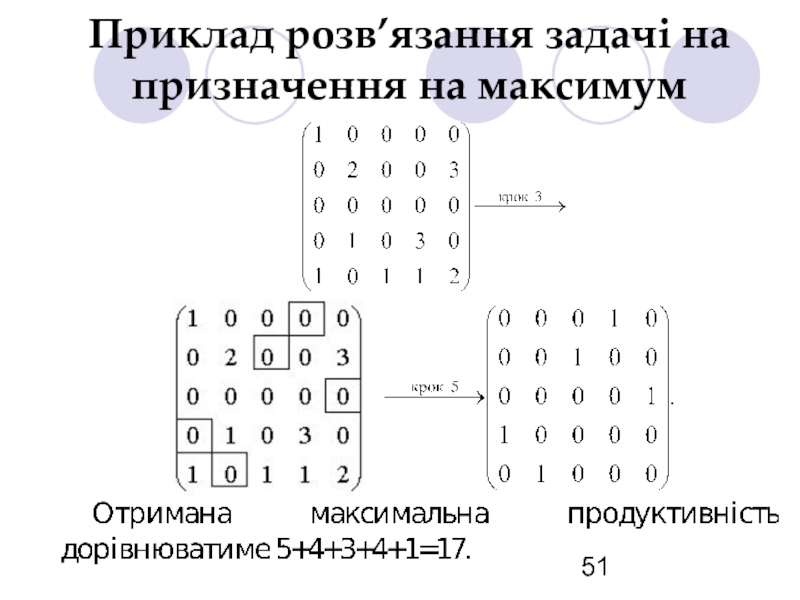
- 51. Приклад розв’язання задачі на призначення на максимум
- 52. Метод Гоморі розв’язування задач цілочислового лінійного програмування
- 53. Метод Гоморі розв’язування задач цілочислового лінійного програмування
- 54. Метод Гоморі розв’язування задач цілочислового лінійного програмування
- 55. Геометрична інтерпретація методу Гоморі
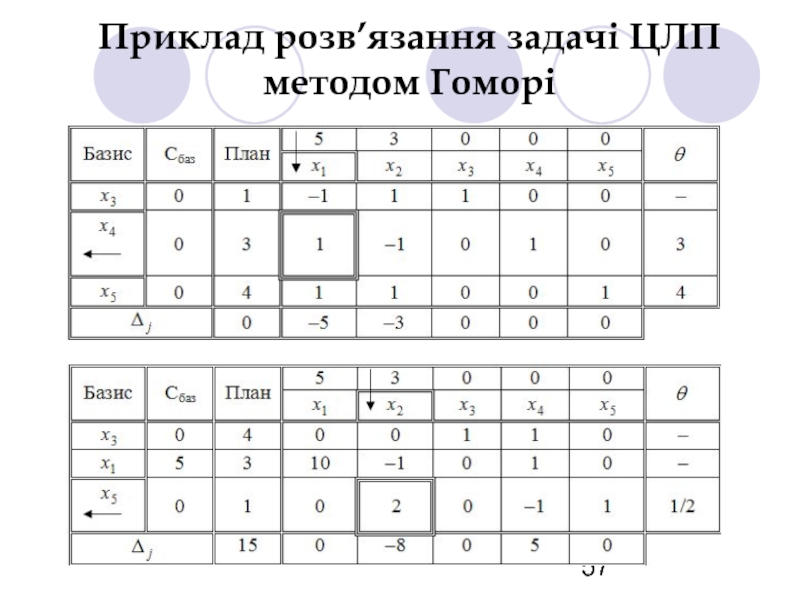
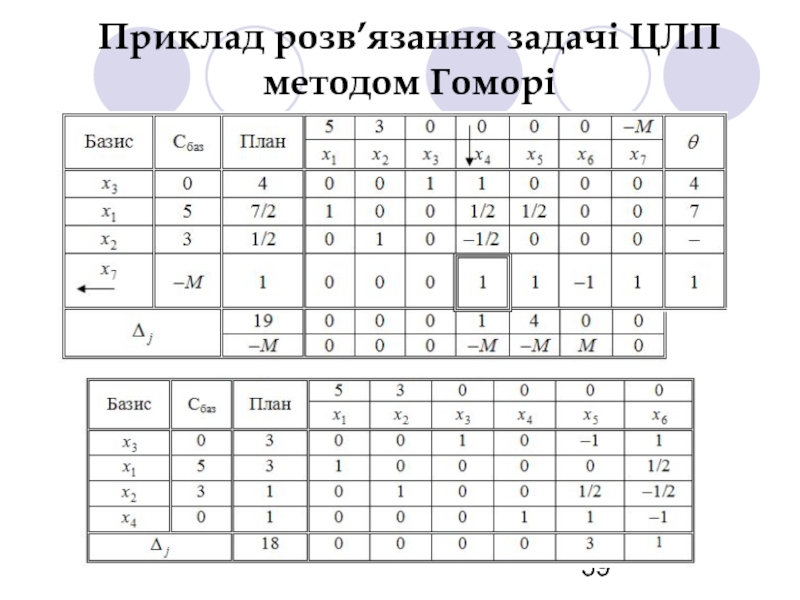
- 56. Приклад розв’язання задачі ЦЛП методом Гоморі
- 57. Приклад розв’язання задачі ЦЛП методом Гоморі
- 58. Приклад розв’язання задачі ЦЛП методом Гоморі
- 59. Приклад розв’язання задачі ЦЛП методом Гоморі
- 60. Схема методу гілок та меж
- 61. Схема методу гілок та меж
- 62. Схема методу гілок та меж
- 63. Розгалуження методу гілок та меж
- 64. Схема методу гілок та меж
- 65. Геометрична інтерпретація розгалуження
- 66. Геометрична інтерпретація розгалуження
- 67. Алгоритм методу гілок та меж
- 68. Алгоритм методу гілок та меж
- 69. Алгоритм методу гілок та меж
- 70. Графічний метод гілок та меж
- 71. Результати застосування графічного методу гілок та меж
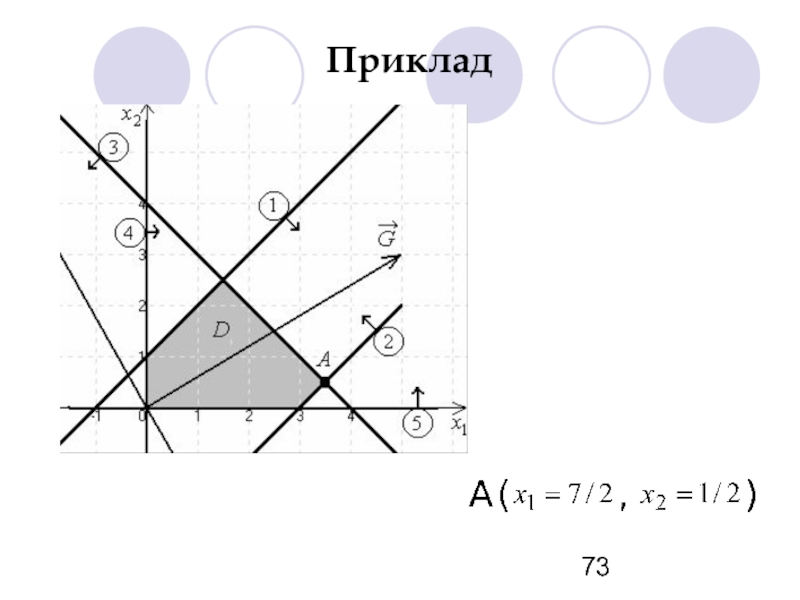
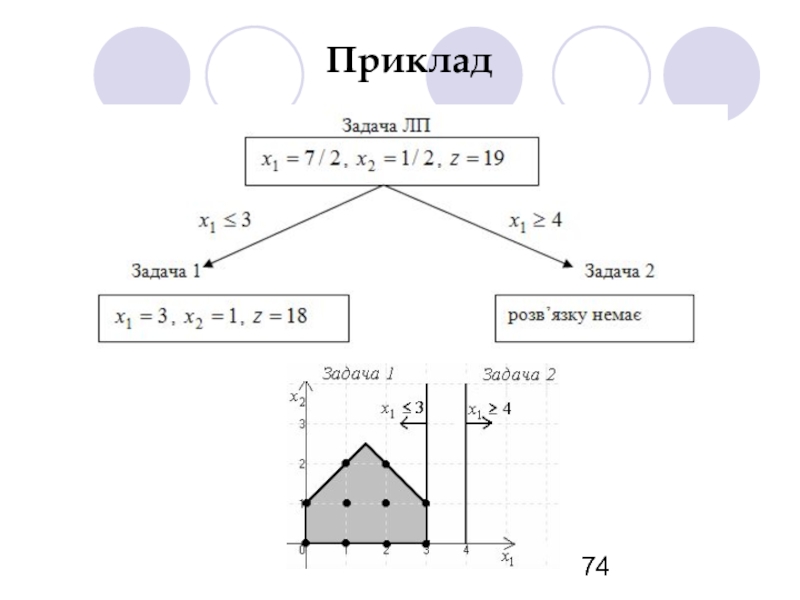
- 72. Приклад
- 73. Приклад
- 74. Приклад
- 75. Приклад
- 76. Список літератури Основна: Зайченко Ю. П. Дослідження
Слайд 1Вища та прикладна математика
Модуль: Математичне програмування та дослідження операцій
доц. Лебідь О.Ю.
Дніпропетровськ
2016
Університет
Слайд 2Тема 7: Метод штучного базису
М-метод
План
Умова застосування М-методу
Правила
введення штучних змінних.
Алгоритм М-методу.
Приклад.
Алгоритм М-методу.
Приклад.
Слайд 3Умова застосування М-методу
Під час розв’язування задачі лінійної оптимізації симплекс-методом можлива ситуація,
коли при визначенні початкового опорного плану в системі обмежень немає необхідної кількості одиничних лінійно-незалежних векторів.
Для побудови початкового плану застосовують метод штучного базису.
Для побудови початкового плану застосовують метод штучного базису.
Слайд 4Ідея застосування М-методу
Ідея полягає в тому, що відсутні одиничні вектори можна
дістати, увівши до відповідних обмежень деякі змінні з коефіцієнтом +1, що називаються штучними.
Слайд 5Правила введення штучних
змінних
У цільовій функції задачі лінійної оптимізації штучні змінні
мають коефіцієнт
–М (для задачі на максимум),
де М – досить велике додатне число.
–М (для задачі на максимум),
де М – досить велике додатне число.
Слайд 6Алгоритм М-методу
Значення оцінок опорного плану в симплексній таблиці складаються з двох
частин: одна містить М, а інша – просто число. Тому розбиваємо рядок оцінок у таблиці на два: у перший записуємо просто число, а в другий – коефіцієнт при М.
Якщо опорний план не є оптимальним, тоді при визначенні змінної, яка буде вводитись до базису, спочатку дивимось на другий рядок оцінок. Коли в ньому всі оцінки відповідають умові оптимальності, тоді переглядаємо перший рядок оцінок.
Якщо опорний план не є оптимальним, тоді при визначенні змінної, яка буде вводитись до базису, спочатку дивимось на другий рядок оцінок. Коли в ньому всі оцінки відповідають умові оптимальності, тоді переглядаємо перший рядок оцінок.
Слайд 17Тема 8: Методика розв'язування транспортних задач
План
Постановка транспортної задачі
Умова існування розв'язку транспор-тної задачі
Алгоритм розв'язування транспортної задачі за загальним критерієм вартості
Методи пошуку опорного початкового плану
Метод потенціалів для розв'язування транспортної задачі
Алгоритм розв'язування транспортної задачі за загальним критерієм вартості
Методи пошуку опорного початкового плану
Метод потенціалів для розв'язування транспортної задачі
Слайд 18Постановка транспортної задачі
Транспортні задачі – спеціальний клас задач
лінійної оптимізації. Ці задачі найчастіше описують перевезення деякого товару з пункту відправлення (постачальників) до пункту призначення (споживачів).
Призначення транспортної задачі – визначення об’єму перевезень з пунктів відправлення до пунктів призначення з мінімальною вартістю перевезень. При цьому повинні враховуватися обмеження, які накладені на об’єм вантажу, який є у пунктах відправлення (пропозиція), та обмеження, які враховують необхідність вантажу в пунктах призначення (попит).
Призначення транспортної задачі – визначення об’єму перевезень з пунктів відправлення до пунктів призначення з мінімальною вартістю перевезень. При цьому повинні враховуватися обмеження, які накладені на об’єм вантажу, який є у пунктах відправлення (пропозиція), та обмеження, які враховують необхідність вантажу в пунктах призначення (попит).
Слайд 24Алгоритм розв'язання транспортної задачі
Визначення типу транспортної задачі (відкрита чи закрита).
Побудова початкового
опорного плану транспортної задачі.
Перевірка плану транспортної задачі на оптимальність.
Якщо умова оптимальності виконується, то маємо оптимальний розв’язок транспортної задачі. Якщо ж умова оптимальності не виконується, необхідно перейти до наступного опорного плану та перейти на пункт 3.
Перевірка плану транспортної задачі на оптимальність.
Якщо умова оптимальності виконується, то маємо оптимальний розв’язок транспортної задачі. Якщо ж умова оптимальності не виконується, необхідно перейти до наступного опорного плану та перейти на пункт 3.
Слайд 29Метод мінімальної вартості пошуку початкового опорного плану
Ідея методу мінімальної вартості полягає
в тому, що на кожному кроці заповнюють клітинку таблиці, яка має найменшу вартість перевезення одиниці продукції.
Такі дії повторюють доти, доки не буде розподілено всю продукцію між постачальниками та споживачами.
Такі дії повторюють доти, доки не буде розподілено всю продукцію між постачальниками та споживачами.
Слайд 30Метод Фогеля пошуку початкового опорного плану
На кожному кроці визначають різницю між
двома найменшими вартостями в кожному рядку і стовпці транспортної таблиці.
Ці різниці записують у спеціально відведених місцях таблиці.
Серед усіх різниць вибирають найбільшу і у відповідному рядку чи стовпці заповнюють клітинку з найменшою вартістю.
Якщо ж однакових найбільших різниць кілька, то вибирають будь-який відповідний рядок або стовпець.
Коли залишається незаповненим лише один рядок або стовпець, то обчислення різниць припиняють, а таблицю продовжують заповнювати за методом мінімальної вартості.
Ці різниці записують у спеціально відведених місцях таблиці.
Серед усіх різниць вибирають найбільшу і у відповідному рядку чи стовпці заповнюють клітинку з найменшою вартістю.
Якщо ж однакових найбільших різниць кілька, то вибирають будь-який відповідний рядок або стовпець.
Коли залишається незаповненим лише один рядок або стовпець, то обчислення різниць припиняють, а таблицю продовжують заповнювати за методом мінімальної вартості.
Слайд 36Тема 9: Задачі цілочислового лінійного програмування
План
Постановка задачі цілочислового лінійного
програмування (ЦЛП)
Методи розв'язування задач ЦЛП
Задача на призначення
Алгоритм угорського методу розв'язання задачі на призначення
Метод Гоморі розв'язування задач ЦЛП
Метод гілок та меж розв'язування задач ЦЛП
Методи розв'язування задач ЦЛП
Задача на призначення
Алгоритм угорського методу розв'язання задачі на призначення
Метод Гоморі розв'язування задач ЦЛП
Метод гілок та меж розв'язування задач ЦЛП
Слайд 76Список літератури
Основна:
Зайченко Ю. П. Дослідження операцій : підручник / Ю. П. Зайченко. –
К. : ВІПОЛ, 2000.
Таха Х. Введение в исследование операций / Х. Таха. – М. : Вильямс, 2001.
Ульянченко О. В. Дослідження операцій в економіці / О. В. Ульянченко. – Х. : Гриф, 2003.
Додаткова:
Вітлінський В. В. Математичне програмування / В. В. Вітлінський, С. І. Наконечний, Т. О. Терещенко. – К., 2001.
Кузнецов А. В. Математическое программирование / А. В. Кузнецов и др. – М.: Высшая школа, 1994.
Таха Х. Введение в исследование операций / Х. Таха. – М. : Вильямс, 2001.
Ульянченко О. В. Дослідження операцій в економіці / О. В. Ульянченко. – Х. : Гриф, 2003.
Додаткова:
Вітлінський В. В. Математичне програмування / В. В. Вітлінський, С. І. Наконечний, Т. О. Терещенко. – К., 2001.
Кузнецов А. В. Математическое программирование / А. В. Кузнецов и др. – М.: Высшая школа, 1994.