критического?
Какие виды отказов подразумевают значительный ущерб для окружающей среды?
Насколько глубоко следует анализировать редкий некритический отказ?
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вероятность. Вычисление вероятности презентация
Содержание
- 1. Вероятность. Вычисление вероятности
- 2. Вопросы по предыдущей лекции Что такое множество?
- 3. Вопросы по предыдущей лекции Множество В является
- 4. Вопросы по предыдущей лекции Что такое объединение
- 5. Вопросы по предыдущей лекции Что такое событие?
- 6. 2.3. Вероятность Вероятность – численная мера
- 7. Аксиомы вероятности 1. Р(А) – число от
- 8. Как вычислить вероятность? Есть 2 подхода:
- 9. 1. Априорное (классическое) определение вероятности Если результат
- 10. 2. Апостериорное (статистическое) определение вероятности Вероятность события
- 11. Условная вероятность Пусть вероятность события А зависит
- 12. Независимые события События называются независимыми, если наступление
- 13. Умножение вероятностей а) Независимые события Р(АВ) =
- 14. Сложение вероятностей а) Совместные и независимые события
- 15. Сложение вероятностей б) Совместные и зависимые события
- 16. Сложение вероятностей в) Несовместные события Р(А
- 17. Сложение вероятностей г) Противоположные события Р(А) +
- 18. Формула полной вероятности Пусть Н1, Н2, …
- 19. К формуле полной вероятности Н1 Н2 Н3 Н4
- 20. К формуле полной вероятности А
- 21. К формуле полной вероятности А Н1 Н2 Н3 Н4
- 22. К формуле полной вероятности А Н2
- 23. Формула Байеса Пусть Н1, Н2, … ,
- 24. В формуле Байеса: Дано: Р(Нi) –
- 25. Пример применения формулы Байеса По линии связи
- 26. Решение Рассматриваем гипотезы: Н1 – посылается сигнал
Слайд 1Вопросы по предыдущей лекции
Что такое критический отказ?
Чем некритический отказ отличается от
Слайд 2Вопросы по предыдущей лекции
Что такое множество?
Чем определяются соотношения между множествами?
Зачем нужны
диаграммы Эйлера-Венна?
Приведите определение и пример пересекающихся множеств.
Приведите определение и пример ситуации, когда множество В является подмножеством А.
Приведите определение и пример пересекающихся множеств.
Приведите определение и пример ситуации, когда множество В является подмножеством А.
Слайд 3Вопросы по предыдущей лекции
Множество В является подмножеством А. Чему равно их
пересечение? объединение?
Перечислите операции над множествами.
Перечислите операции над множествами.
Слайд 4Вопросы по предыдущей лекции
Что такое объединение множеств?
Что такое пересечение множеств?
Что такое
разность множеств?
Что такое дополнение множества?
Что такое дополнение множества?
Слайд 5Вопросы по предыдущей лекции
Что такое событие?
Что называется достоверным событием?
Что такое случайное
событие?
Что такое совместные события?
Что такое несовместные события?
Какие события называются противоположными?
Что такое полная группа событий?
Что такое группа гипотез?
В каком случае гипотезы называются равно-возможными?
Что такое совместные события?
Что такое несовместные события?
Какие события называются противоположными?
Что такое полная группа событий?
Что такое группа гипотез?
В каком случае гипотезы называются равно-возможными?
Слайд 62.3. Вероятность
Вероятность –
численная мера
степени объективной возможности
наступления случайного события.
Обозначение:
Р(А)
06.10.17
Занятие 3
Слайд 7Аксиомы вероятности
1. Р(А) – число от 0 до 1
2. Р(S) =
1; P(U) = 1; P(V) = 0
3. Если А и В несовместны, то Р(А + В) = Р(А) + Р(В)
На основе этих аксиом строится вся теория вероятности.
Из аксиомы 3 следует: Р(А) = 1 – Р(А)
3. Если А и В несовместны, то Р(А + В) = Р(А) + Р(В)
На основе этих аксиом строится вся теория вероятности.
Из аксиомы 3 следует: Р(А) = 1 – Р(А)
Слайд 8Как вычислить вероятность?
Есть 2 подхода:
1. На основе рассуждений
(априорные вероятности, то
есть
«до опыта»).
2. На основе опыта (апостериорные вероятности, то есть «после опыта»).
2. На основе опыта (апостериорные вероятности, то есть «после опыта»).
Слайд 91. Априорное (классическое) определение вероятности
Если результат опыта можно представить в виде
группы равновозможных гипотез (исходов), то вероятность события А равна:
Р(А) = m/n,
где m – число исходов, благоприятствующих событию А;
n – общее число всех возможных исходов.
Р(А) = m/n,
где m – число исходов, благоприятствующих событию А;
n – общее число всех возможных исходов.
Слайд 102. Апостериорное (статистическое) определение вероятности
Вероятность события А равна:
Р(А) = lim
m/n
n → ∞
где m – количество появлений события А;
n – количество испытаний при достаточно большом их числе
n → ∞
где m – количество появлений события А;
n – количество испытаний при достаточно большом их числе
Слайд 11Условная вероятность
Пусть вероятность события А зависит от того, произошло или не
произошло событие В.
Такие события называются зависимыми.
Такая вероятность называется условной:
Р(А|В) - вероятность А при условии В
или
РВ(А)
Формула для вычисления условной вероятности:
Р(А|В) = Р(АВ) / Р(В)
Такие события называются зависимыми.
Такая вероятность называется условной:
Р(А|В) - вероятность А при условии В
или
РВ(А)
Формула для вычисления условной вероятности:
Р(А|В) = Р(АВ) / Р(В)
Слайд 12Независимые события
События называются независимыми, если наступление одного из них не изменяет
вероятности второго.
То есть, когда:
Р(А|В) = Р(А)
То есть, когда:
Р(А|В) = Р(А)
Слайд 13Умножение вероятностей
а) Независимые события
Р(АВ) = Р(А) ∙ Р(В)
Р(А1А2…Аn) = Р(А1) ∙
Р(А2) ∙ … ∙ Р(Аn)
б) Зависимые события
Р(АВ) = Р(А) ∙ Р(B|A)
Р(А1А2…Аn) = Р(А1) ∙ Р(А2|A1) ∙ Р(А3|A1A2) ∙ …
б) Зависимые события
Р(АВ) = Р(А) ∙ Р(B|A)
Р(А1А2…Аn) = Р(А1) ∙ Р(А2|A1) ∙ Р(А3|A1A2) ∙ …
Слайд 14Сложение вероятностей
а) Совместные и независимые события
Р(А + В) = Р(А) +
Р(В) – Р(АВ)
Р(А + В + С) =
= Р(А) + Р(В) + Р(С) – Р(АВ) – Р(ВС) – Р(АС) + Р(АВС)
Р(А + В + С + D) =
= Р(А) + Р(В) + Р(С) + Р(D) – – Р(АВ) – Р(AС) – Р(AD) – Р(BC) – Р(BD) – Р(СD) + + Р(АВС) + Р(АВD) + Р(AСD) + Р(ВСD) – P(ABCD)
Р(А + В + С) =
= Р(А) + Р(В) + Р(С) – Р(АВ) – Р(ВС) – Р(АС) + Р(АВС)
Р(А + В + С + D) =
= Р(А) + Р(В) + Р(С) + Р(D) – – Р(АВ) – Р(AС) – Р(AD) – Р(BC) – Р(BD) – Р(СD) + + Р(АВС) + Р(АВD) + Р(AСD) + Р(ВСD) – P(ABCD)
Слайд 15Сложение вероятностей
б) Совместные и зависимые события
Р(А + В) = Р(А) +
Р(В) – Р(А) ∙ Р(В|А)
Слайд 16Сложение вероятностей
в) Несовместные события
Р(А + В) = Р(А) + Р(В)
Р(А1 +
А2 + … + Аn) = Р(А1) + Р(А2) + … + Р(Аn)
Слайд 17Сложение вероятностей
г) Противоположные события
Р(А) + Р(А) = 1
д) Группа гипотез
Р(Н1) +
Р(Н2) + … + Р(Нn) = 1
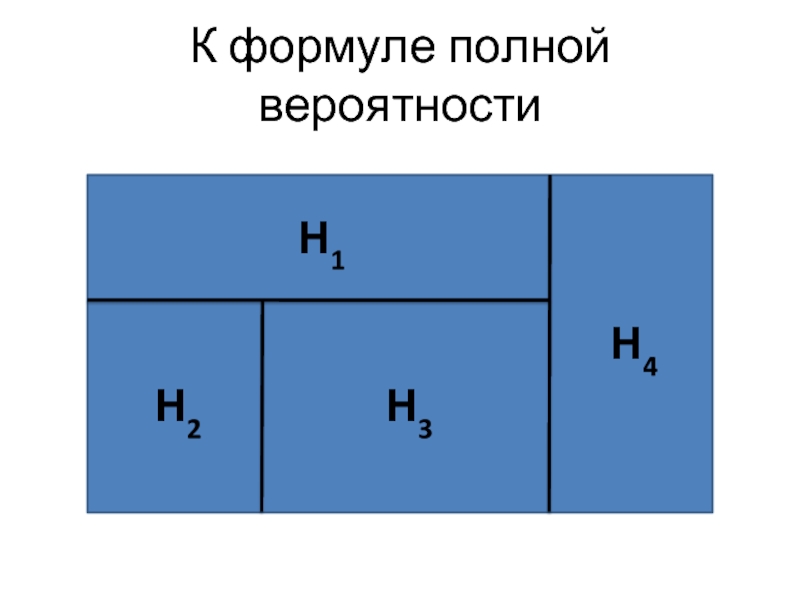
Слайд 18Формула полной вероятности
Пусть Н1, Н2, … , Нn – группа гипотез.
Пусть
событие А может наступить лишь при условии появления одной из гипотез.
Тогда вероятность события А равна:
Р(А) = Р(Н1)∙Р(А|Н1) + Р(Н2)∙Р(А|Н2) +…+Р(Нn)∙Р(А|Нn)
Тогда вероятность события А равна:
Р(А) = Р(Н1)∙Р(А|Н1) + Р(Н2)∙Р(А|Н2) +…+Р(Нn)∙Р(А|Нn)
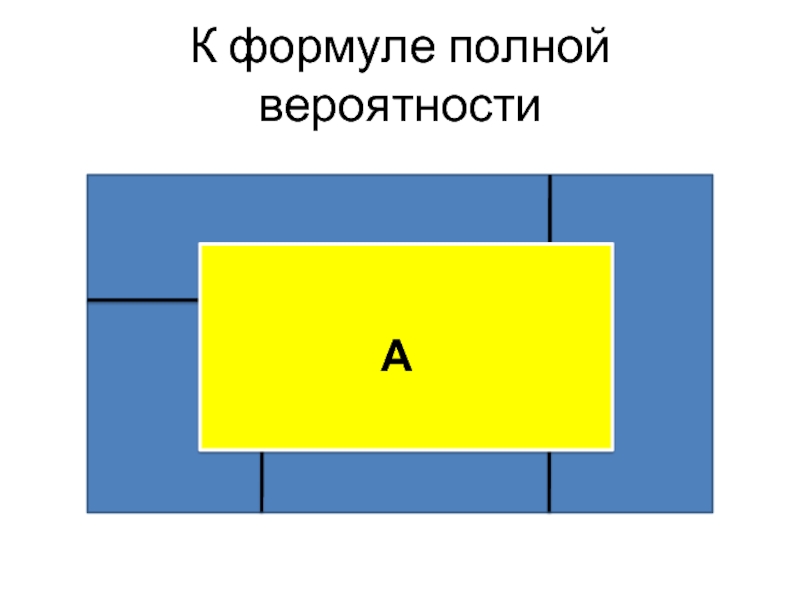
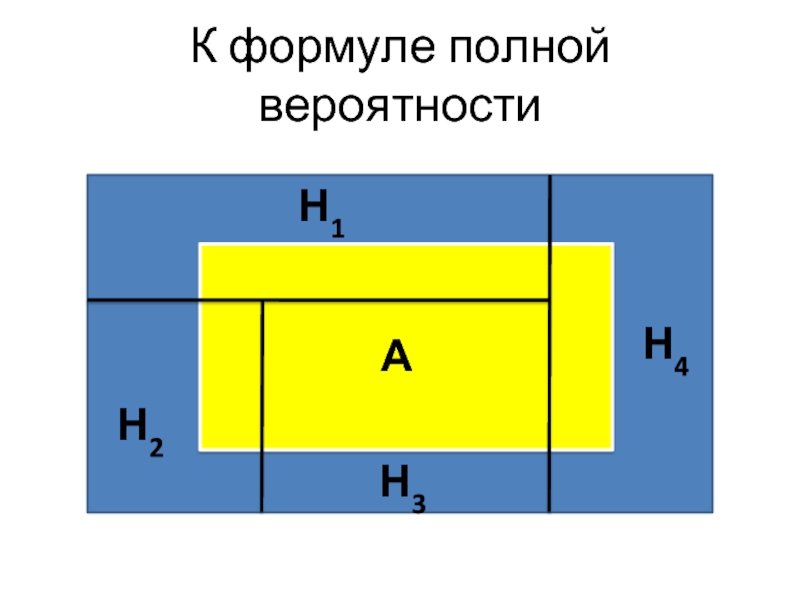
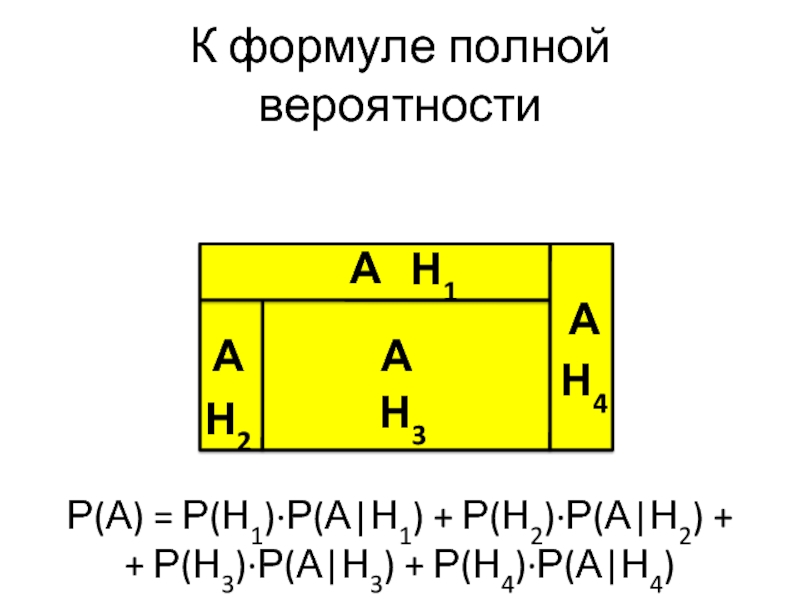
Слайд 22К формуле полной вероятности
А
Н2
Н3
Н4
А
А
Н1
А
Р(А) = Р(Н1)∙Р(А|Н1) + Р(Н2)∙Р(А|Н2) +
+ Р(Н3)∙Р(А|Н3)
+ Р(Н4)∙Р(А|Н4)
Слайд 23Формула Байеса
Пусть Н1, Н2, … , Нn – группа гипотез.
Пусть событие
А может наступить лишь при условии появления одной из гипотез.
Проведён опыт, в результате которого появилось событие А.
Тогда вероятность того, что событие А произошло в результате определённой гипотезы Нi , равна:
Проведён опыт, в результате которого появилось событие А.
Тогда вероятность того, что событие А произошло в результате определённой гипотезы Нi , равна:
Слайд 24В формуле Байеса:
Дано:
Р(Нi) – априорная вероятность гипотезы Нi (насколько вероятна причина
вообще Нi, то есть до опыта);
Р(A|Нi) – вероятность события А при истинности гипотезы Нi.
Найти:
Р(Нi|A) – апостериорная вероятность гипотезы Нi (насколько вероятна причина Нi с учетом факта происшедшего события А, то есть после опыта);
Итак, формула Байеса позволяет переставить причину и следствие, то есть
по известному факту события вычислить вероятность того, что оно было вызвано конкретной заданной причиной.
Р(A|Нi) – вероятность события А при истинности гипотезы Нi.
Найти:
Р(Нi|A) – апостериорная вероятность гипотезы Нi (насколько вероятна причина Нi с учетом факта происшедшего события А, то есть после опыта);
Итак, формула Байеса позволяет переставить причину и следствие, то есть
по известному факту события вычислить вероятность того, что оно было вызвано конкретной заданной причиной.
Слайд 25Пример применения формулы Байеса
По линии связи посылаются сигналы 1 и 0
с вероятностями 0,6 и 0,4.
Если посылается сигнал 1, то с вероятностями 0,9 и 0,1 принимаются сигналы 1 и 0.
Если посылается сигнал 0, то с вероятностями 0,3 и 0,7 принимаются сигналы 1 и 0.
Какова условная вероятность того, что посылается сигнал 1 при условии, что принимается сигнал 1?
Если посылается сигнал 1, то с вероятностями 0,9 и 0,1 принимаются сигналы 1 и 0.
Если посылается сигнал 0, то с вероятностями 0,3 и 0,7 принимаются сигналы 1 и 0.
Какова условная вероятность того, что посылается сигнал 1 при условии, что принимается сигнал 1?
Слайд 26Решение
Рассматриваем гипотезы:
Н1 – посылается сигнал 1; Р(Н1) = 0,6
Н2 – посылается
сигнал 0; Р(Н2) = 0,4
Рассматриваем зависимые события:
А|Н1 – принят сигнал 1 при условии, что послан сигнал 1; Р(А|Н1) = 0,9
А|Н2 – принят сигнал 1 при условии, что послан сигнал 0; Р(А|Н2) = 0,3
Н1|А – послан сигнал 1 при условии, что принят сигнал 1; Р(Н1|А) = ?
По формуле Байеса:
Рассматриваем зависимые события:
А|Н1 – принят сигнал 1 при условии, что послан сигнал 1; Р(А|Н1) = 0,9
А|Н2 – принят сигнал 1 при условии, что послан сигнал 0; Р(А|Н2) = 0,3
Н1|А – послан сигнал 1 при условии, что принят сигнал 1; Р(Н1|А) = ?
По формуле Байеса: