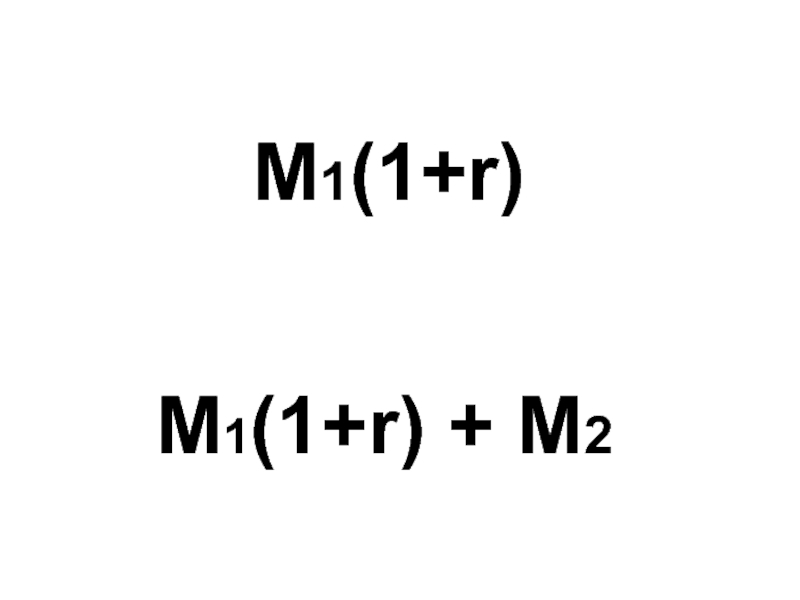- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Выбор в условиях неопределенности презентация
Содержание
- 1. Выбор в условиях неопределенности
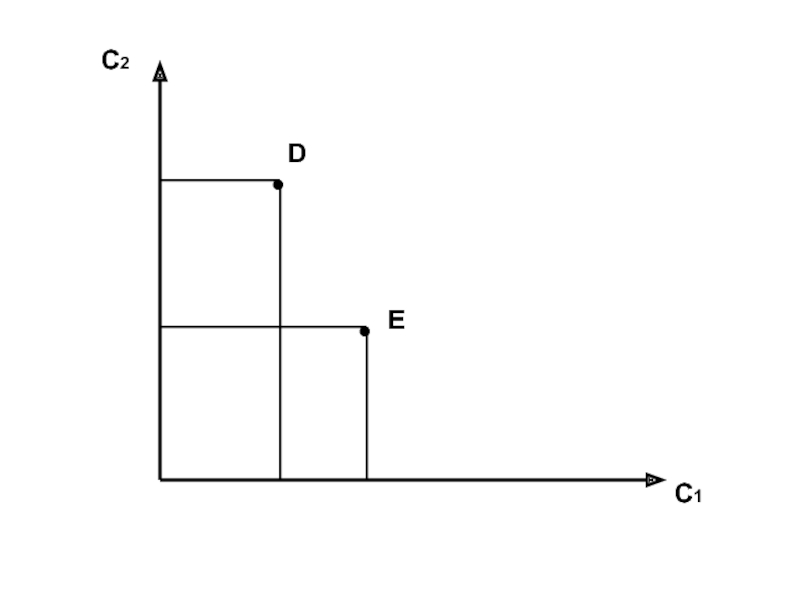
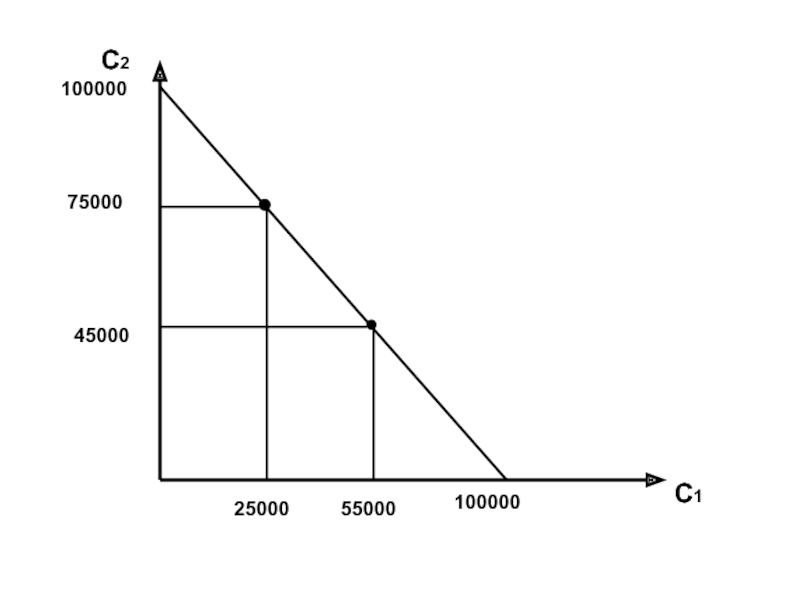
- 2. С2 С1 100000 100000 75000 25000 55000 45000
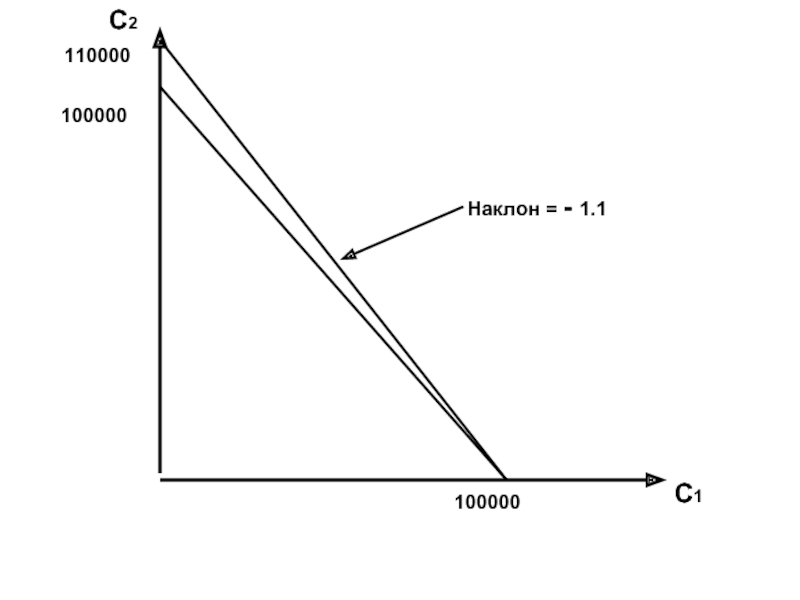
- 3. С2 С1 100000 100000 110000 Наклон = - 1.1
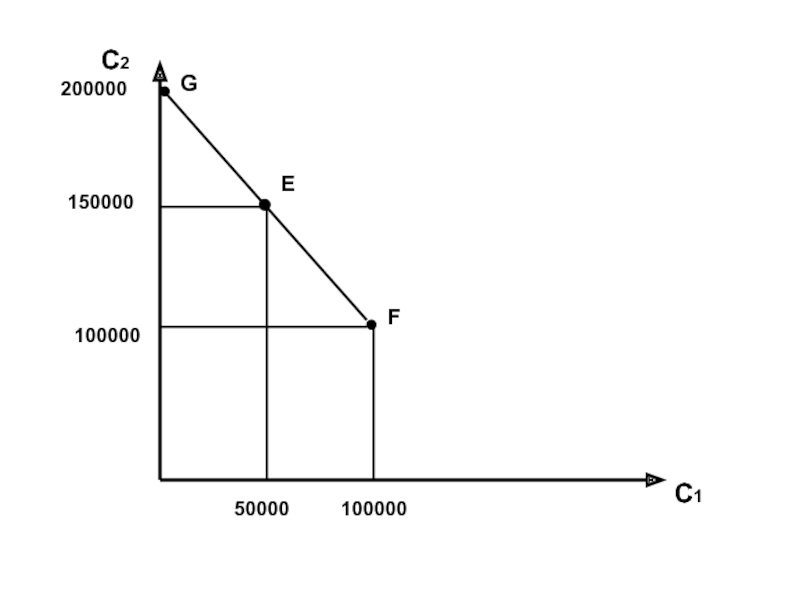
- 4. С2 С1 200000 150000 50000 100000 100000 G E F
- 5. M1(1+r) + M2 M1(1+r)
- 6. PV(M2). PV(M2)(1+r)=M2. PV(M2)= M2:(1+r.) Текущая стоимость (сегодняшняя ценность платежа)
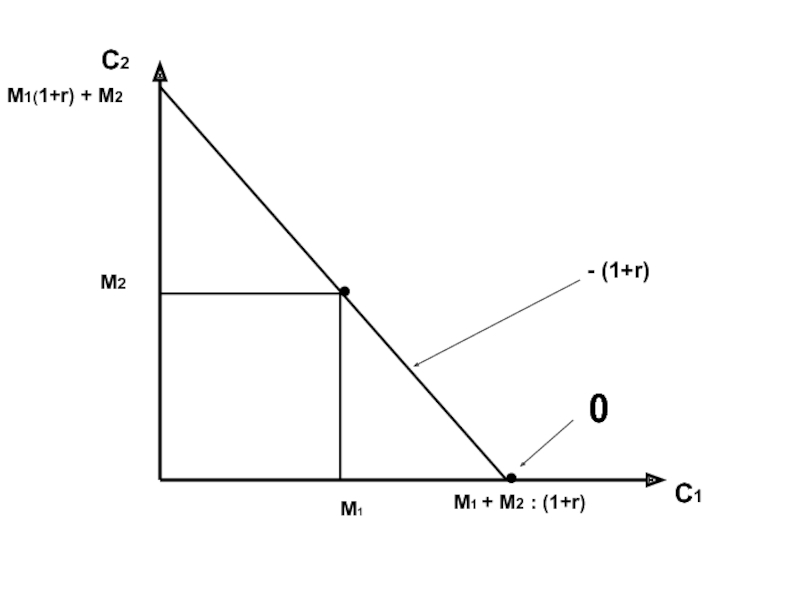
- 7. С2 С1 М1(1+r) + М2
- 8. Совершенный рынок заёмных средств – рынок, на
- 9. Критерием выбора потока дохода выступает величина текущей
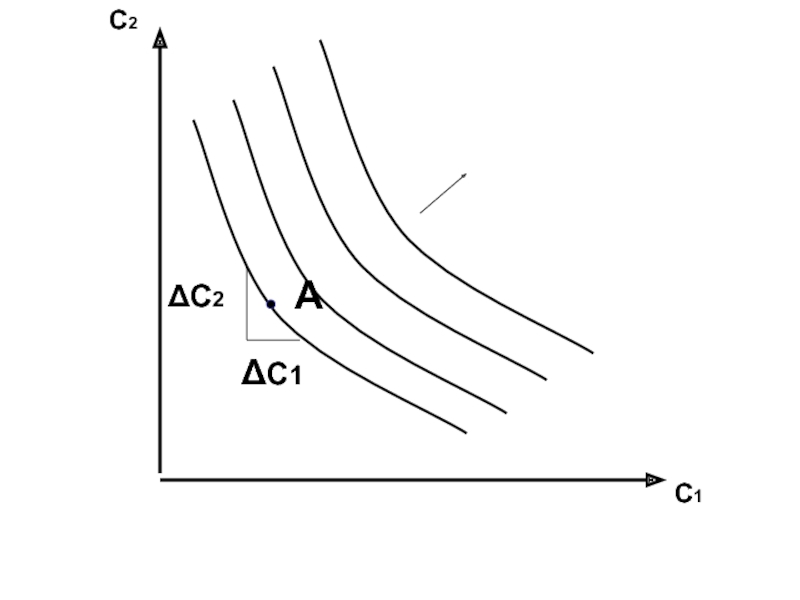
- 10. С2 С1 А ΔС2 ΔС1
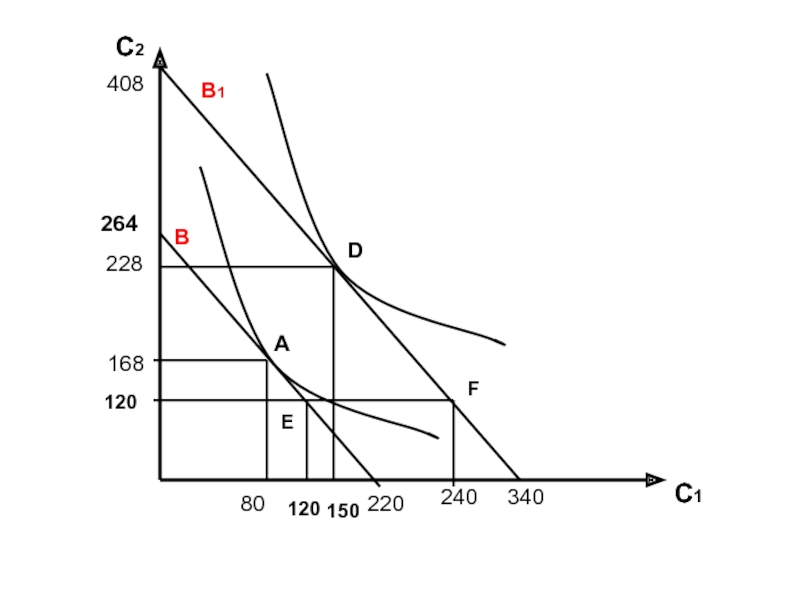
- 12. С2 С1 E F
- 13. Выбор в условиях неопределённости
- 14. Если возможно n исходов какого-либо события, сумма
- 15. Дисперсия: Стандартное отклонение: Чему равны
- 16. Актуарно справедливые игры Актуарно справедливые игры: игры
- 17. EV1 = 1/2 *100руб. + 1/2
- 18. Санкт-Петербургский парадокс: Гипотеза
- 19. EU1 = 1/2*U(M0+100) + 1/2*U(M0 - 0.5)
- 20. Риск: понятие, характеризующее изменчивость исходов в ситуации
- 21. Функция полезности фон Неймана – Моргенштерна и
- 22. Ожидаемая полезность 1-й игры: Ожидаемая полезность
- 23. Функция полезности фон Неймана – Моргенштерна и
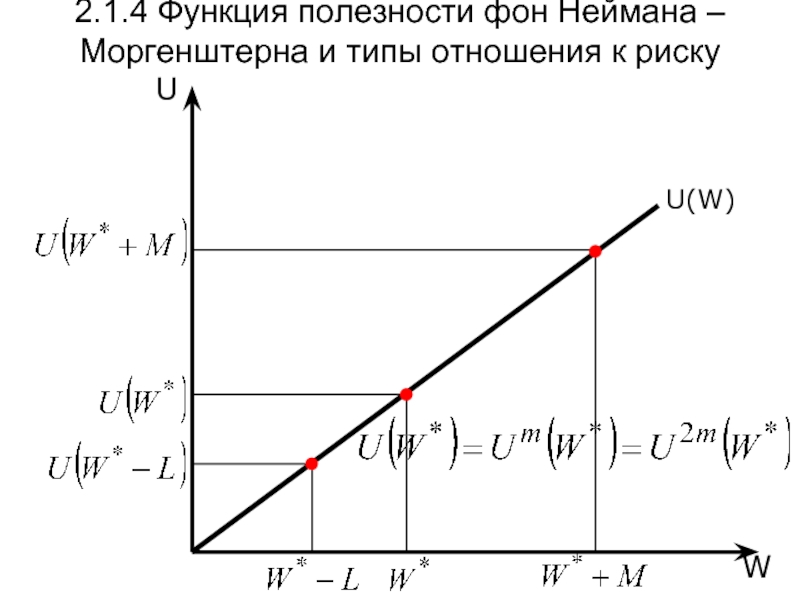
- 24. U(W) W U 2.1.4 Функция полезности фон
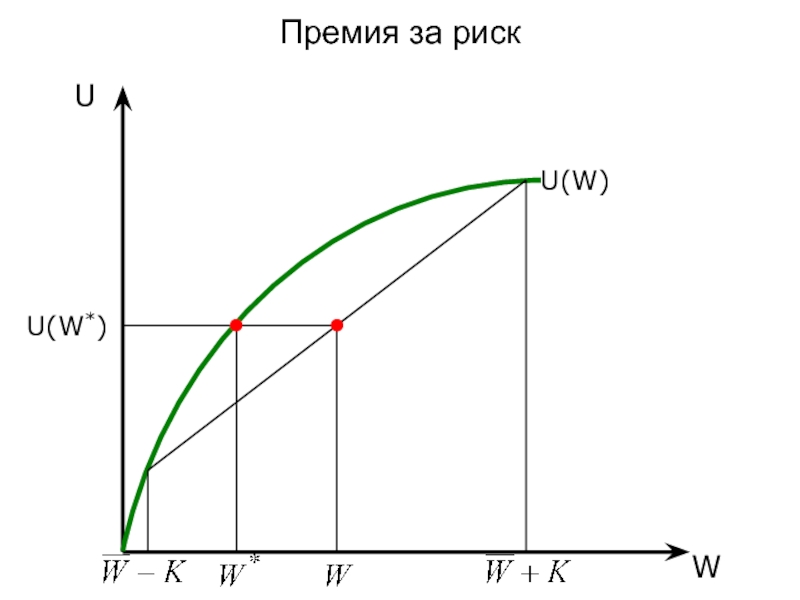
- 25. Премия за риск U(W) W U U(W*)
- 26. Наибольшее признание получила разработанная в середине 1960-х
- 27. Wg – богатство индивида при «хорошем» исходе
- 28. Wg Wb Кривые безразличия в пространстве обусловленных
- 29. Предельная норма замещения показывает пропорцию, в которой
- 30. Узел решения – точка дерева решений, в
- 31. Построение деревьев решений А
- 32. Выбор в условиях ограниченной рациональности
- 34. Проблема обязательств. (дилемма заключённого)
- 36. 2. Механизм вознаграждения 3. Проблема мимикрии. 4.
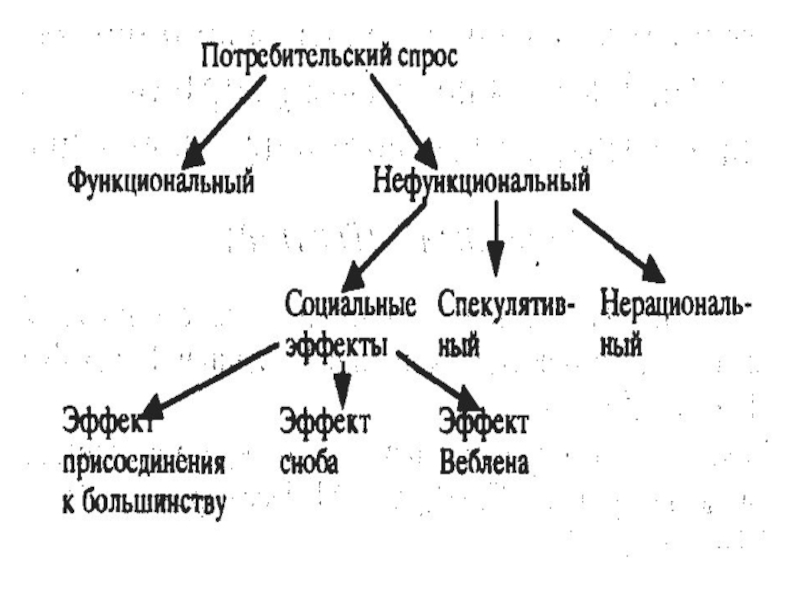
- 37. Познавательные ограничения и поведение потребителя. Ограниченная рациональность.
- 38. 6. Эвристика суждений и ошибки 7. Психофизика восприятия. 8. Трудности практических решений.
Слайд 8Совершенный рынок заёмных средств – рынок, на котором действует единая ставка
Теорема о разделении – возможность четко разделять межвременной выбор потоков доходов и межвременной выбор расходов на потребление.
*индивиды выбирают из различающихся по времени потоков доходов поток с наибольшей текущей стоимостью;
*индивиды выбирают во времени тот вариант осуществления расходов на потребление, который максимизирует их полезность при ограничении, состоящем в непревышении текущей стоимостью дохода текущей стоимости расхода на потребление.
Слайд 9Критерием выбора потока дохода выступает величина текущей стоимости (PV).
На совершенном рынке
Бессрочный аннуитет.
PV = М2 : r
Слайд 14Если возможно n исходов какого-либо события, сумма вероятностей реализации этих исходов
Ожидаемая стоимость (математическое ожидание):
Вероятность, ожидаемая стоимость и отклонения от нее
Слайд 15Дисперсия:
Стандартное отклонение:
Чему равны ожидаемая стоимость, дисперсия и стандартное отклонение, если существует
Вероятность, ожидаемая стоимость и отклонения от нее
Слайд 16Актуарно справедливые игры
Актуарно справедливые игры: игры с нулевой ожидаемой стоимостью или
Слайд 17 EV1 = 1/2 *100руб. + 1/2 *(-0.5руб.)=
EV2 =1/2*200руб. +1/2*(-100руб.)=
EV3
49.75 руб.
50 руб.
5000 руб.
Слайд 18Санкт-Петербургский парадокс:
Гипотеза ожидаемой полезности: индивиды оценивают игру не по ее ожидаемой
Гипотеза ожидаемой полезности
Слайд 20Риск: понятие, характеризующее изменчивость исходов в ситуации неопределенности.
Несклонные к риску индивиды
Склонные к риску индивиды, наоборот, выберут игру с большей изменчивостью доходности.
Функция полезности фон Неймана – Моргенштерна и типы отношения к риску
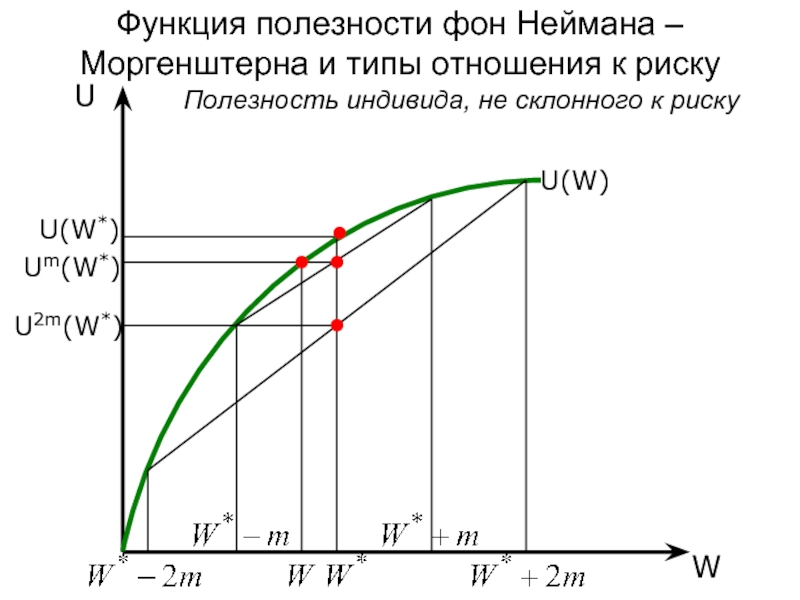
Слайд 21Функция полезности фон Неймана – Моргенштерна и типы отношения к риску
U(W)
W
U
Полезность
U(W*)
Um(W*)
U2m(W*)
Слайд 22Ожидаемая полезность 1-й игры:
Ожидаемая полезность 2-й игры:
Для несклонного к риску индивида:
Функция
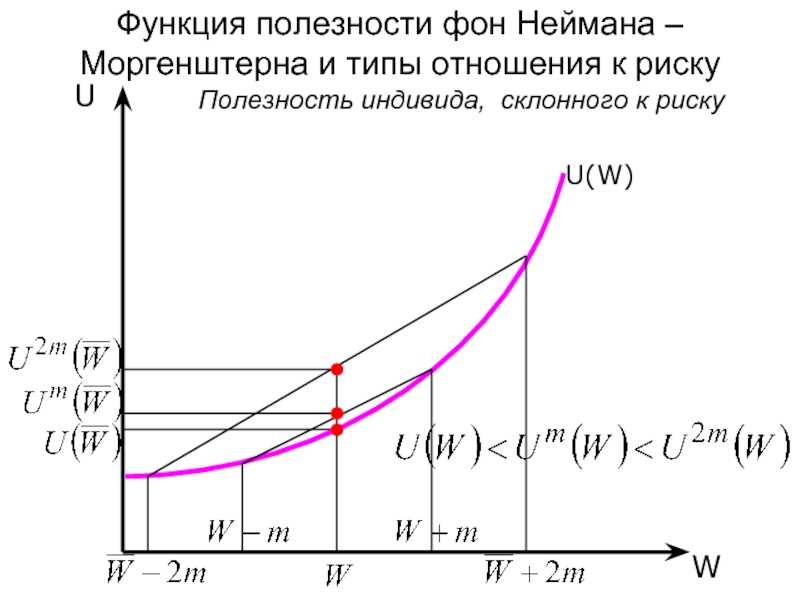
Слайд 23Функция полезности фон Неймана – Моргенштерна и типы отношения к риску
U(W)
W
U
Полезность
Слайд 26Наибольшее признание получила разработанная в середине 1960-х гг. модель оценки
долгосрочных активов
конкурентных рынках капитала в состоянии равновесия (когда все ценные бумаги и активы
оцениваются рынком верно) премия за риск инвестирования в актив) находится в прямой
зависимости от чувствительности этого актива к движению рынка
Слайд 27Wg – богатство индивида при «хорошем» исходе
Wb – богатство индивида при
Ожидаемая полезность индивида:
Вероятностные состояния как обусловленные блага
Слайд 28Wg
Wb
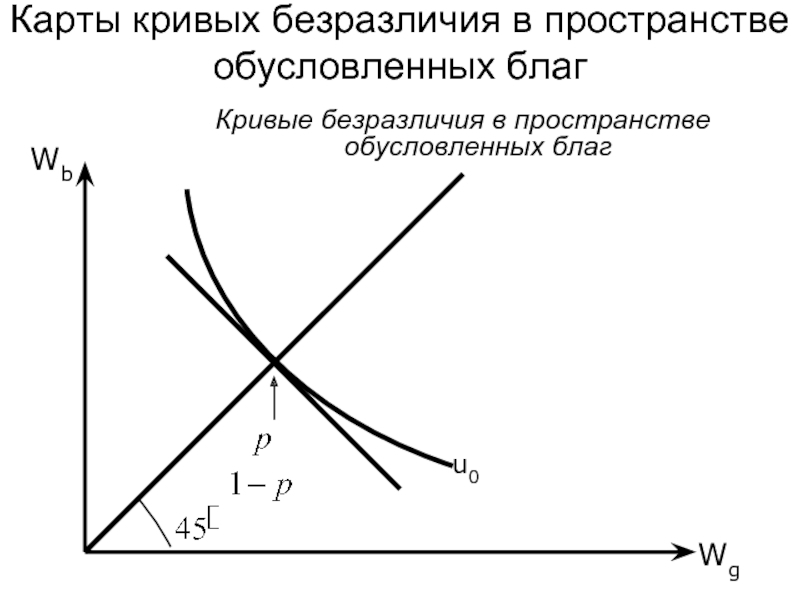
Кривые безразличия в пространстве обусловленных благ
u0
Карты кривых безразличия в пространстве
Слайд 29Предельная норма замещения показывает пропорцию, в которой индивид готов заместить товар,
При Wg=Wb:
Карты кривых безразличия в пространстве обусловленных благ
Слайд 30Узел решения – точка дерева решений, в которой индивид сталкивается с
Узел случая – точка дерева решений, движение из которой по исходящим ветвям обусловлено случайным процессом.
Конечный узел – точка дерева решений, представляющая конечный исход, связываемый с данной ветвью дерева решений.
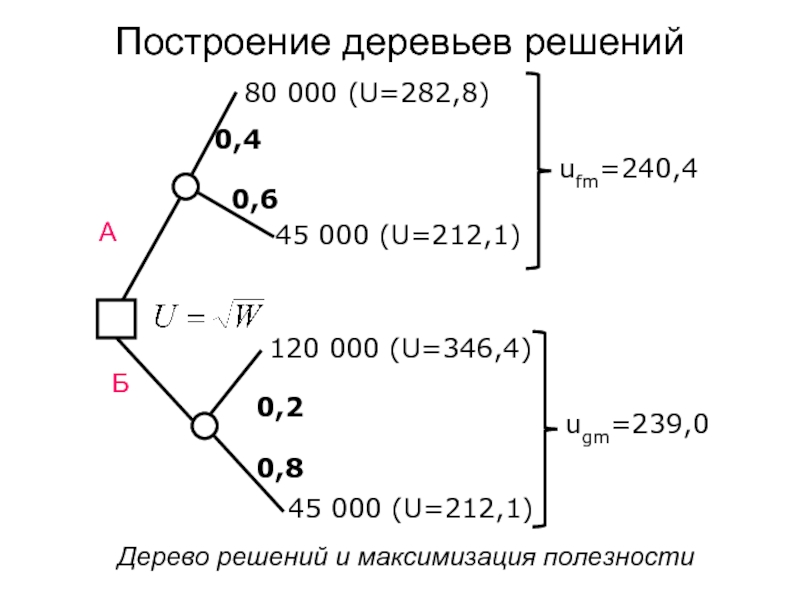
Построение деревьев решений
Слайд 31Построение деревьев решений
А
Б
Дерево решений и максимизация полезности
0,6
0,8
0,2
0,4
80 000 (U=282,8)
45 000
120 000 (U=346,4)
45 000 (U=212,1)
ufm=240,4
ugm=239,0
Слайд 362. Механизм вознаграждения
3. Проблема мимикрии.
4. Различие вкусов.
5. Альтруистические предпочтения
6. Забота о
Слайд 37Познавательные ограничения и поведение потребителя.
Ограниченная рациональность.
Асимметричная функция ценности.
Невозвратные издержки.
Прямые и вменённые
Гедоническое «обрамление»