- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Векторы в пространстве. (10-11 класс) презентация
Содержание
- 1. Векторы в пространстве. (10-11 класс)
- 2. Отрезок, для которого указано,
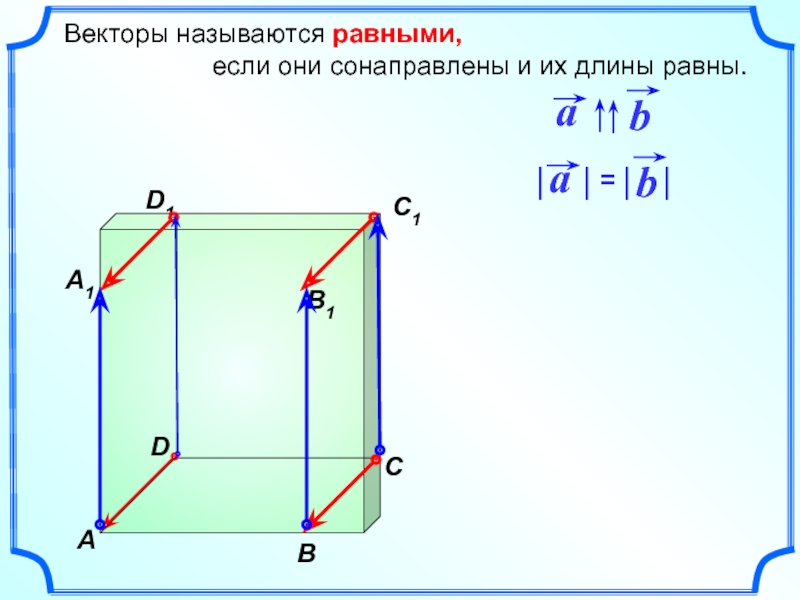
- 3. Два ненулевых вектора
- 4. Два ненулевых вектора
- 5. Многие физические величины, например сила
- 6. Электрический ток, т.е. направленное
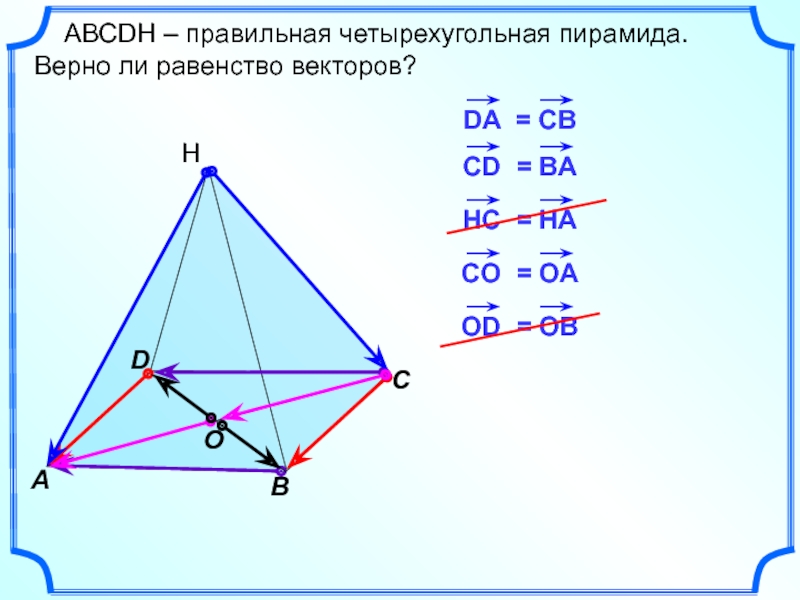
- 8. D А АВСDH –
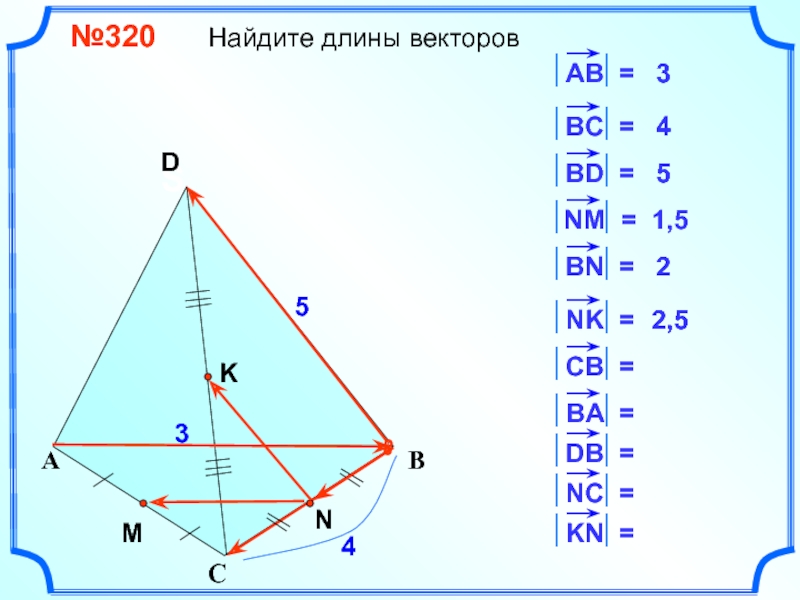
- 9. №320
- 10. №322 На рисунке
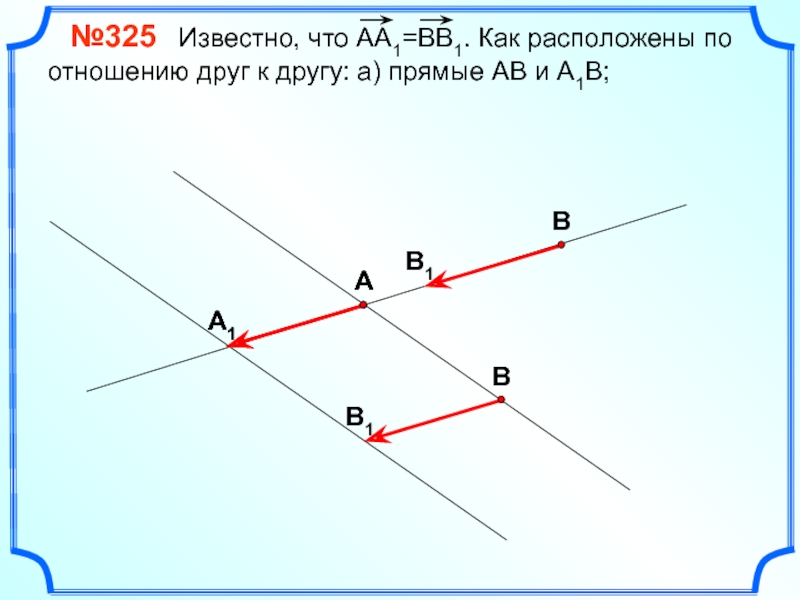
- 11. №325 Известно, что
- 12. №325
- 13. №325 Известно, что
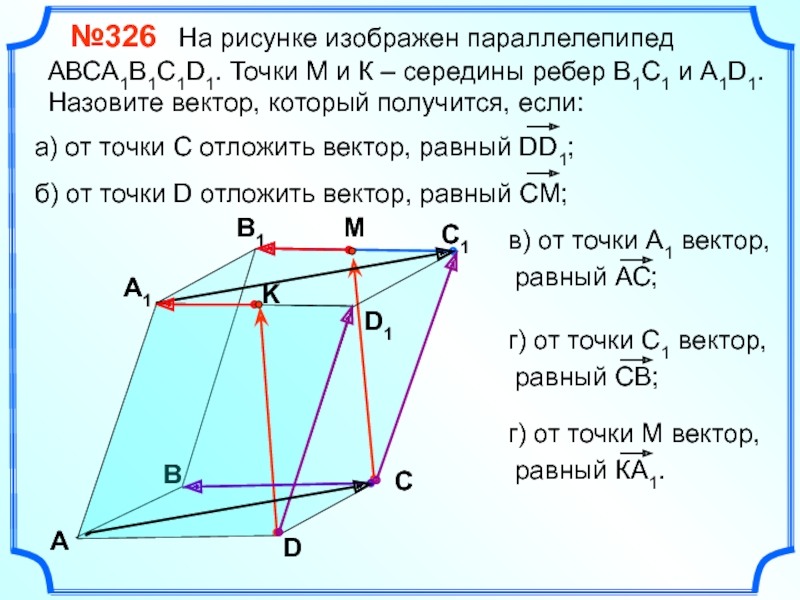
- 14. №326 На
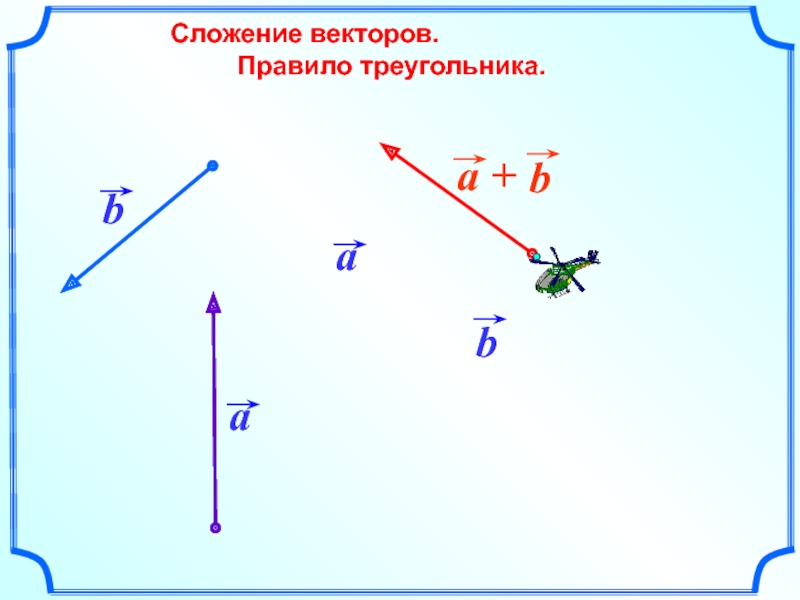
- 15. Сложение векторов.
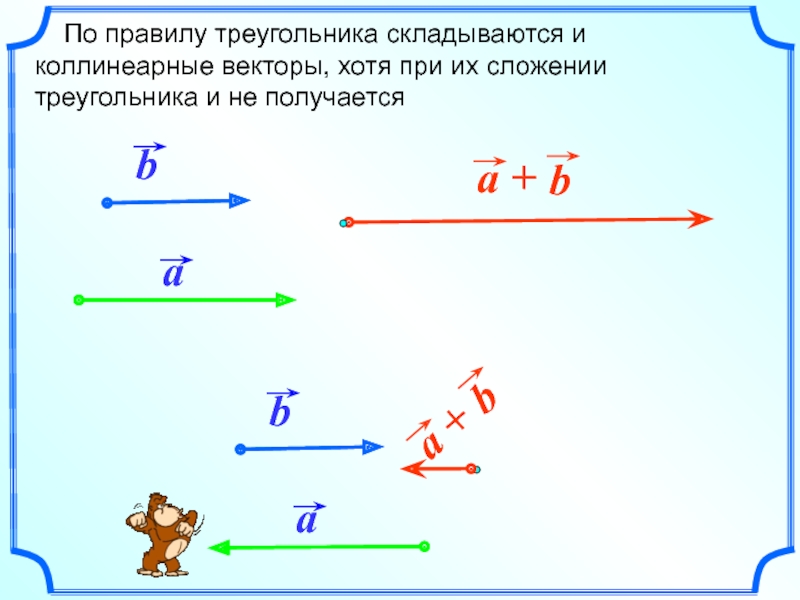
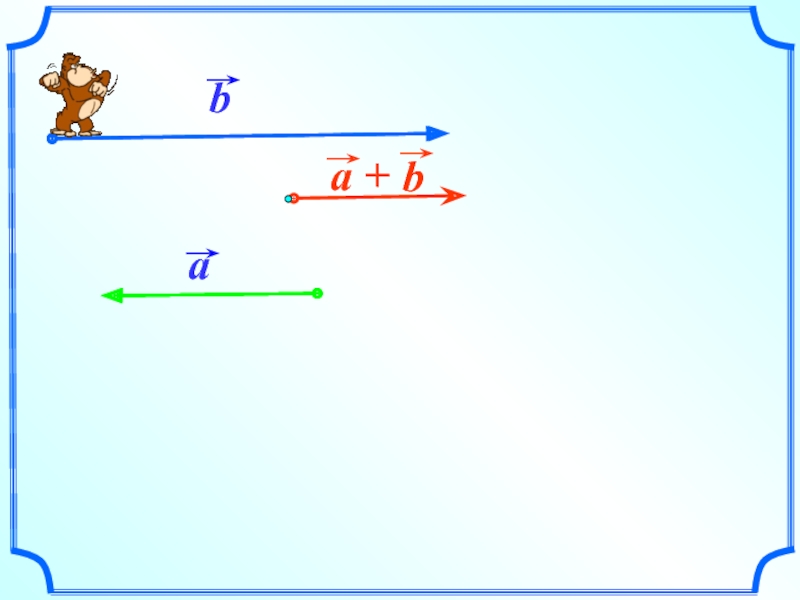
- 16. По правилу треугольника складываются
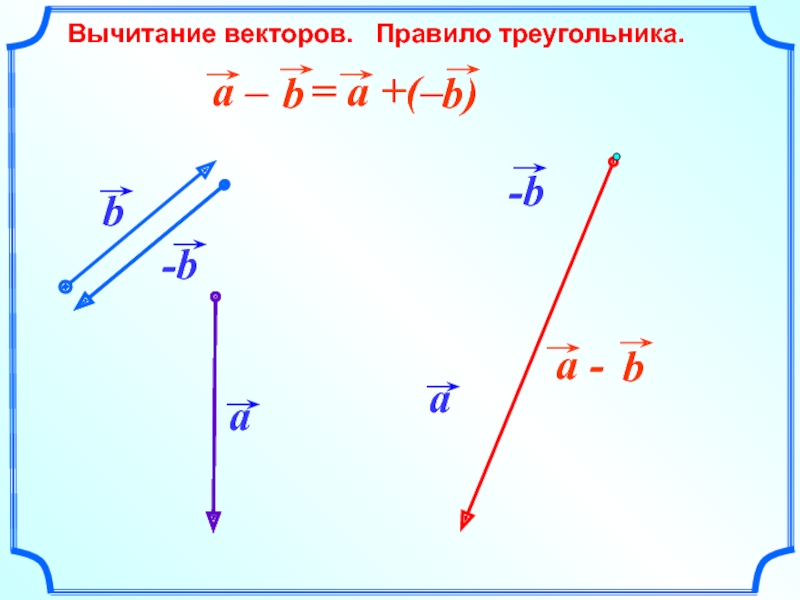
- 18. Вычитание векторов. Правило треугольника.
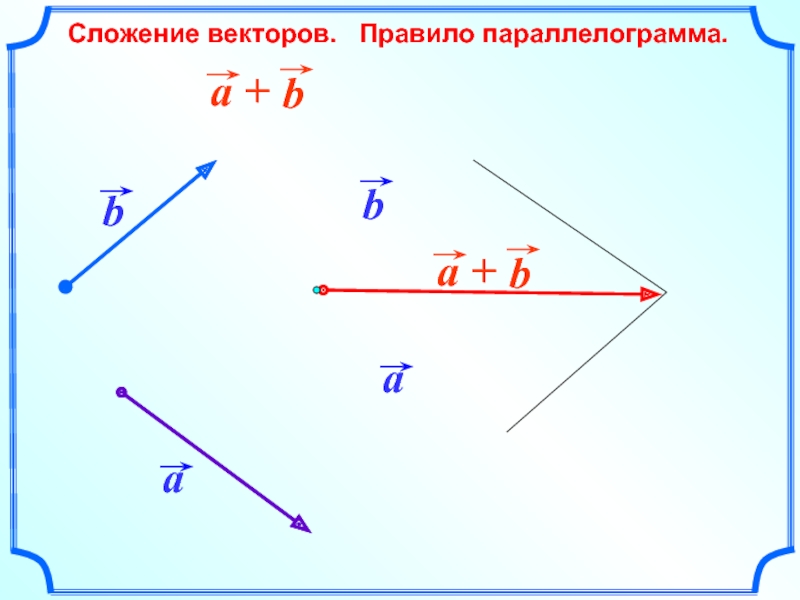
- 19. Сложение векторов. Правило параллелограмма.
- 20. Сложение векторов.
- 21. Сложение векторов. Правило треугольника. АС =
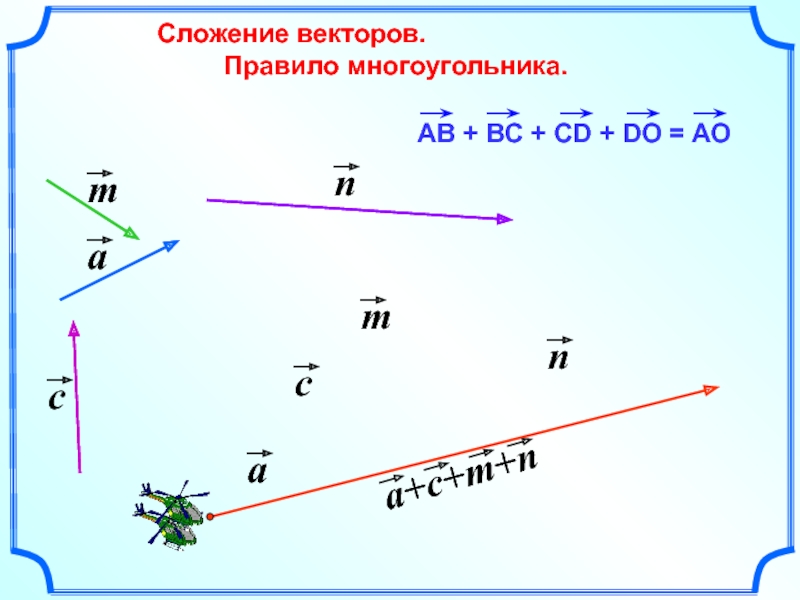
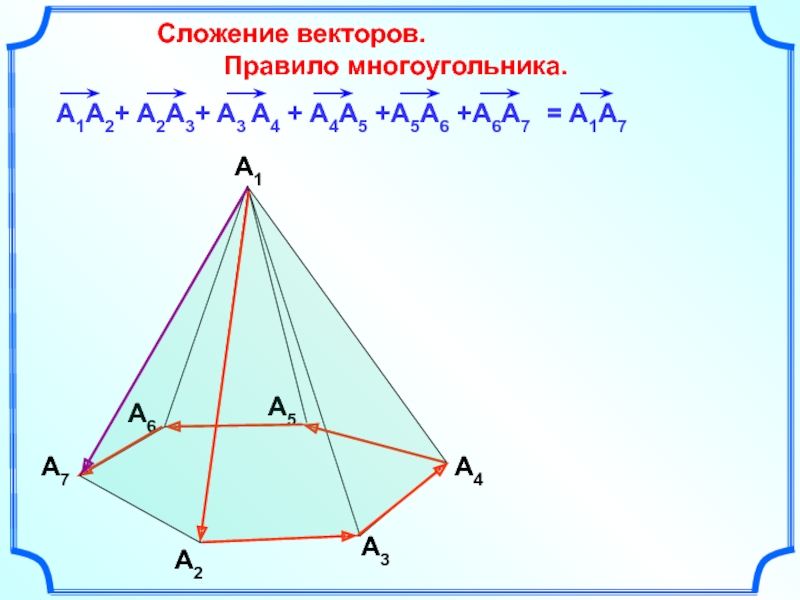
- 22. Сложение векторов. Правило многоугольника.
- 23. Сложение векторов.
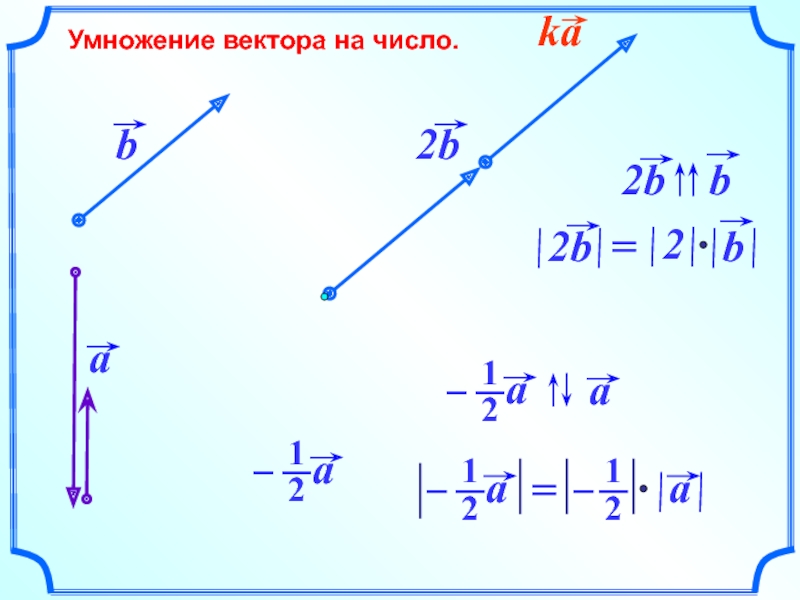
- 24. Умножение вектора на число.
- 25. Умножение вектора на число.
- 26. Умножение вектора на число. Произведение любого вектора
- 27. АВ =
- 28. Диагонали параллелепипеда АВСDА1В1С1D1
Отрезок, для которого указано, какой из его концов считается началом, а какой концом, называется вектором
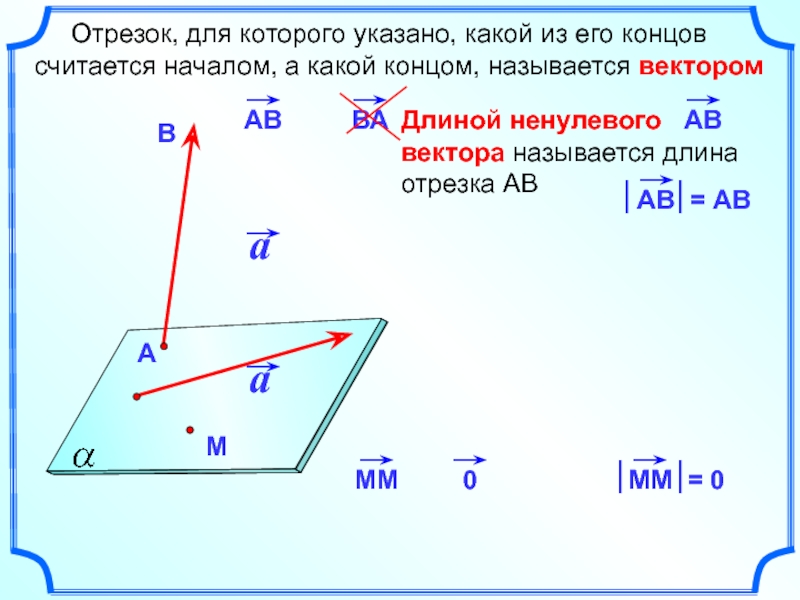
Слайд 2 Отрезок, для которого указано, какой из его концов
считается началом, а какой концом, называется вектором
Слайд 3
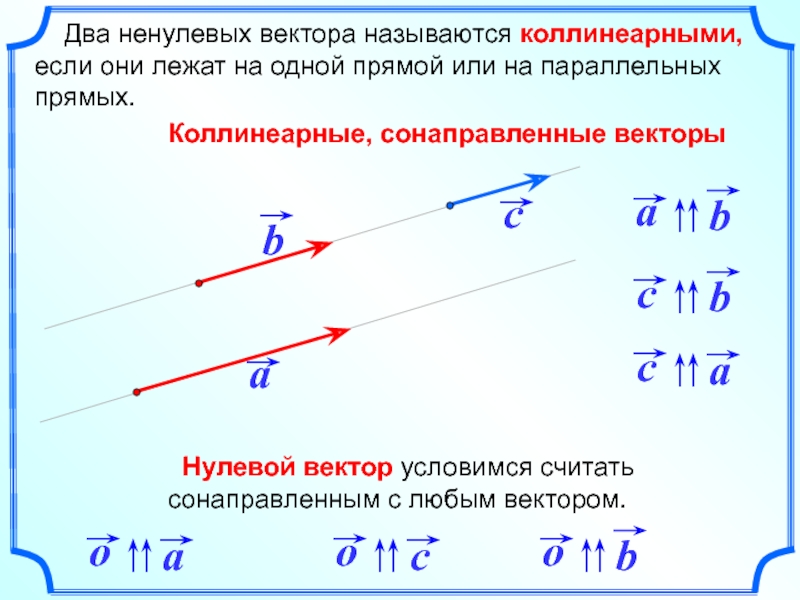
Два ненулевых вектора называются коллинеарными, если они лежат на
одной прямой или на параллельных прямых.
Коллинеарные, сонаправленные векторы
Нулевой вектор условимся считать сонаправленным с любым вектором.
Слайд 4
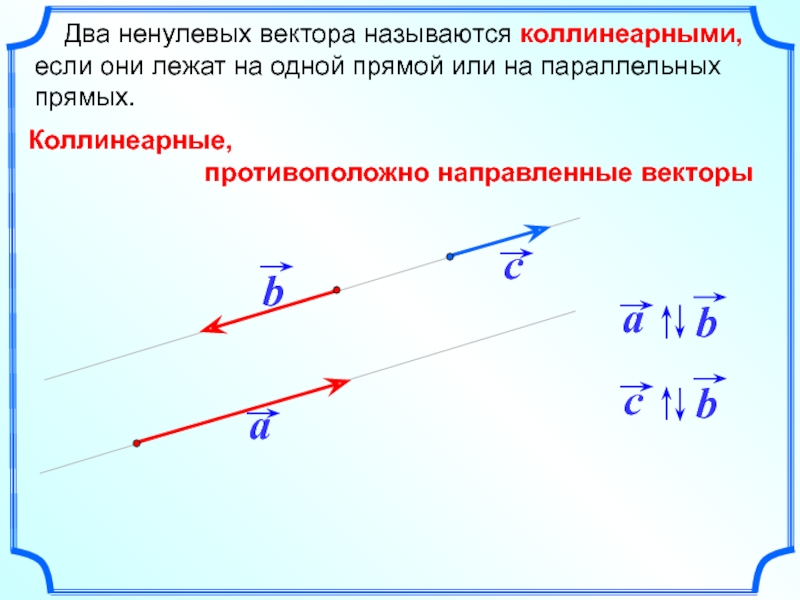
Два ненулевых вектора называются коллинеарными, если они лежат на
одной прямой или на параллельных прямых.
Коллинеарные,
противоположно направленные векторы
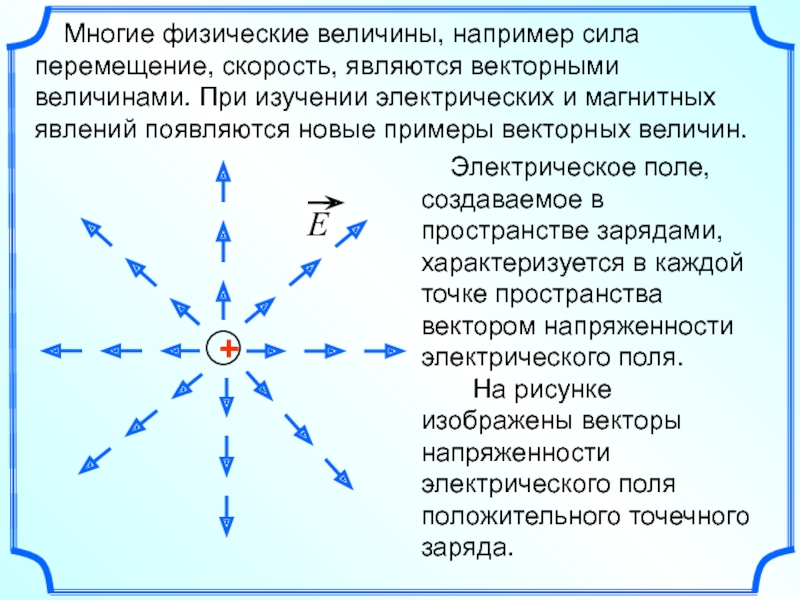
Слайд 5 Многие физические величины, например сила перемещение, скорость, являются векторными
величинами. При изучении электрических и магнитных явлений появляются новые примеры векторных величин.
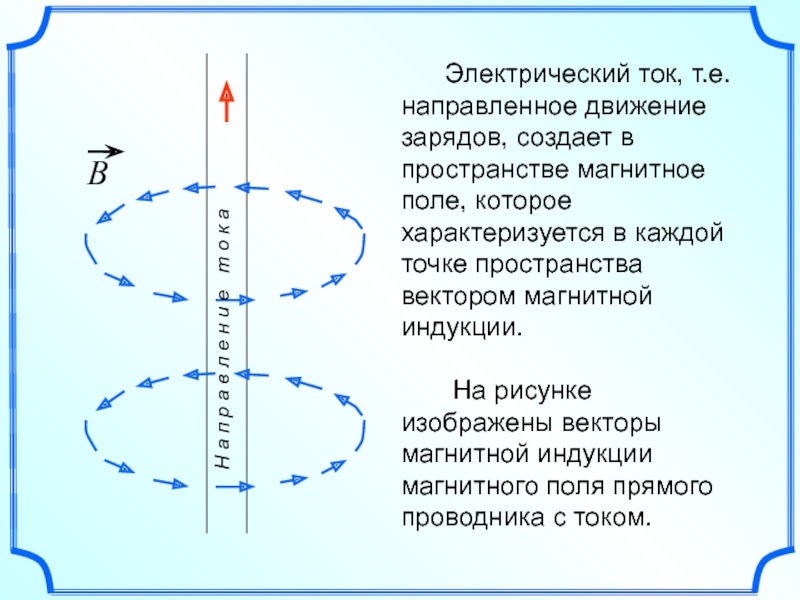
Слайд 6 Электрический ток, т.е. направленное движение зарядов, создает в
пространстве магнитное поле, которое характеризуется в каждой точке пространства вектором магнитной индукции.
На рисунке изображены векторы магнитной индукции магнитного поля прямого проводника с током.
На рисунке изображены векторы магнитной индукции магнитного поля прямого проводника с током.
Слайд 10
№322 На рисунке изображен параллелепипед АВСA1B1C1D1. Точки М
и К – середины ребер В1С1 и А1D1. Укажите на этом рисунке все пары: а) сонаправленных векторов; б) противоположно направленных векторов; в) равных векторов.
В
А
В1
С1
D1
D
С
K
А1
M
Слайд 12
№325 Известно, что АА1=ВВ1. Как расположены по
отношению друг к другу:
б) прямая АВ и плоскость, проходящая через точки А1 и В1;
б) прямая АВ и плоскость, проходящая через точки А1 и В1;
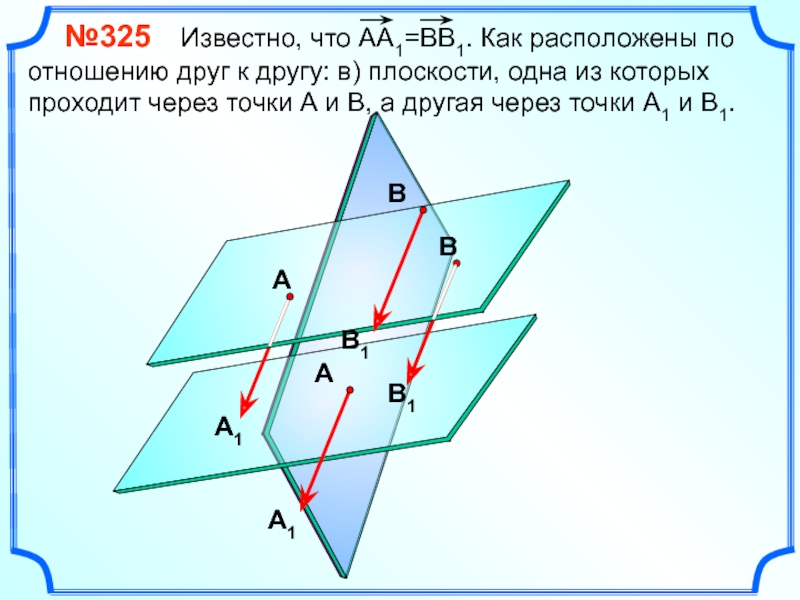
Слайд 13 №325 Известно, что АА1=ВВ1. Как расположены по
отношению друг к другу: в) плоскости, одна из которых проходит через точки А и В, а другая через точки А1 и В1.
А
В
Слайд 14
№326 На рисунке изображен параллелепипед АВСA1B1C1D1. Точки М
и К – середины ребер В1С1 и А1D1. Назовите вектор, который получится, если:
В
А
В1
С1
D1
D
С
K
А1
M
Слайд 16
По правилу треугольника складываются и коллинеарные векторы, хотя при
их сложении треугольника и не получается
Слайд 26Умножение вектора на число.
Произведение любого вектора на число нуль есть нулевой
вектор.
Сочетательный закон
Первый распределительный закон
Второй распределительный закон
Произведение нулевого вектора на любое число считается нулевой вектор.
Слайд 27
АВ = СD
k
A
B
C
A1
B1
C1
D1
D
№344
Диагонали куба АВСDА1В1С1D1 пересекаются
в точке О. Найдите число k такое, чтобы равенства были верны.
в точке О. Найдите число k такое, чтобы равенства были верны.
АC1 = AO
k
O
OD1 = D1B
k
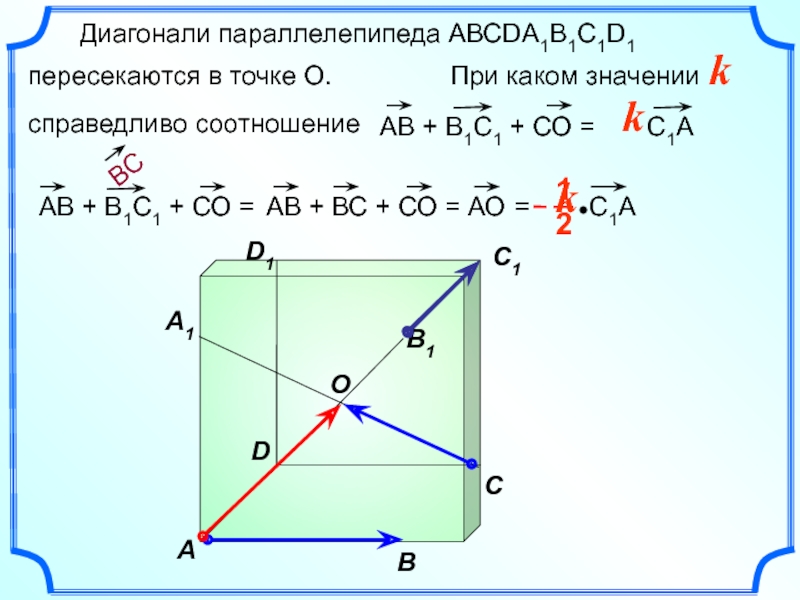
Слайд 28 Диагонали параллелепипеда АВСDА1В1С1D1
пересекаются в точке О.
При каком значении
справедливо соотношение
справедливо соотношение
k
A
B
C
A1
B1
C1
D1
D
O
k
АВ + В1С1 + СО = С1A
k
