- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Обернена тригонометрична функція y=arcsinx презентация
Содержание
- 1. Обернена тригонометрична функція y=arcsinx
- 2. Це означає: Функція у = sin
- 3. Утворення функції оберненої до у = sin
- 4. Графік функції у = arcsin
- 5. 1. Область визначення
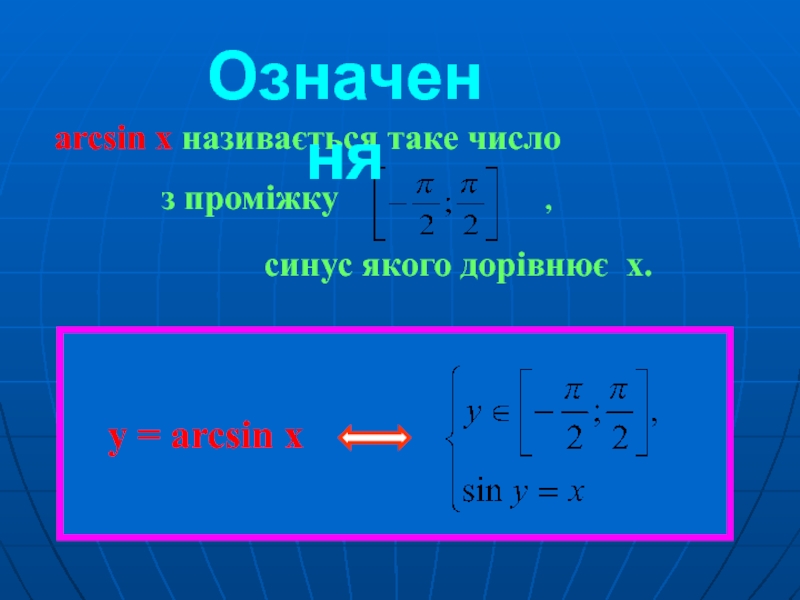
- 6. arcsin x називається таке число
- 7. 1. Для яких значень змінної х визначений
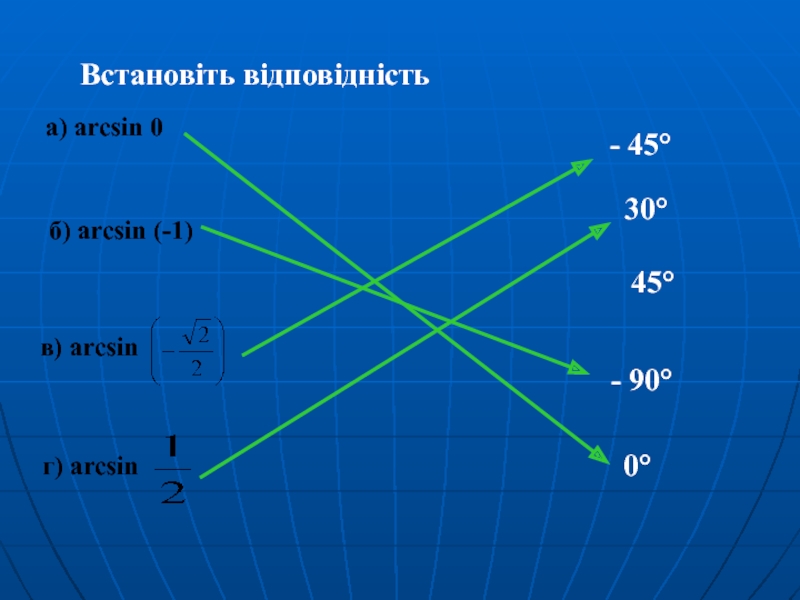
- 8. Встановіть відповідність а) arcsin 0 в) arcsin
- 9. 3. У якій чверті лежить кожен із
- 10. Перетворення графіків функцій
- 11. y = arcsin x ± n
- 12. y = arcsin (x ± а)
- 13. y = - arcsin x Для
- 14. y = arcsin (- x) y
- 15. y = k·arcsin x Для побудови
- 16. Для побудови графіка функції y = |arcsin
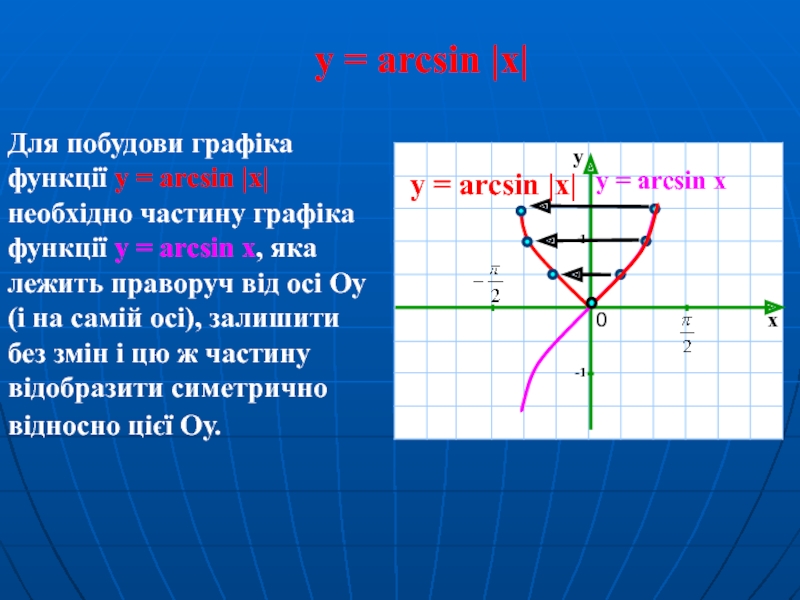
- 17. y = arcsin |x| Для побудови
- 18. Перевір себе 1. Серед наведених функцій вкажіть
- 19. Побудуйте графік функції y = 2 -
Слайд 1Обернена тригонометрична функція
y = arcsin x
Підготували:
Бушина Інна Борисівна, вчитель математики та
Павліченко Світлана Петрівна, вчитель математики ЗОШ № 10 м. Черкаси , друга категорія
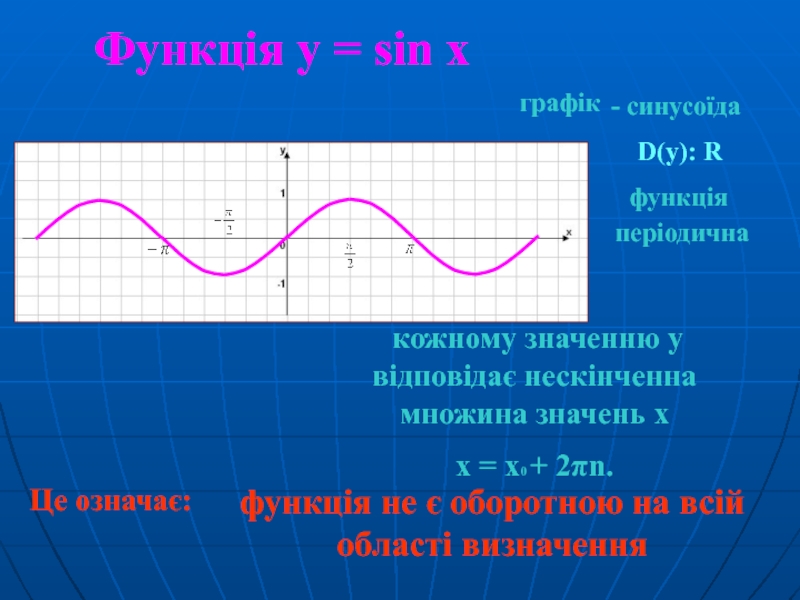
Слайд 2Це означає:
Функція у = sin x
кожному значенню у
х = х0 + 2πn.
графік
- синусоїда
функція не є оборотною на всій області визначення
D(у): R
функція
періодична
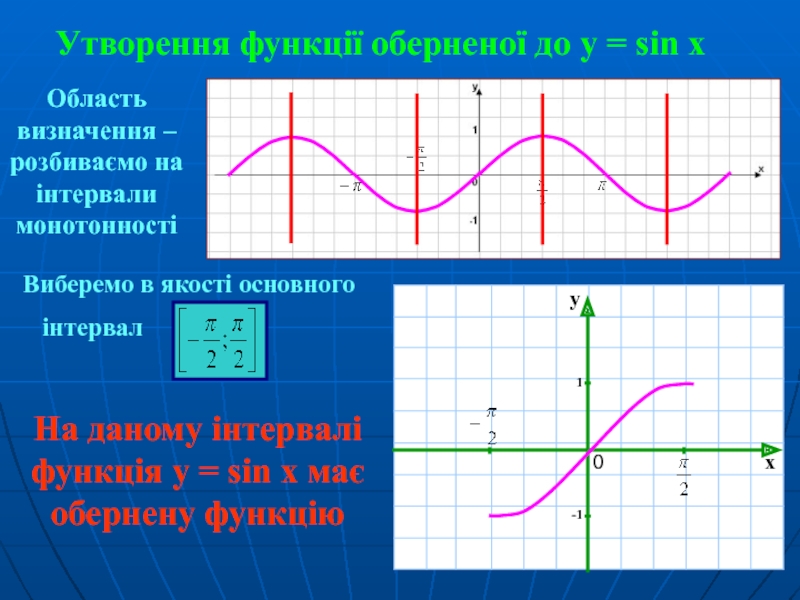
Слайд 3Утворення функції оберненої до у = sin x
Виберемо в якості основного
інтервал
Область визначення – розбиваємо на інтервали монотонності
На даному інтервалі функція у = sin x має обернену функцію
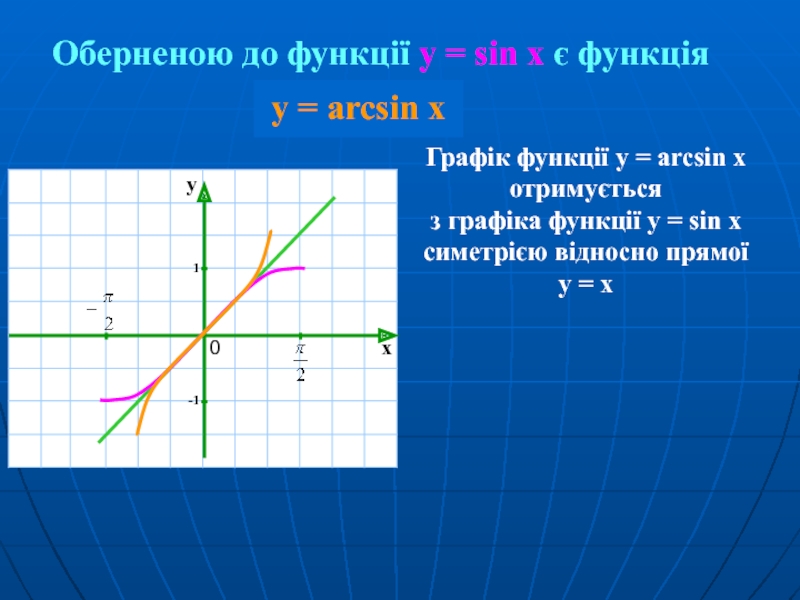
Слайд 4
Графік функції у = arcsin x отримується
Оберненою до функції y = sin x є функція
у = arcsin x
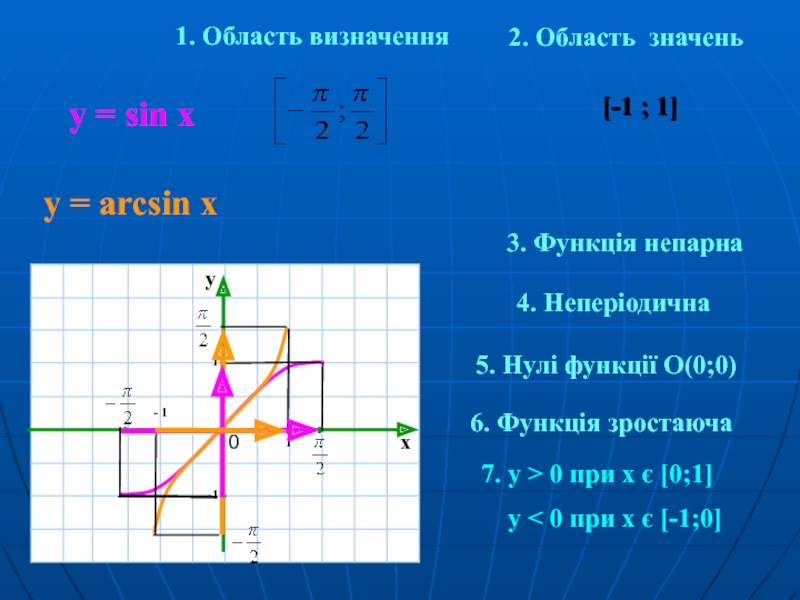
Слайд 51. Область визначення
у =
у = arcsin x
[-1 ; 1]
2. Область значень
1
- 1
[-1 ; 1]
3. Функція непарна
4. Неперіодична
5. Нулі функції O(0;0)
6. Функція зростаюча
7. y > 0 при х є [0;1]
y < 0 при х є [-1;0]
Слайд 71. Для яких значень змінної х визначений вираз arcsin х ?
А)
Б) -1 ≤ х ≤ 1.
В) - ∞ < х < ∞ .
Г) -1 < х < 1.
2. Для яких значень змінної х визначений вираз arcsin (х – 2) ?
А) -1 ≤ х ≤ -1.
Б) - ∞ < х < ∞ .
В) 1 ≤ х ≤ 3.
Г) -3 ≤ х ≤ -1.
Перевір себе
Слайд 93. У якій чверті лежить кожен із кутів:
1) arcsin 0,7
2) arcsin (-0,35)
А) І.
Б) ІІ.
Г) ІV.
В) ІІІ.
4. Обчисліть :
1) arcsin
2) arcsin + arcsin
А) .
Б) 2π .
В) .
Г) π .
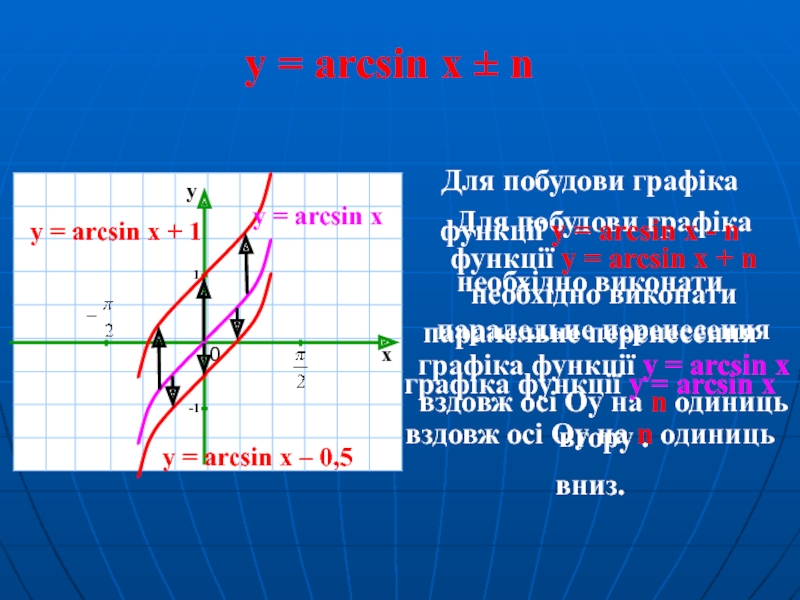
Слайд 11y = arcsin x ± n
y = arcsin x
Для побудови
y = arcsin x + 1
Для побудови графіка
функції y = arcsin x - n
необхідно виконати
паралельне перенесення
графіка функції y = arcsin x
вздовж осі Oy на n одиниць
вниз.
y = arcsin x – 0,5
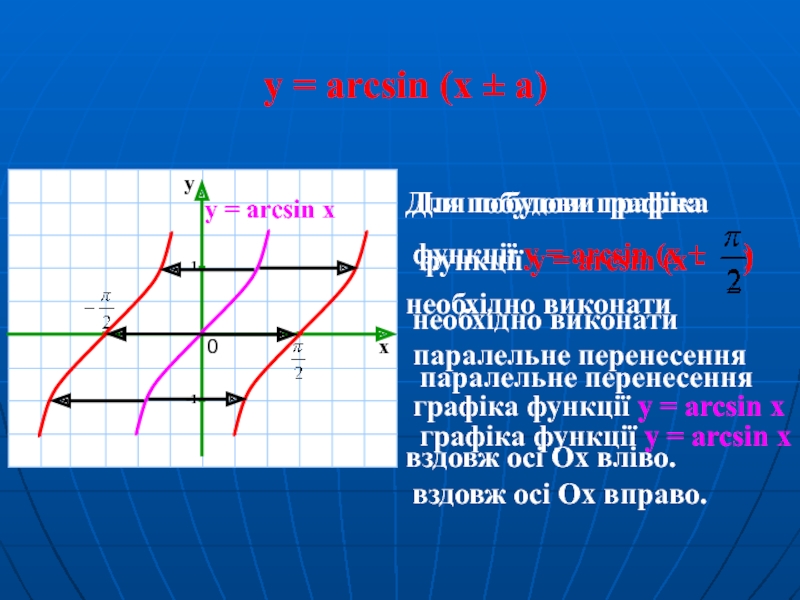
Слайд 12y = arcsin (x ± а)
Для побудови графіка
функції y
необхідно виконати
паралельне перенесення
графіка функції y = arcsin x
вздовж осі Oх вліво.
y = arcsin x
Для побудови графіка
функції y = arcsin (x - )
необхідно виконати
паралельне перенесення
графіка функції y = arcsin x
вздовж осі Oх вправо.
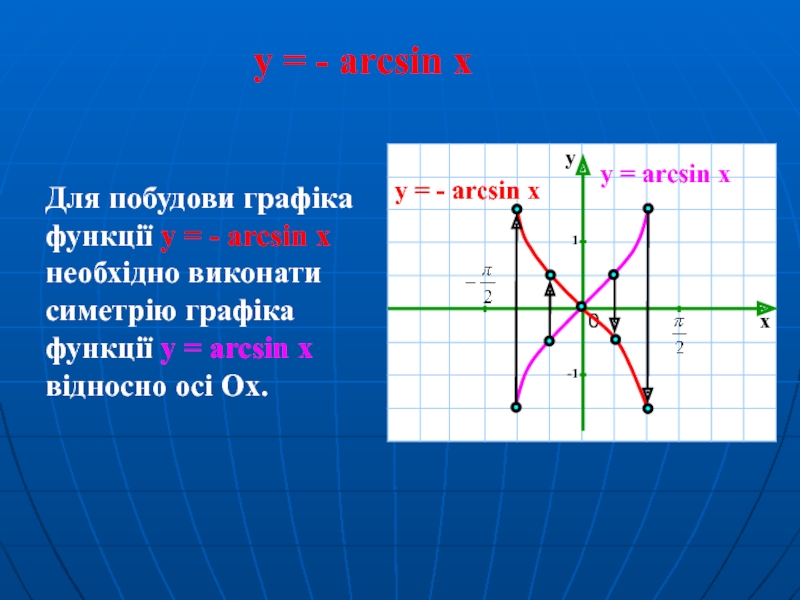
Слайд 13y = - arcsin x
Для побудови графіка функції y =
y = arcsin x
y = - arcsin x
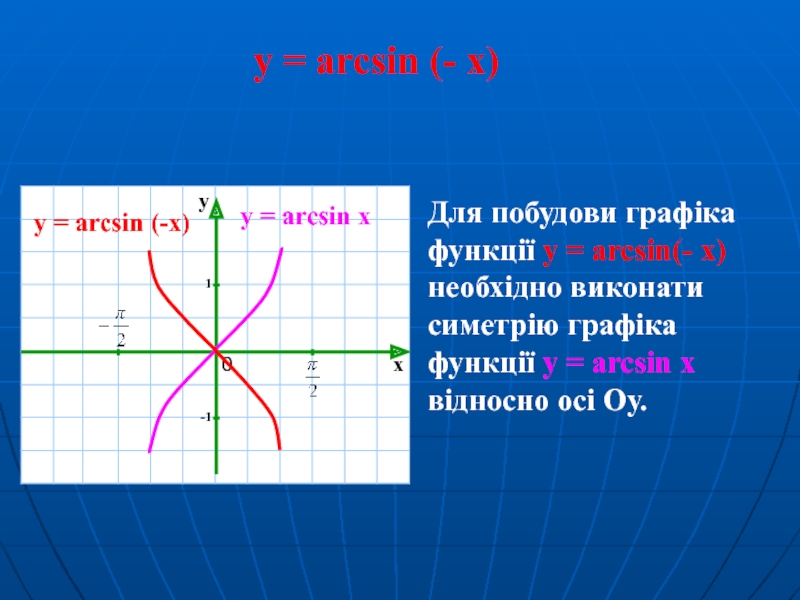
Слайд 14y = arcsin (- x)
y = arcsin x
Для побудови графіка
y = arcsin (-x)
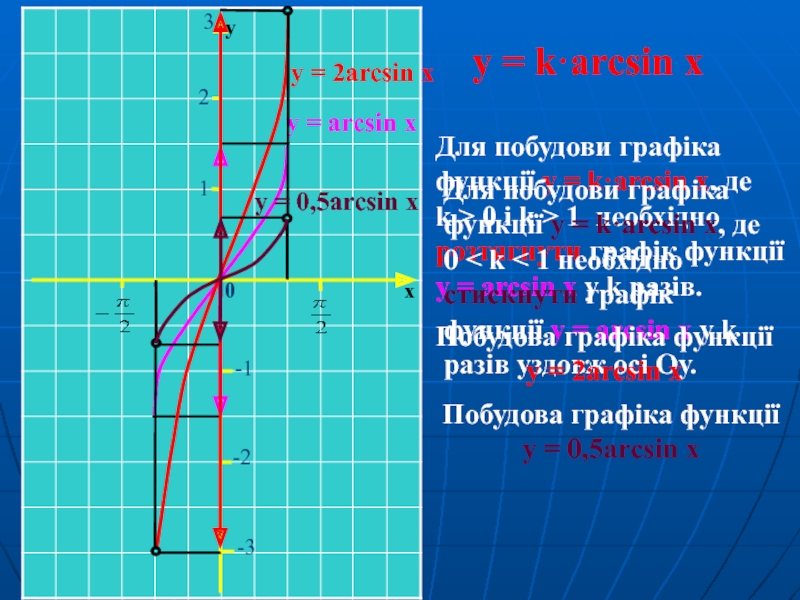
Слайд 15y = k·arcsin x
Для побудови графіка функції y = k·arcsin
Для побудови графіка функції y = k·arcsin x, де 0 < k < 1 необхідно стискнути графік функції y = arcsin x у k разів уздовж осі Oу.
0
-1
1
2
-2
х
у
y = arcsin x
y = 2arcsin x
-3
3
Побудова графіка функції у = 2arcsin x
Побудова графіка функції у = 0,5arcsin x
у = 0,5arcsin x
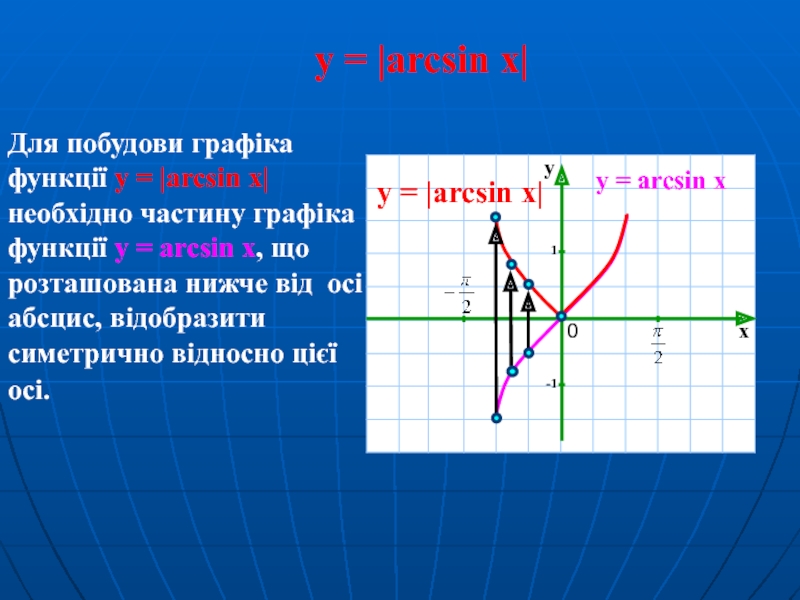
Слайд 16Для побудови графіка функції y = |arcsin x| необхідно частину графіка
y = |arcsin x|
y = arcsin x
y = |arcsin x|
Слайд 17y = arcsin |x|
Для побудови графіка функції y = arcsin
y = arcsin x
y = arcsin |x|
Слайд 18Перевір себе
1. Серед наведених функцій вкажіть спадну:
а) у = arcsin x
б) у = arcsin (x + 2)
в) у = - arcsin х
г) у = |arcsin x|
2. Серед наведених вкажіть функцію, графік якої
паралельно перенесли на 2 одиниці вниз вздовж осі Oy і
на 7 одиниць вліво вздовж осі Ox.
б) у = arcsin (x + 7) - 2
а) у = arcsin x + 2
в) у = arcsin (x - 7) - 2
г) у = arcsin (x - 2) - 7
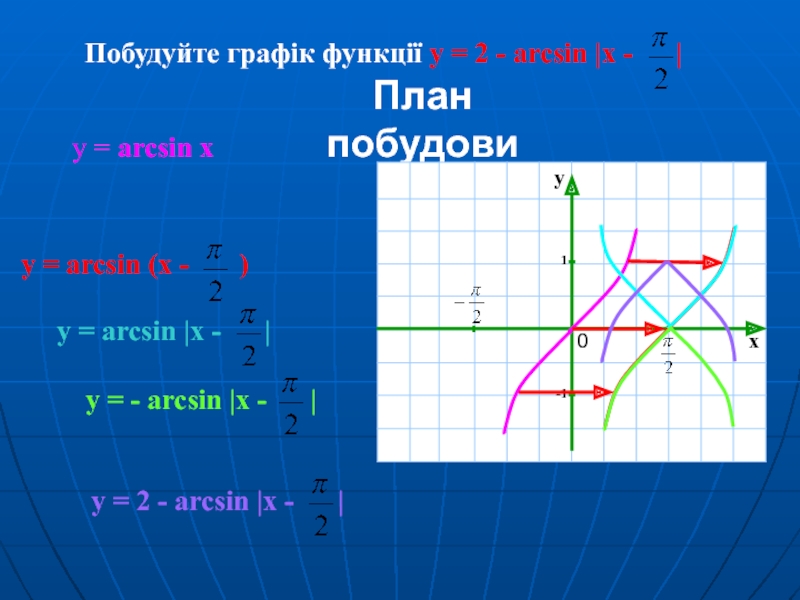
Слайд 19Побудуйте графік функції y = 2 - arcsin |x -
План побудови
y = arcsin (x - )
y = arcsin |x - |
y = - arcsin |x - |
y = 2 - arcsin |x - |
у = arcsin x