- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Векторы на плоскости и в пространстве. Основные понятия презентация
Содержание
- 1. Векторы на плоскости и в пространстве. Основные понятия
- 2. Понятие вектора в пространстве Вектор(направленный отрезок) –
- 3. Нулевым вектором называется вектор, начало и
- 4. Коллинеарные векторы Среди коллинеарных различают: Сонаправленные векторы Противоположно направленные векторы
- 5. Равные векторы Равные векторы - сонаправленные векторы,
- 6. Противоположные векторы Противоположные векторы – противоположно направленные
- 7. Признак коллинеарности
- 8. Действия с векторами Сложение Вычитание Умножение вектора на число
- 9. Сложение векторов Правило треугольника Правило параллелограмма Правило многоугольника Правило параллелепипеда
- 10. Правило треугольника А B C
- 11. Правило треугольника А B C Для
- 12. Правило параллелограмма А B C
- 13. Правило многоугольника Сумма векторов равна вектору, проведенному
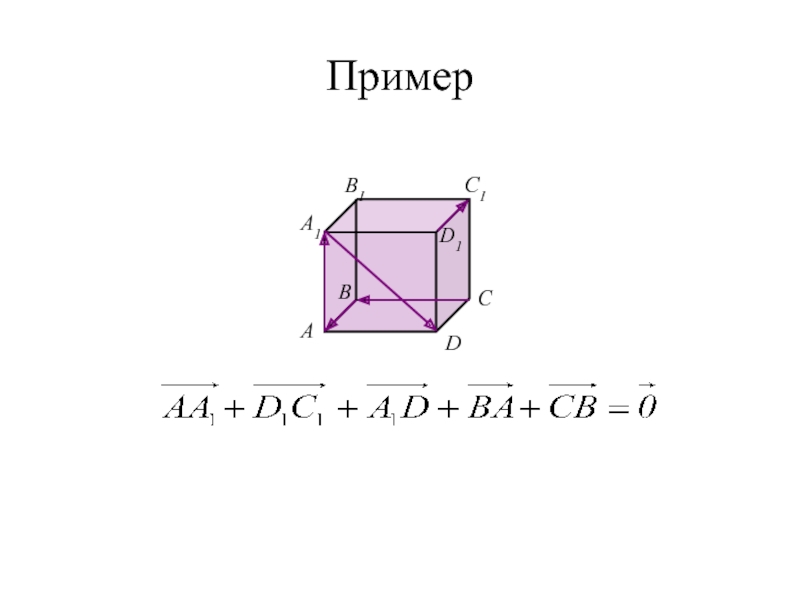
- 14. Пример C A B D A1 B1 C1 D1
- 15. Правило параллелепипеда B А C D
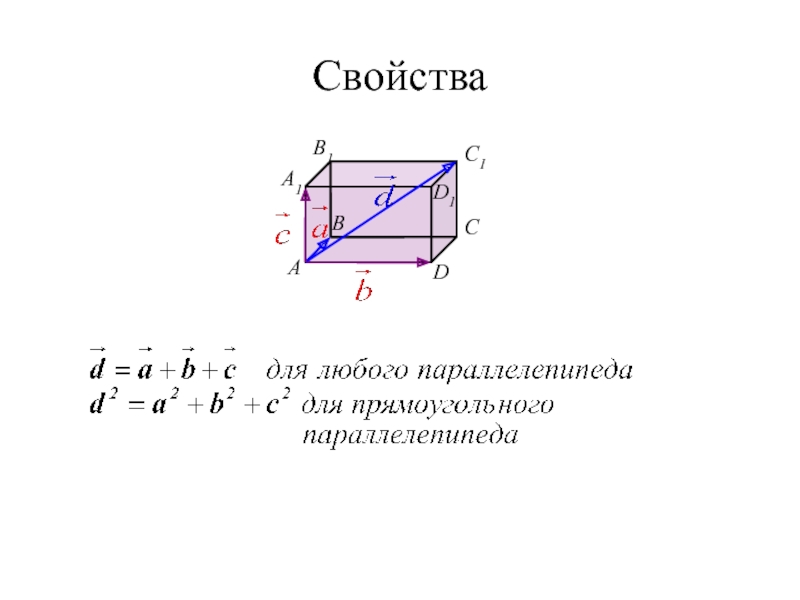
- 16. Свойства B А C D A1 B1 C1 D1
- 17. Вычитание Разностью векторов и
- 18. Вычитание B A Правило трех точек C
- 19. Умножение вектора на число
- 20. Свойства
- 21. Определение компланарных векторов Компланарные векторы –
- 22. О компланарных векторах Любые два вектора
- 23. Признак компланарности
- 24. Разложение вектора По двум неколлинеарным векторам По трем некомпланарным векторам
- 25. Разложение вектора по двум неколлинеарным векторам Теорема.
- 26. Разложение вектора по трем некомпланарным векторам Если
- 27. Доказательство теоремы С O A B P1 P2 P
- 28. Скалярное произведение векторов Скалярным произведением двух
- 29. Следствие 1. Косинус угла между векторами
- 30. Базисные задачи
- 31. Вектор, проведенный в середину отрезка, Доказательство равен
- 32. Доказательство С A B O
- 33. Вектор, соединяющий середины двух отрезков, С A
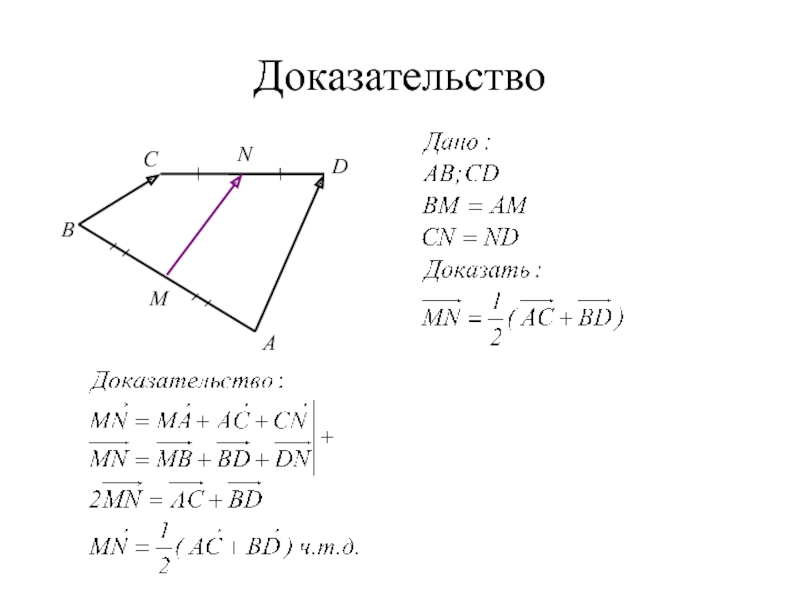
- 34. Доказательство С A B D M N
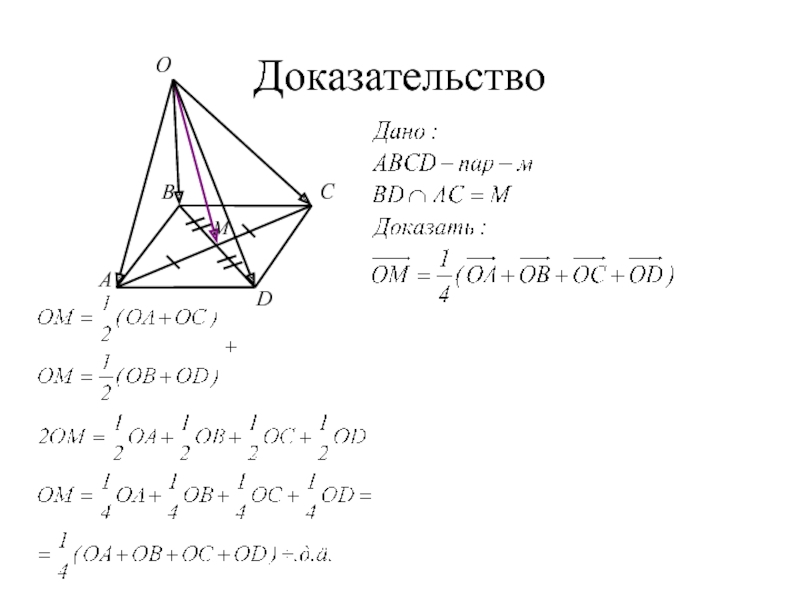
- 35. Вектор, проведенный в точку пересечения диагоналей параллелограмма,
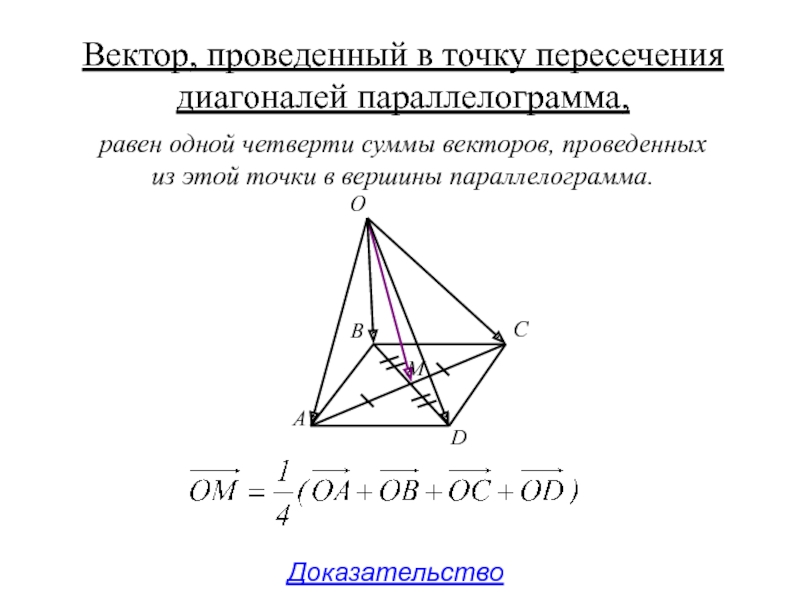
- 36. Доказательство A B C D O M
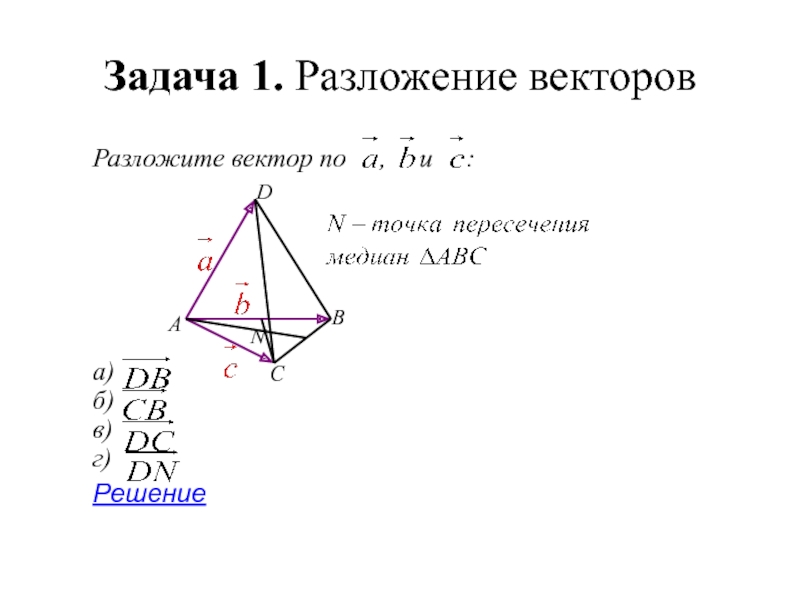
- 37. Задача 1. Разложение векторов Разложите вектор по
- 38. Решение а) б) в) г)
- 39. Задача 2. Сложение и вычитание Упростите выражения: а) б) в) г) д) е) Решение
- 40. Решение а) б) в) г) д) е)
Понятие вектора в пространстве Вектор(направленный отрезок) – отрезок, для которого указано какой из его концов считается началом, а какой – концом. Длина вектора
Слайд 2Понятие вектора в пространстве
Вектор(направленный отрезок) –
отрезок, для которого указано какой
из его концов считается началом, а какой – концом.
Длина вектора – длина отрезка AB.
Длина вектора – длина отрезка AB.
А
В
M
Слайд 3
Нулевым вектором называется вектор, начало и конец которого совпадают.
Единичным вектором называется
вектор, длина которого равна единице.
Векторы называются коллинеарными, если они лежат на одной прямой или параллельных прямых.
Векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Векторы называются коллинеарными, если они лежат на одной прямой или параллельных прямых.
Векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Слайд 4Коллинеарные векторы
Среди коллинеарных различают:
Сонаправленные векторы
Противоположно направленные векторы
Слайд 5Равные векторы
Равные векторы - сонаправленные векторы,
длины которых равны.
От любой точки
можно отложить вектор,
равный данному, и притом только один.
равный данному, и притом только один.
Слайд 6Противоположные векторы
Противоположные векторы – противоположно направленные векторы, длины которых равны.
Вектором, противоположным
нулевому,
считается нулевой вектор.
считается нулевой вектор.
Слайд 9Сложение векторов
Правило треугольника
Правило параллелограмма
Правило многоугольника
Правило параллелепипеда
Слайд 13Правило многоугольника
Сумма векторов равна вектору, проведенному
из начала первого в конец последнего(при
последовательном откладывании).
B
A
C
D
E
Пример
Слайд 15
Правило параллелепипеда
B
А
C
D
A1
B1
C1
D1
Вектор, лежащий на диагонали параллелепипеда, равен сумме векторов, проведенных из
той же точки и лежащих на трех измерениях параллелепипеда.
Слайд 17Вычитание
Разностью векторов и называется такой
вектор, сумма которого
с вектором равна
вектору .
вектору .
Слайд 21
Определение компланарных векторов
Компланарные векторы – векторы, при откладывании которых от одной
и той же точки пространства, они будут лежать в одной плоскости.
Пример:
Пример:
B
А
C
D
A1
B1
C1
D1
Слайд 22
О компланарных векторах
Любые два вектора всегда компланарны.
Три вектора, среди которых имеются
два коллинеарных, компланарны.
α
если
Слайд 25Разложение вектора по двум неколлинеарным векторам
Теорема.
Любой вектор можно разложить по
двум
данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом.
данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом.
Слайд 26Разложение вектора по трем некомпланарным векторам
Если вектор p представлен в виде
где
x, y, z – некоторые числа, то говорят, что вектор
разложен по векторам , и .
Числа x, y, z называются коэффициентами разложения.
Теорема
Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.
разложен по векторам , и .
Числа x, y, z называются коэффициентами разложения.
Теорема
Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.
Слайд 28Скалярное произведение векторов
Скалярным произведением двух векторов называется число
Замечание. Если два вектора
являются перпендикулярными, то их скалярное произведение равно нулю, и наоборот.
Теорема. Скалярное произведение двух векторов
вычисляется по формуле
Теорема. Скалярное произведение двух векторов
вычисляется по формуле
Слайд 29Следствие 1. Косинус угла между векторами
вычисляется по формуле
Следствие 2. Необходимое и
достаточное условие перпендикулярности двух векторов выражается равенством
Слайд 31Вектор, проведенный в середину отрезка,
Доказательство
равен полусумме векторов, проведенных из той же
точки в его концы.
Слайд 33Вектор, соединяющий середины двух отрезков,
С
A
B
D
M
N
С
A
B
D
M
N
Доказательство
равен полусумме векторов, соединяющих их концы.
Слайд 35Вектор, проведенный в точку пересечения диагоналей параллелограмма,
A
B
C
D
O
M
Доказательство
равен одной четверти суммы векторов,
проведенных из этой точки в вершины параллелограмма.
