деятельность как способ формирования метапредметных результатов обучения в условиях реализации ФГОС»
Гуровой Ирины Ивановны
МБОУ «Краснослободский многопрофильный лицей» Краснослободского муниципального района РМ
на тему:
Методическая разработка урока геометрии в 7 классе с элементами исследования
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Аттестационная работа. Методическая разработка урока геометрии в 7 классе с элементами исследования презентация
Содержание
- 1. Аттестационная работа. Методическая разработка урока геометрии в 7 классе с элементами исследования
- 2. Теорема о сумме углов треугольника урок геометрии в 7 классе
- 3. Цели урока: изучить теорему о сумме углов
- 4. План урока: Организационный момент. Фронтальный опрос. Практическая
- 5. Ответьте на вопросы: Дайте определение треугольника. Назовите
- 6. Задание: Постройте у себя в тетрадях несколько
- 7. Вопрос: Где еще на сегодняшнем уроке нам
- 8. Историческая справка Сумма углов треугольника была практическим
- 9. А В С 1 2 3
- 10. Устная работа: Найдите градусную меру угла С.
- 11. Решение задач: Задача 1. Пусть треугольник АВС
- 12. Решение задач: Задача 3. На каком из
- 13. Решение задач: Задача 4. Чему равна сумма
- 14. Подведение итогов: Какой ты треугольник ни возьмешь,
Теорема о сумме углов треугольника урок геометрии в 7 классе
Слайд 1Аттестационная работа
слушателя курсов повышения квалификации по программе: «Проектная и исследовательская
Слайд 3Цели урока:
изучить теорему о сумме углов треугольника;
научить учащихся применять ее при
решении задач;
формировать умение анализировать, обобщать, использовать элементы исследования;
развивать внимание, мышление, математическую речь.
формировать умение анализировать, обобщать, использовать элементы исследования;
развивать внимание, мышление, математическую речь.
Слайд 4План урока:
Организационный момент.
Фронтальный опрос.
Практическая работа с элементами исследования.
Изучение теоремы о сумме
углов треугольника.
Психологическая разгрузка
(физкультурная пауза).
Закрепление изученного материала
(устная работа, решение задач, ).
Подведение итогов.
Задание на дом.
Психологическая разгрузка
(физкультурная пауза).
Закрепление изученного материала
(устная работа, решение задач, ).
Подведение итогов.
Задание на дом.
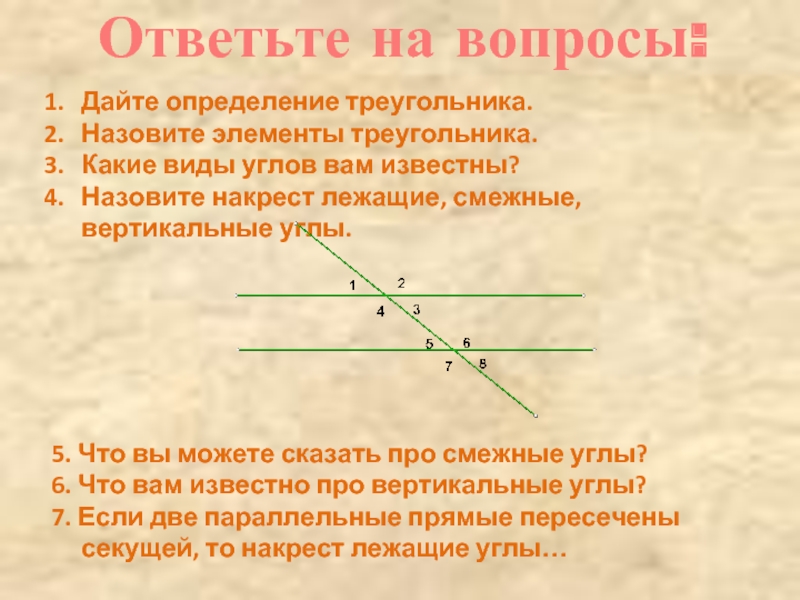
Слайд 5Ответьте на вопросы:
Дайте определение треугольника.
Назовите элементы треугольника.
Какие виды углов вам известны?
Назовите
накрест лежащие, смежные, вертикальные углы.
5. Что вы можете сказать про смежные углы?
6. Что вам известно про вертикальные углы?
7. Если две параллельные прямые пересечены секущей, то накрест лежащие углы…
5. Что вы можете сказать про смежные углы?
6. Что вам известно про вертикальные углы?
7. Если две параллельные прямые пересечены секущей, то накрест лежащие углы…
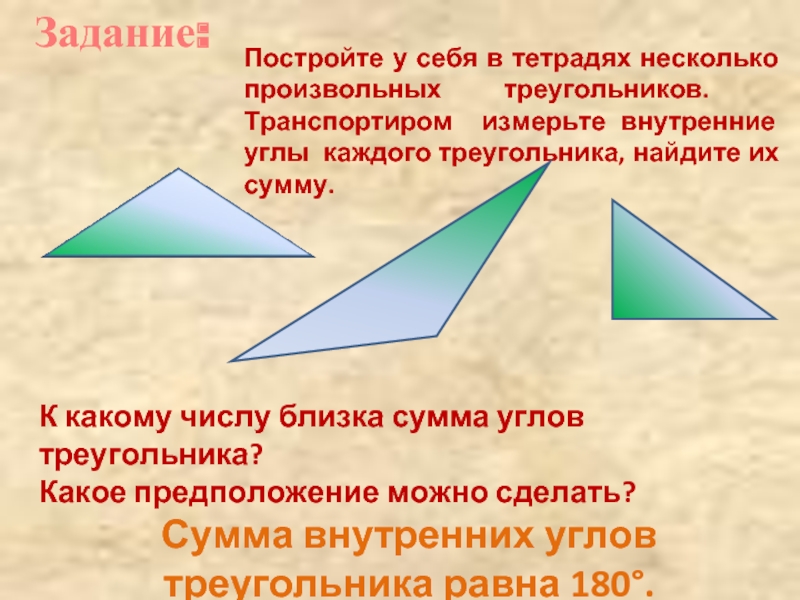
Слайд 6Задание:
Постройте у себя в тетрадях несколько произвольных треугольников. Транспортиром измерьте внутренние
углы каждого треугольника, найдите их сумму.
К какому числу близка сумма углов треугольника?
Какое предположение можно сделать?
Сумма внутренних углов треугольника равна 180°.
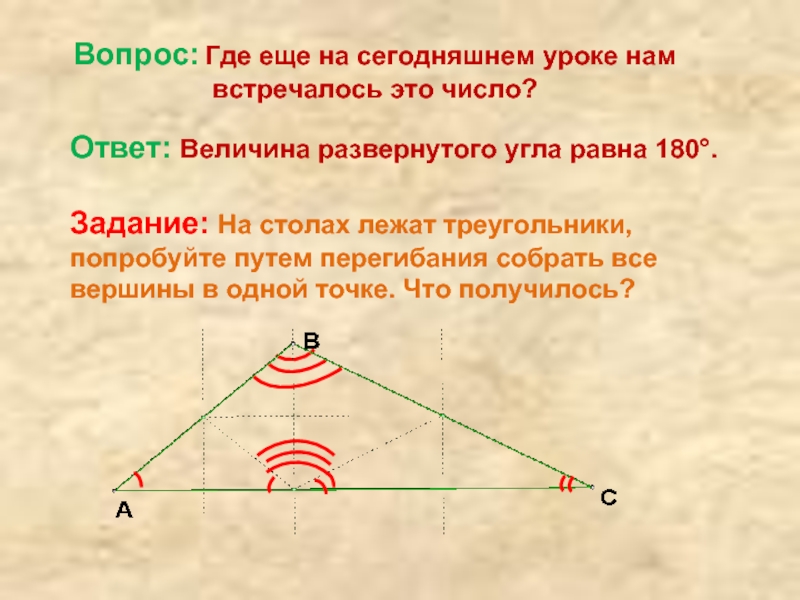
Слайд 7Вопрос: Где еще на сегодняшнем уроке нам встречалось это число?
Ответ: Величина развернутого угла равна 180°.
Задание: На столах лежат треугольники, попробуйте путем перегибания собрать все вершины в одной точке. Что получилось?
Слайд 8Историческая справка
Сумма углов треугольника была практическим путем установлена еще в Древнем
Египте. Прокл утверждал, что доказательство этого факта было известно еще в V веке до нашей эры. Евклид в своей книге «Начала» тоже приводит доказательство этой теоремы.
Слайд 9
А
В
С
1
2
3
4
5
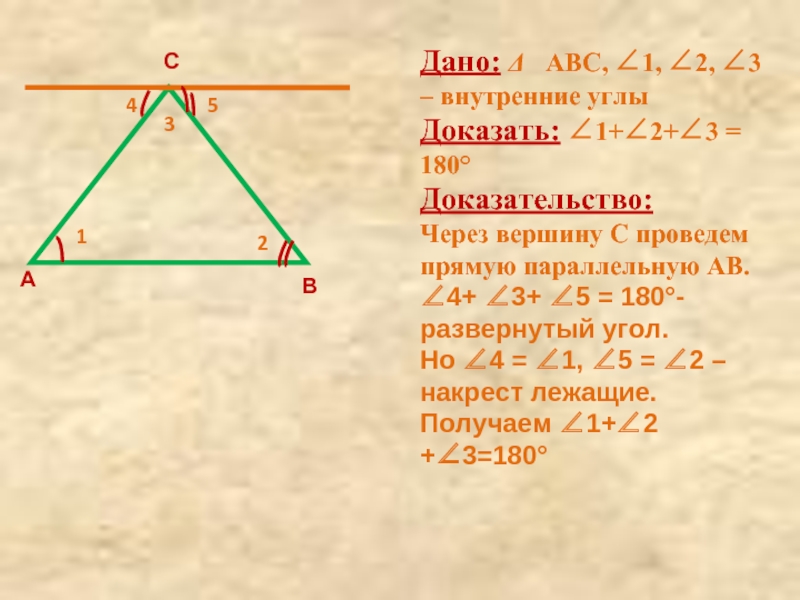
Дано: Δ АВС, ∠1, ∠2, ∠3 – внутренние углы
Доказать: ∠1+∠2+∠3
= 180°
Доказательство:
Через вершину С проведем прямую параллельную АВ.
∠4+ ∠3+ ∠5 = 180°- развернутый угол.
Но ∠4 = ∠1, ∠5 = ∠2 – накрест лежащие.
Получаем ∠1+∠2 +∠3=180°
Доказательство:
Через вершину С проведем прямую параллельную АВ.
∠4+ ∠3+ ∠5 = 180°- развернутый угол.
Но ∠4 = ∠1, ∠5 = ∠2 – накрест лежащие.
Получаем ∠1+∠2 +∠3=180°
Слайд 10Устная работа:
Найдите градусную меру угла С.
Какой треугольник изображен на рисунке?
Найдите градусные
меры углов данного треугольника.
Может ли быть в треугольнике два тупых, два прямых, один тупой и один прямой угол?
Любой треугольник имеет хотя бы два острых угла!
Слайд 11Решение задач:
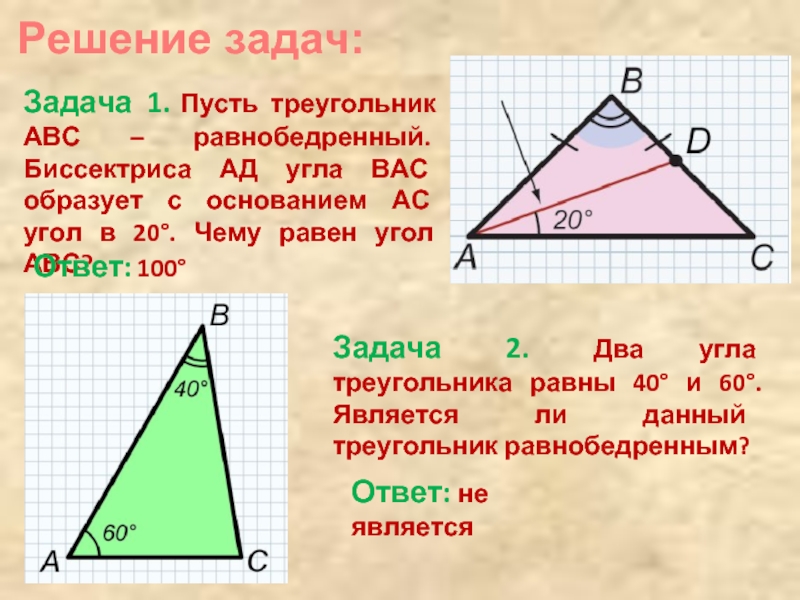
Задача 1. Пусть треугольник АВС – равнобедренный. Биссектриса АД угла
ВАС образует с основанием АС угол в 20°. Чему равен угол АВС?
Ответ: 100°
Задача 2. Два угла треугольника равны 40° и 60°. Является ли данный треугольник равнобедренным?
Ответ: не является
Слайд 12Решение задач:
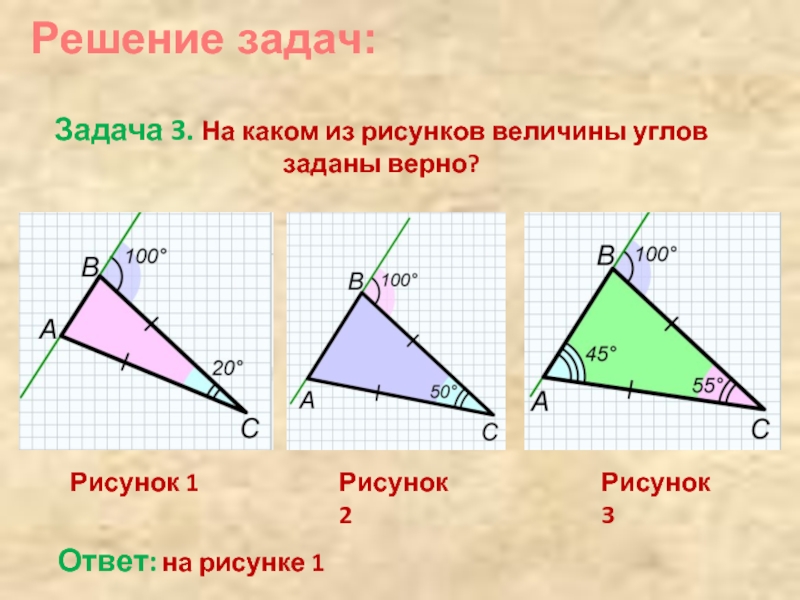
Задача 3. На каком из рисунков величины углов
заданы верно?
Рисунок 1
Рисунок 2
Рисунок 3
Ответ: на рисунке 1
Слайд 13Решение задач:
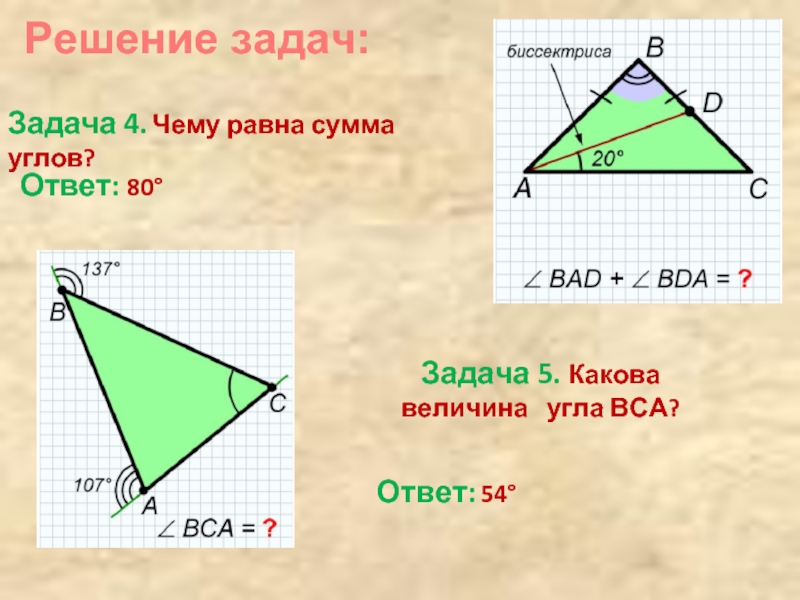
Задача 4. Чему равна сумма углов?
Ответ: 80°
Задача 5. Какова величина
угла ВСА?
Ответ: 54°
Слайд 14Подведение итогов:
Какой ты треугольник ни возьмешь,
В нем сумму всех углов легко
найдешь.
Запомни, что нигде не изменяется она!
И ста восьмидесяти градусам всегда равна!
Запомни, что нигде не изменяется она!
И ста восьмидесяти градусам всегда равна!
Задание на дом:
П. 30, №227(а), №228.
