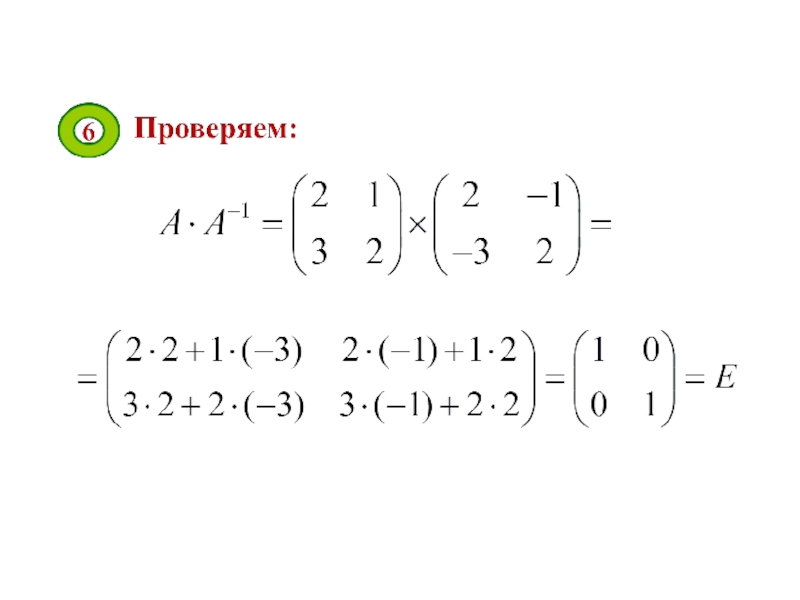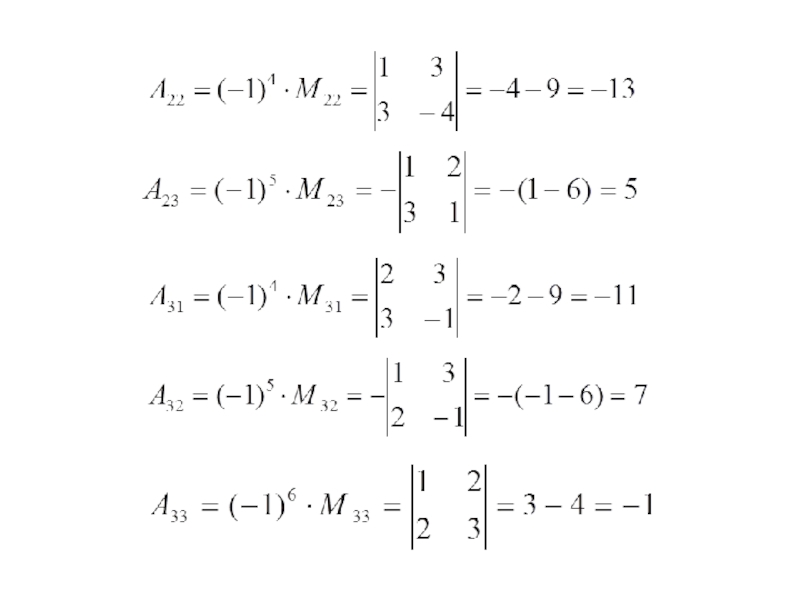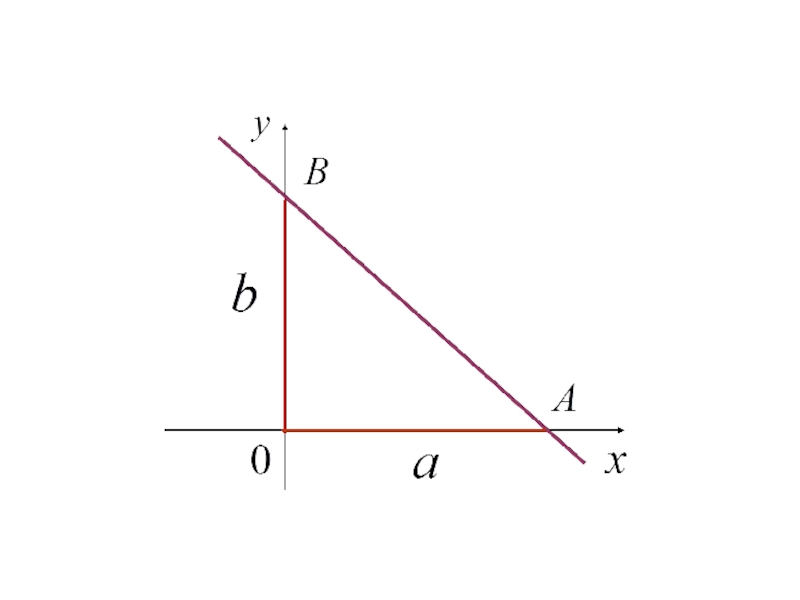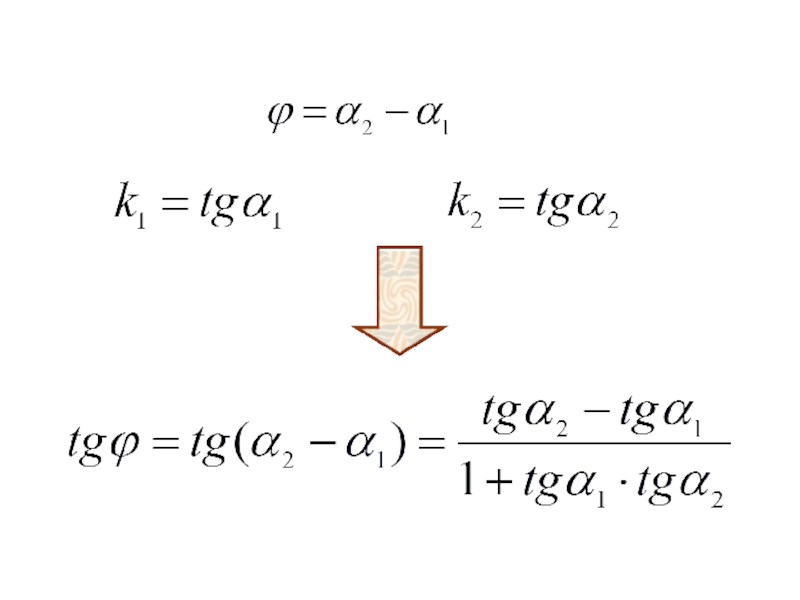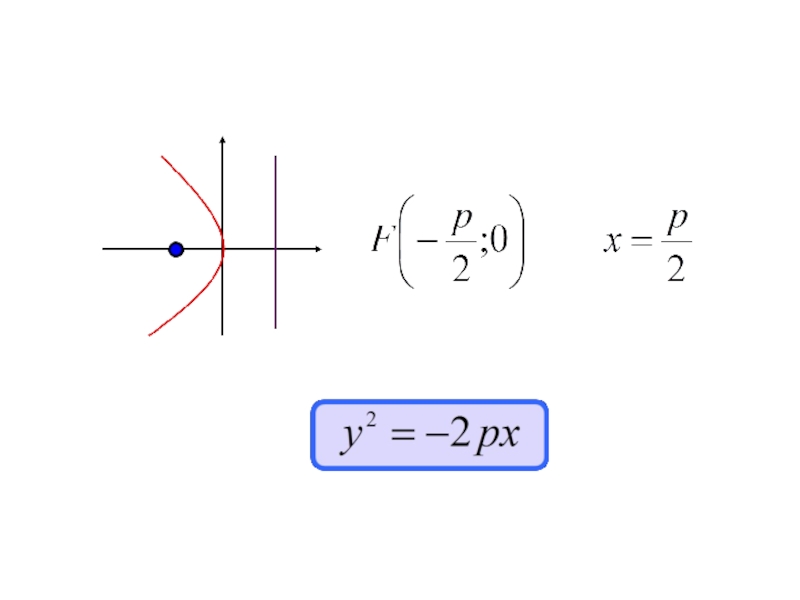- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Высшая математика. Вебинар для студентов заочной формы обучения (дистанционная) презентация
Содержание
- 1. Высшая математика. Вебинар для студентов заочной формы обучения (дистанционная)
- 2. Преподаватель: Кузьмина Ольга Борисовна Кафедра: Информационно-компьютерных технологий KuzminaOB@edu.mubint.ru Сайт: https://mubint.sharepoint.com/kuzmina/
- 3. Порядок изучения дисциплины Форма контроля – экзамен,
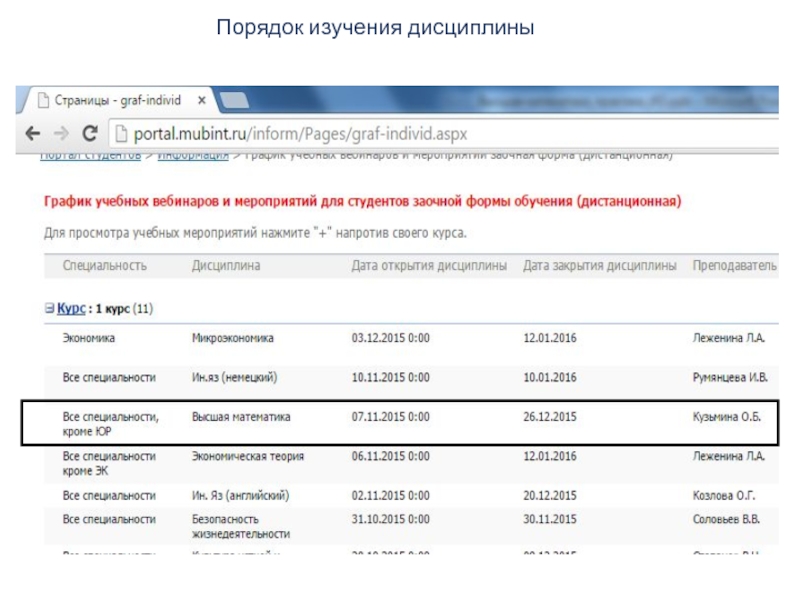
- 4. Порядок изучения дисциплины
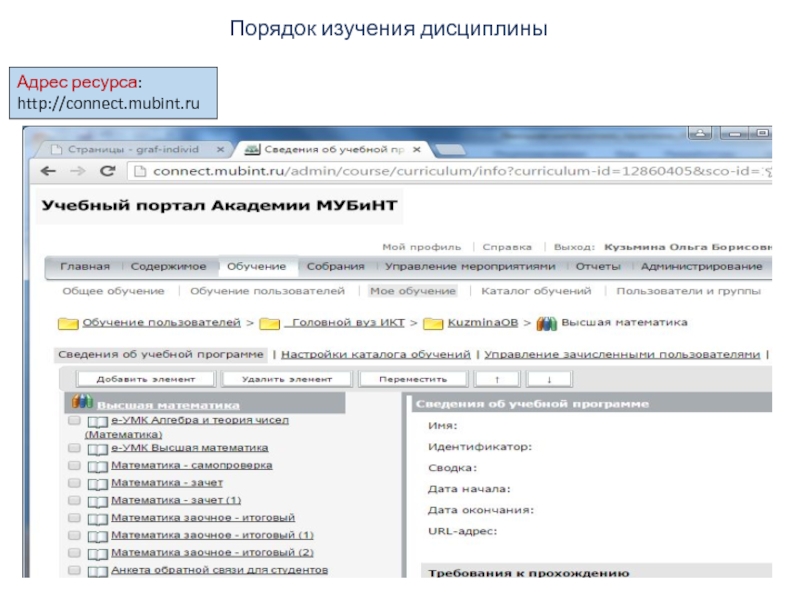
- 5. Порядок изучения дисциплины Адрес ресурса: http://connect.mubint.ru
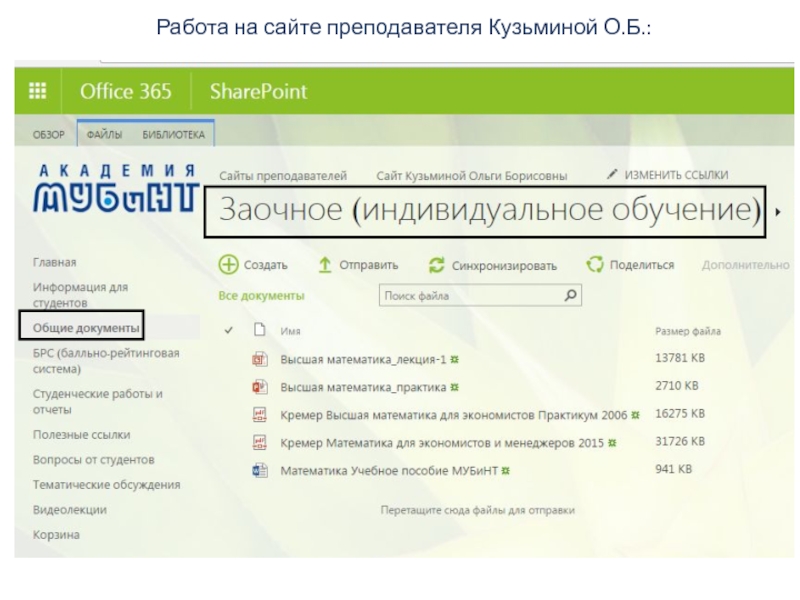
- 6. Работа на сайте преподавателя Кузьминой О.Б.:
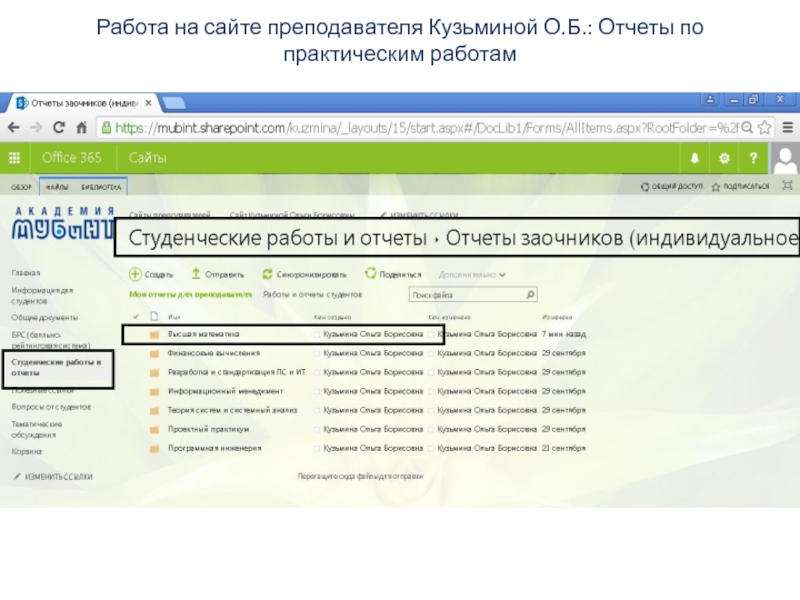
- 7. Работа на сайте преподавателя Кузьминой О.Б.: Отчеты по практическим работам
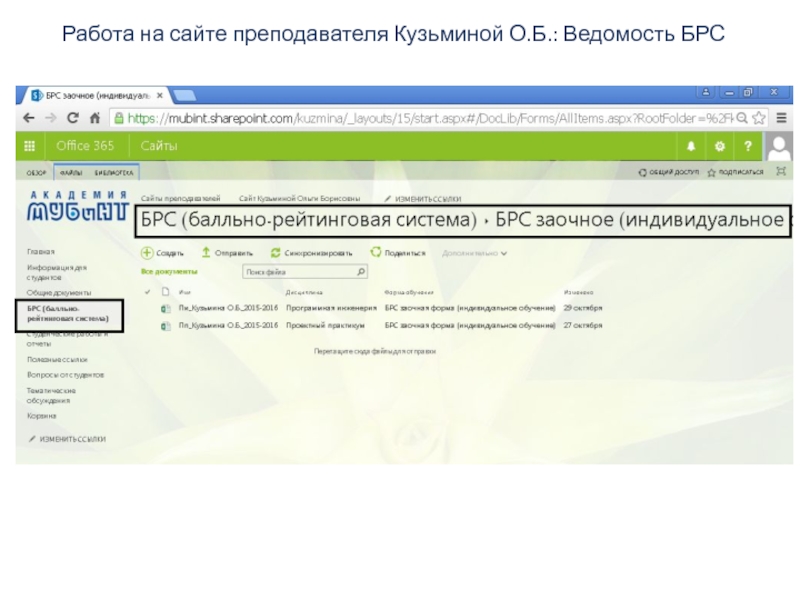
- 8. Работа на сайте преподавателя Кузьминой О.Б.: Ведомость БРС
- 9. Учебно-методические пособия, задания на практические занятия, презентации
- 10. 1. Матрицы и определители
- 11. 1.1. Матрицы и действия над ними Матрицей
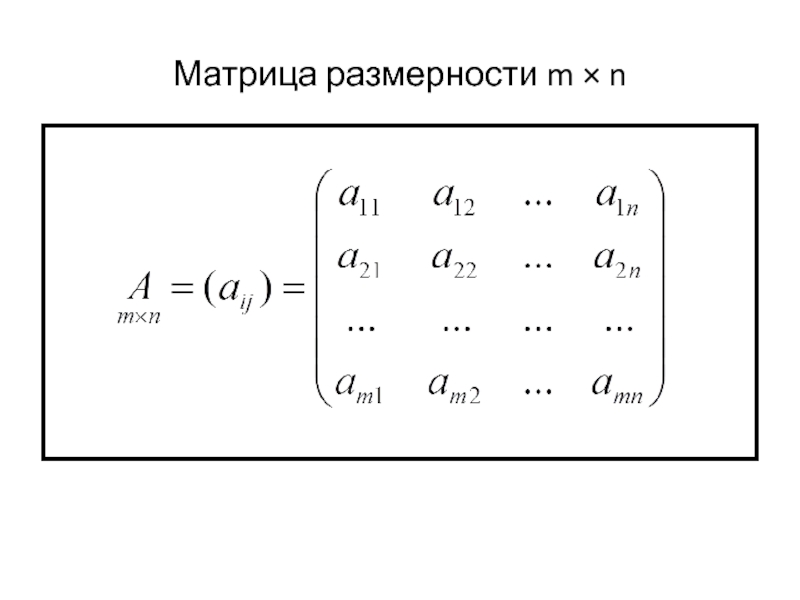
- 13. Матрица размерности m × n
- 15. Пример:
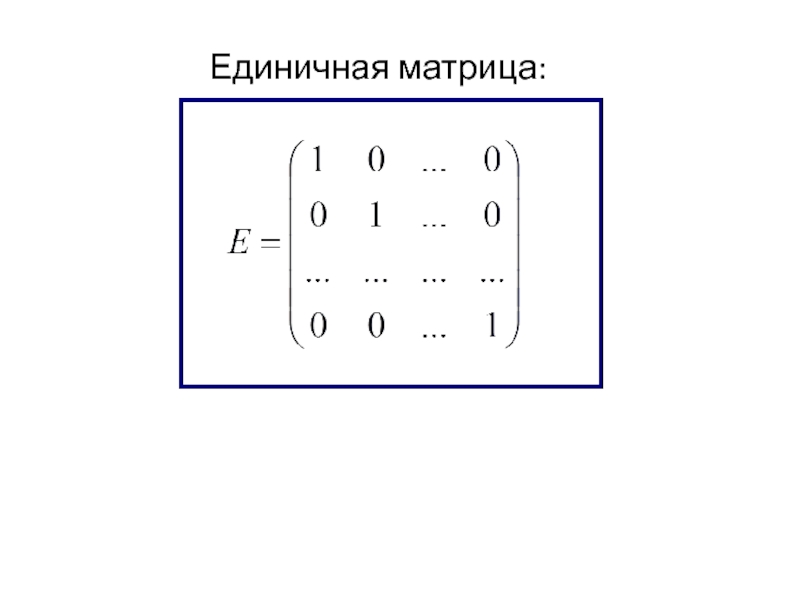
- 17. Единичная матрица:
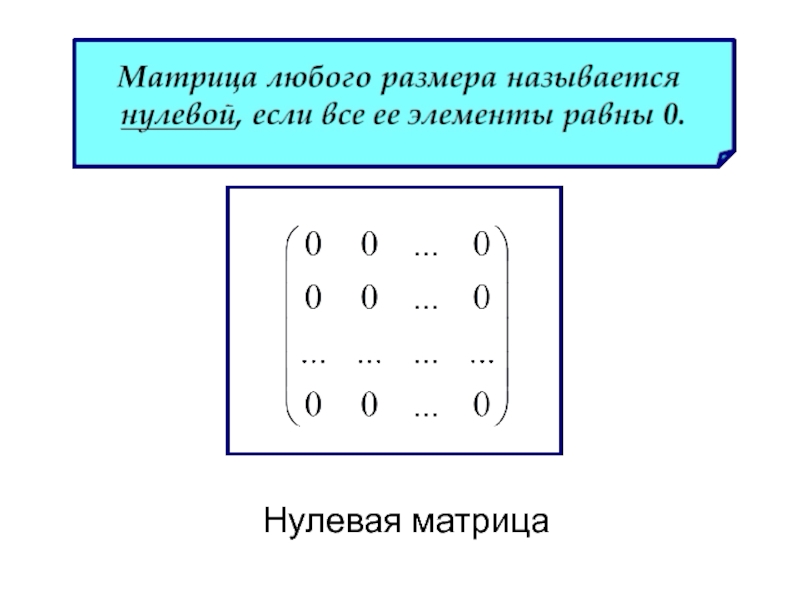
- 18. Нулевая матрица
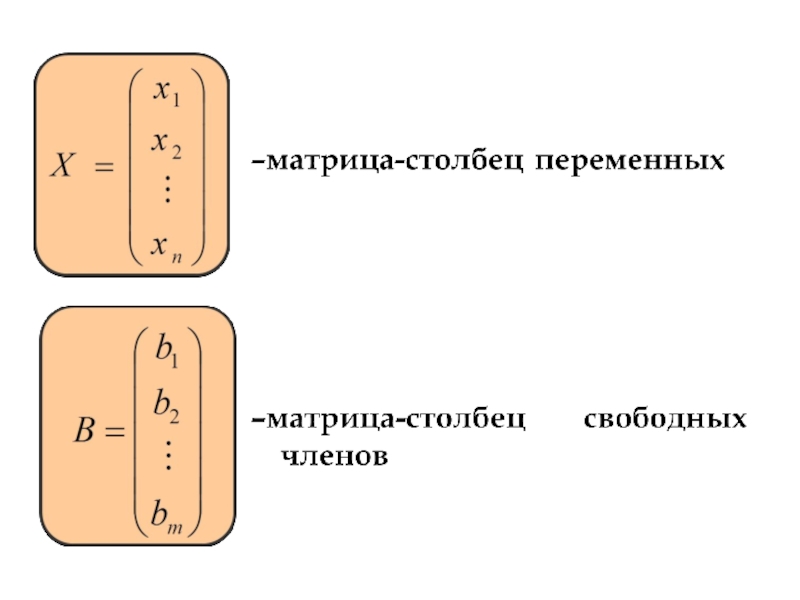
- 19. Матрица-строка
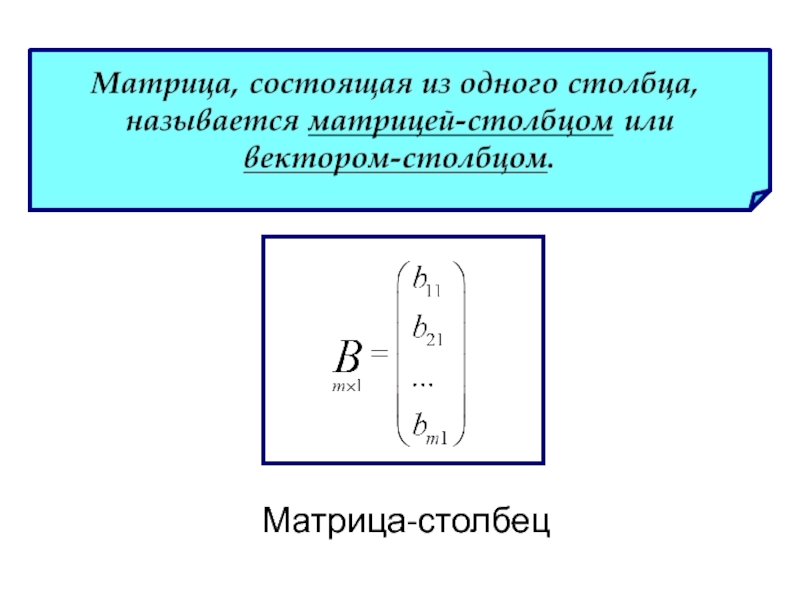
- 20. Матрица-столбец
- 23. 1.2. Действия над матрицами 1.2.1. Умножение матрицы на число
- 26. 1.2.2. Сложение матриц
- 28. Пример: Найти сумму и разность матриц: Решение:
- 29. 1.2.3. Умножение матриц
- 31. Пример: Найти произведение матриц: Решение:
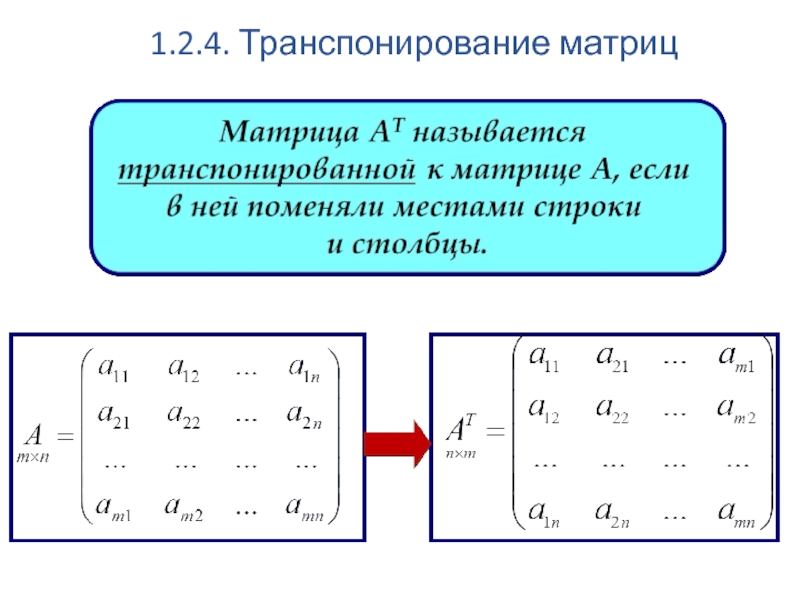
- 33. 1.2.4. Транспонирование матриц
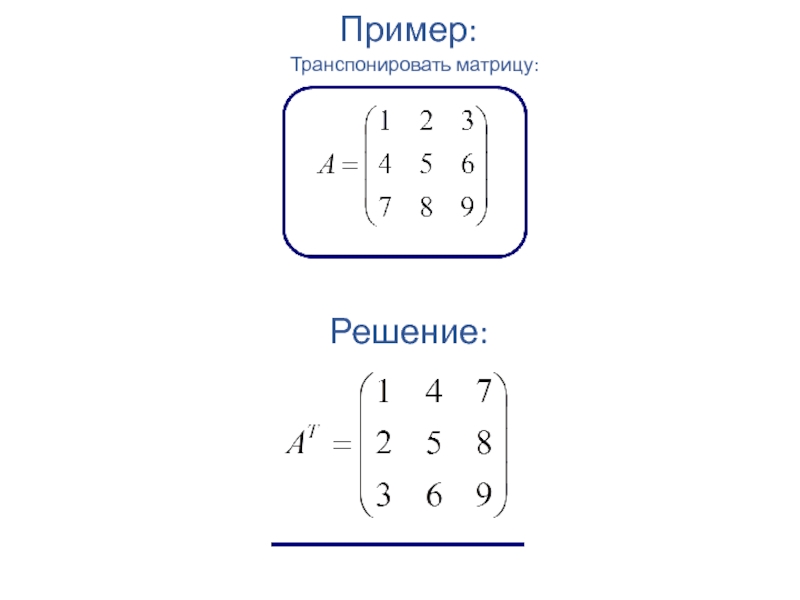
- 34. Пример: Транспонировать матрицу: Решение:
- 35. 1.3. Определитель матрицы
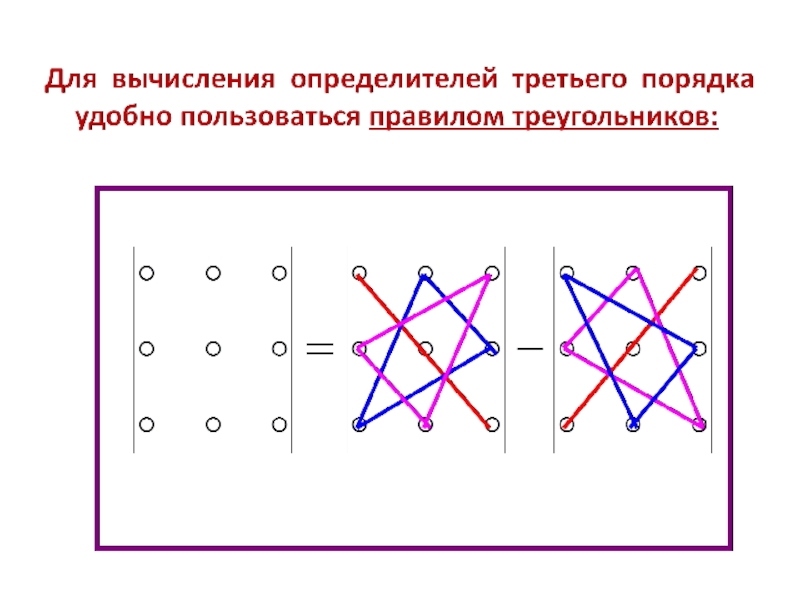
- 40. Пример: Вычислить определители матриц: Решение:
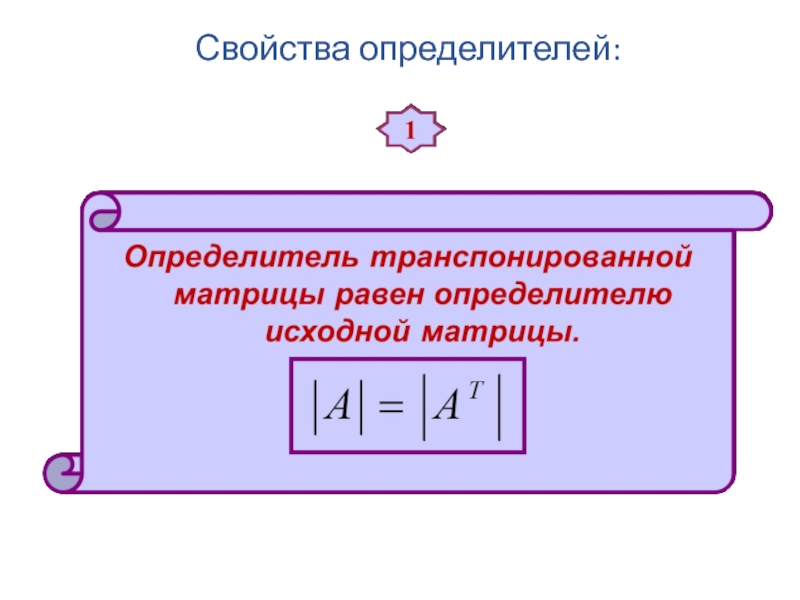
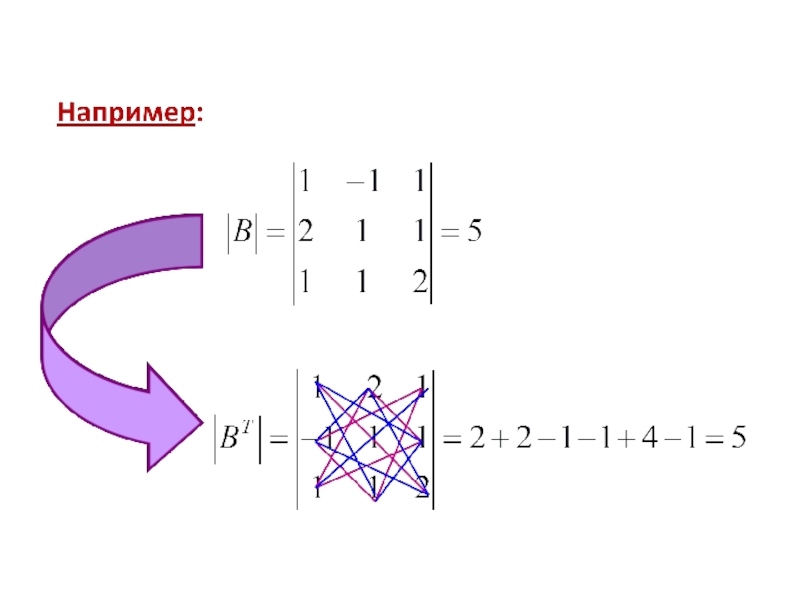
- 44. Свойства определителей:
- 55. Пример: Вычислить определитель:
- 56. Решение:
- 58. 1.4. Обратная матрица
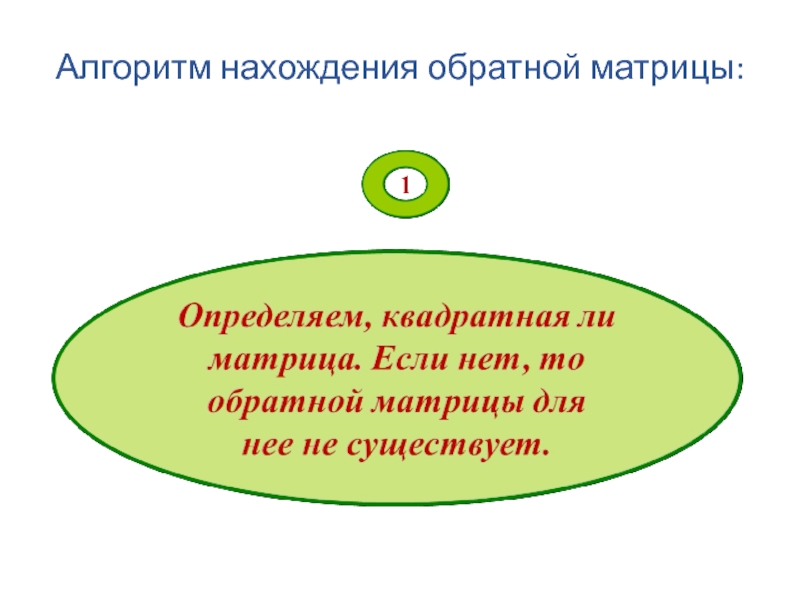
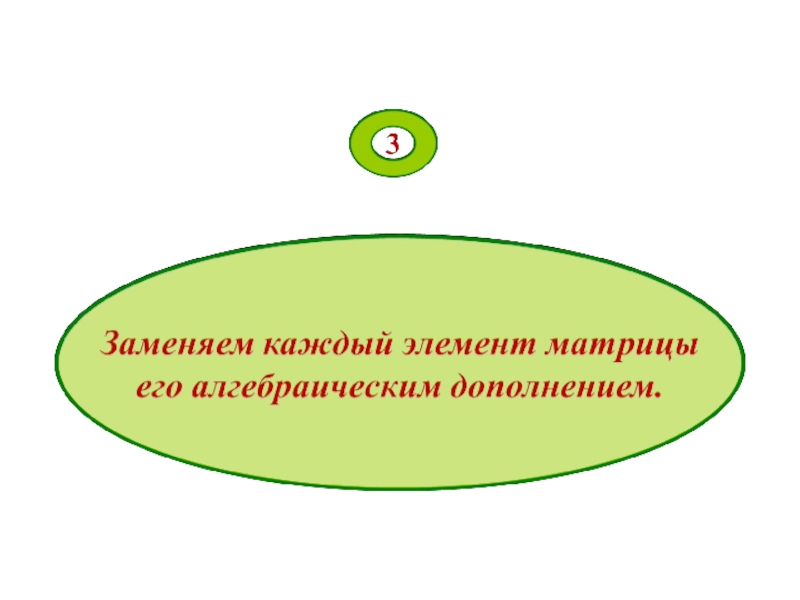
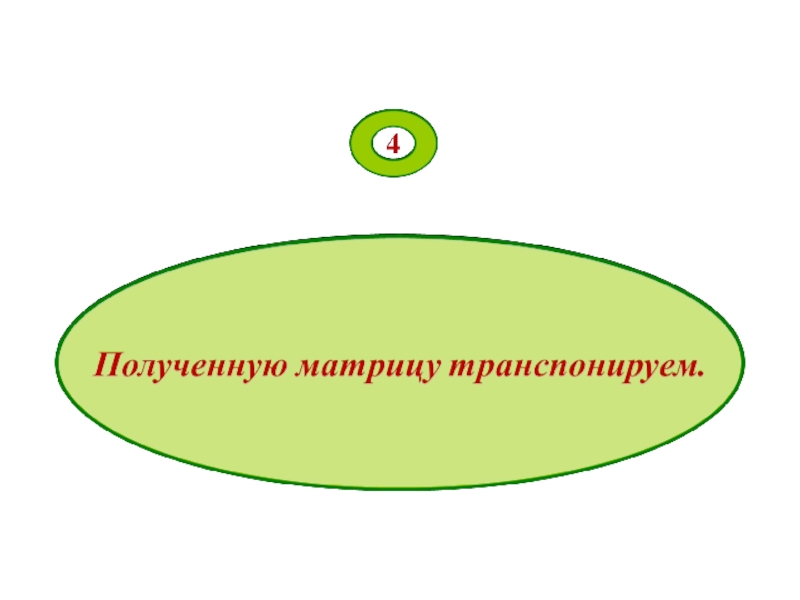
- 59. Алгоритм нахождения обратной матрицы:
- 65. Пример: Найти матрицу, обратную к матрице:
- 66. Решение:
- 70. 2. Системы линейных алгебраических уравнений
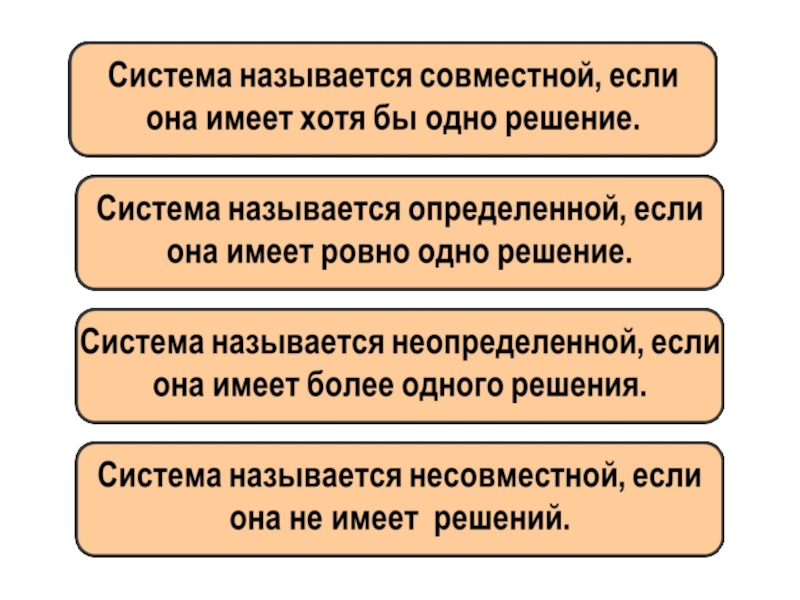
- 71. 2.1. Понятие системы линейных уравнений
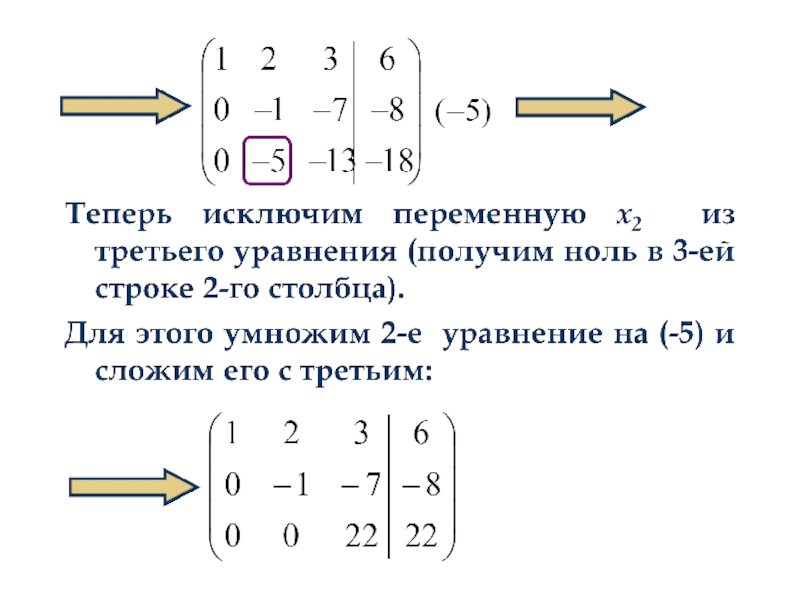
- 78. 2.2. Решение систем линейных уравнений 2.2.1. Метод Гаусса
- 83. 2.2.2. Метод Крамера
- 85. Формулы Крамера
- 90. 2.2.3. Метод обратной матрицы
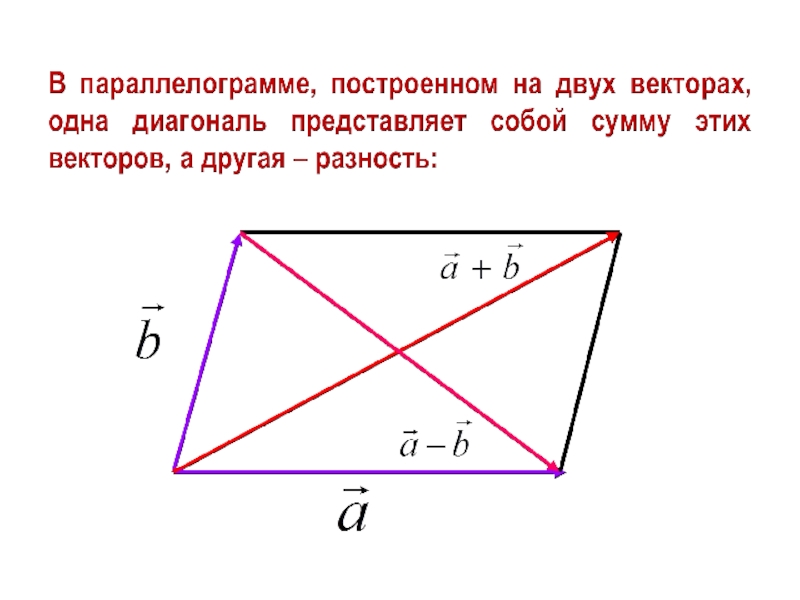
- 97. 3. Векторы и действия над ними
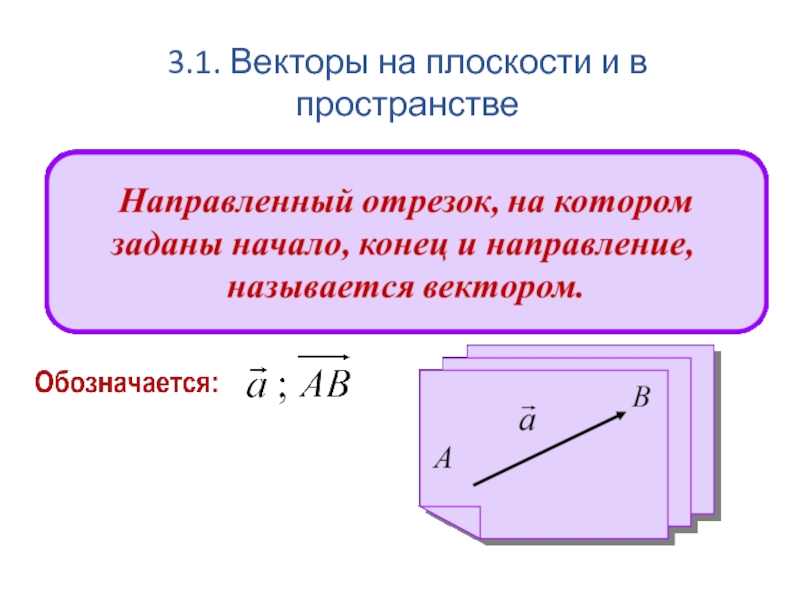
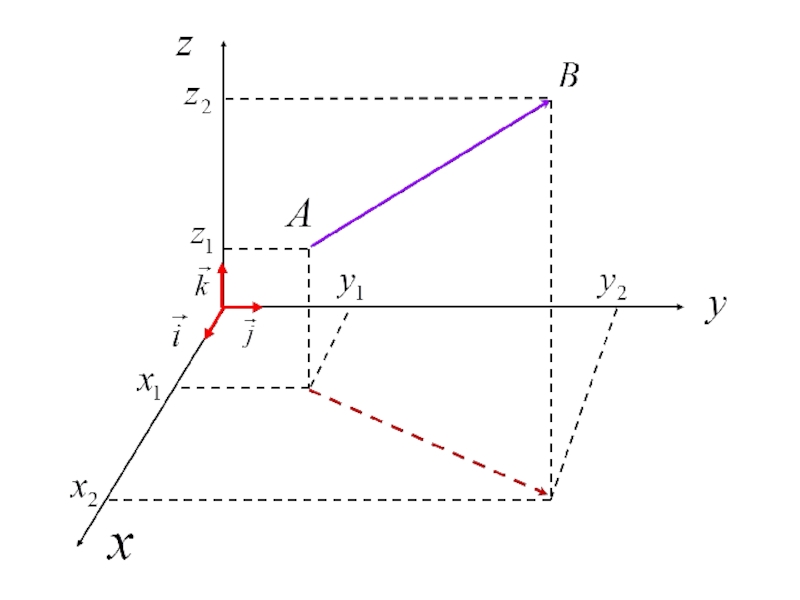
- 98. 3.1. Векторы на плоскости и в пространстве
- 103. Условие коллинеарности векторов
- 112. Условие перпендикулярности векторов
- 113. 4. Уравнение линии
- 114. 4.1. Уравнение прямой на плоскости
- 115. Способы задания прямой на плоскости 1. Уравнение прямой с угловым коэффициентом
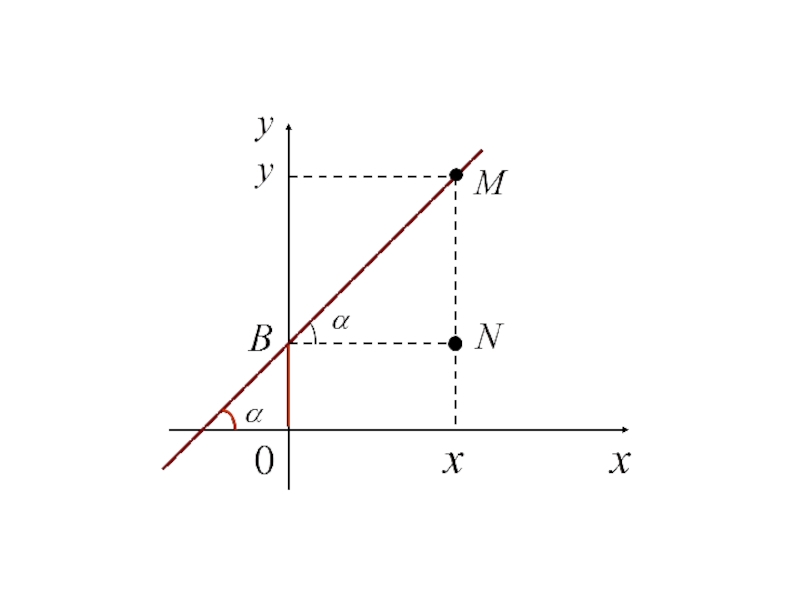
- 117. Уравнение прямой с угловым коэффициентом
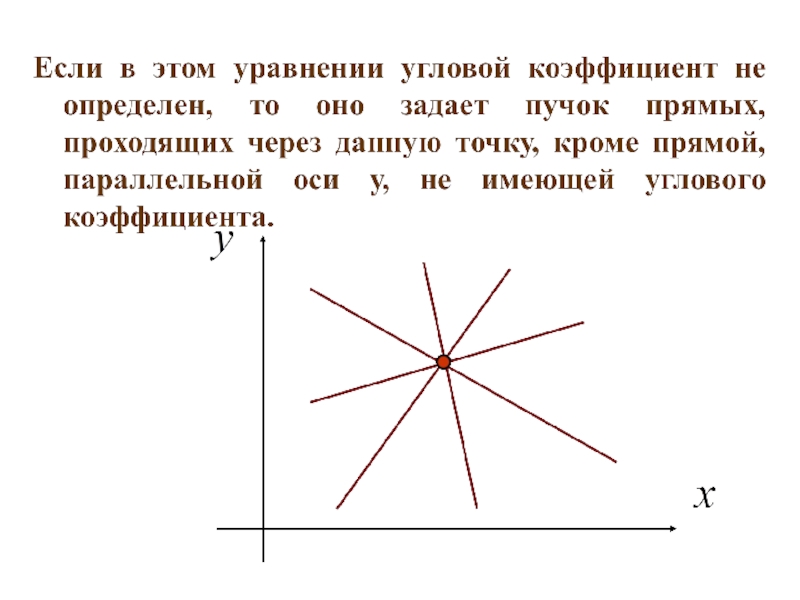
- 120. 2. Уравнение прямой, проходящей через заданную точку в заданном направлении
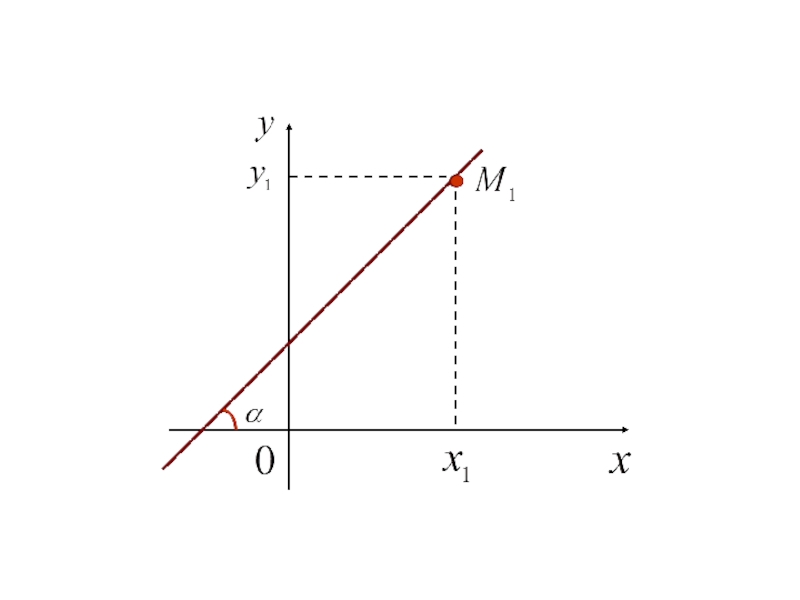
- 122. Уравнение прямой, проходящей через заданную точку в заданном направлении
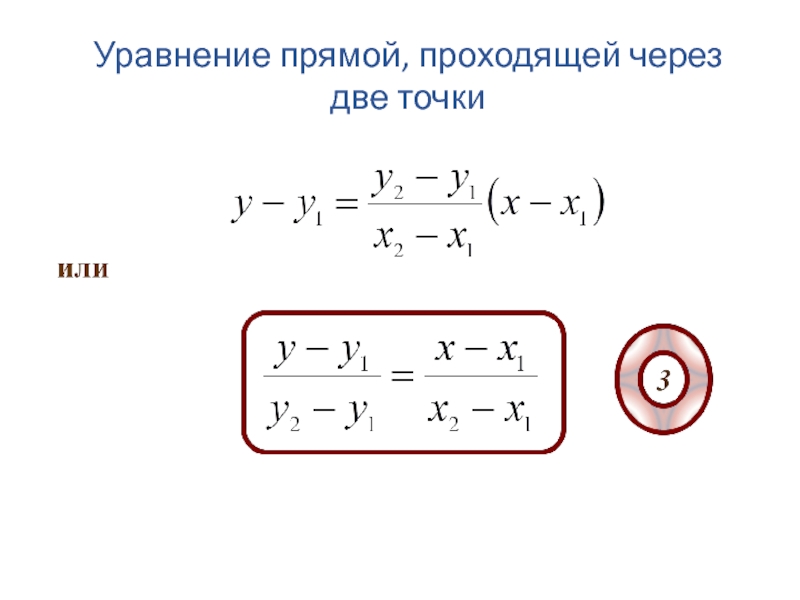
- 124. 3. Уравнение прямой, проходящей через две точки
- 126. Уравнение прямой, проходящей через две точки
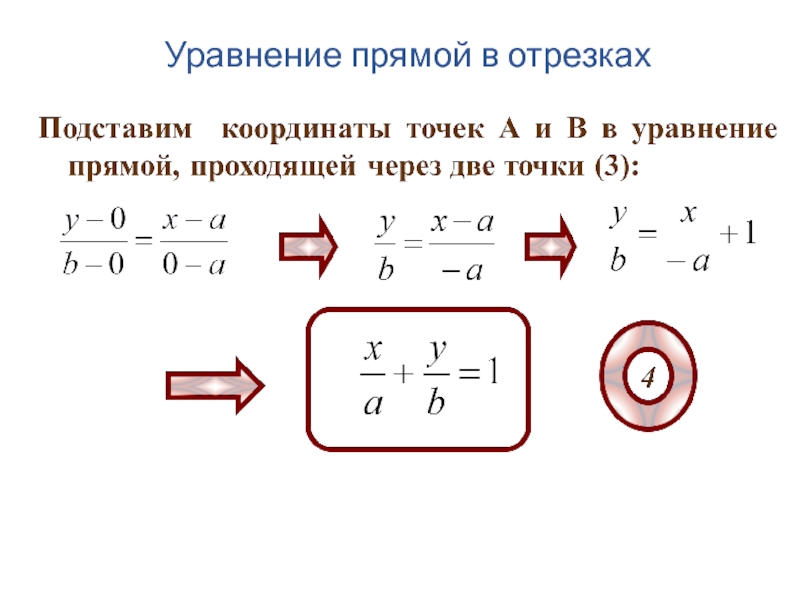
- 129. 4. Уравнение прямой в отрезках
- 131. Уравнение прямой в отрезках
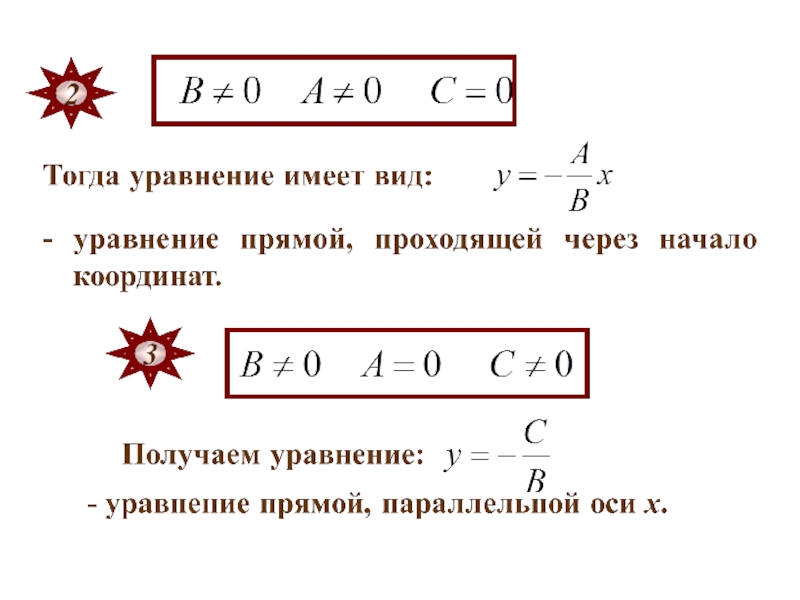
- 134. 5. Общее уравнение прямой
- 138. Общее уравнение прямой
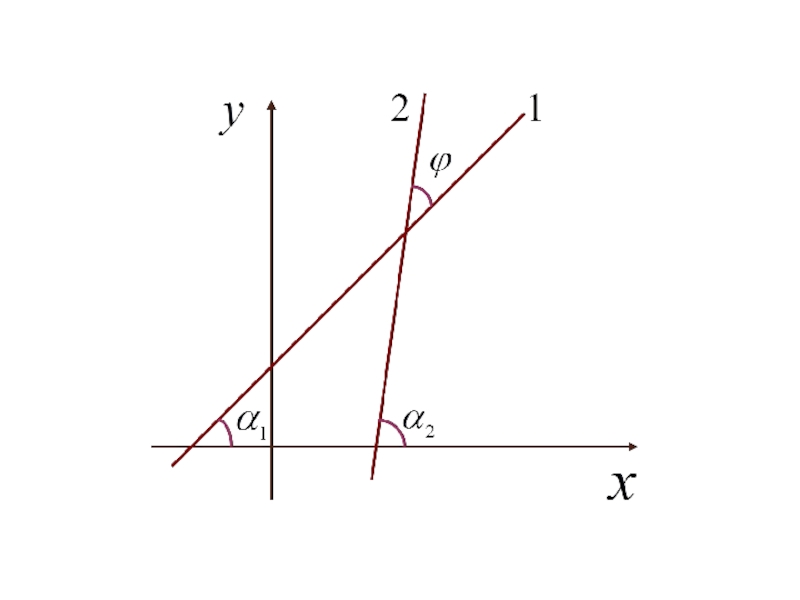
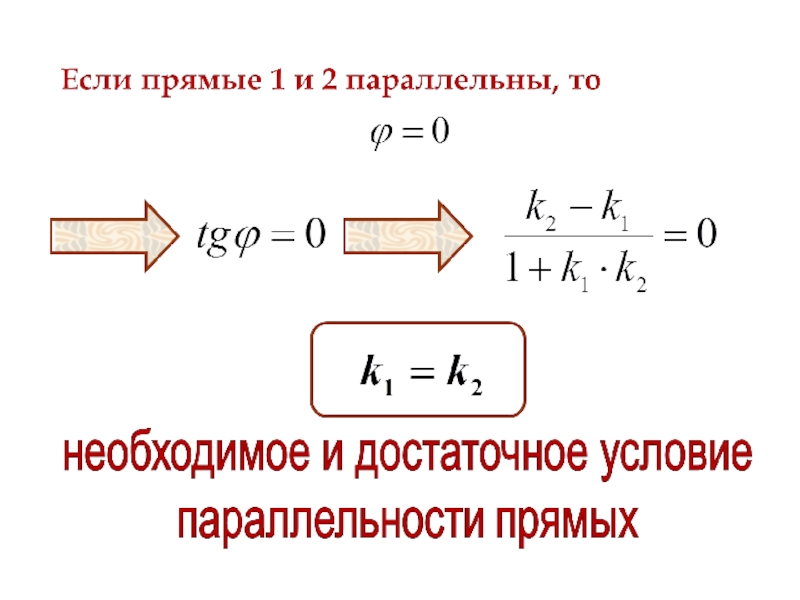
- 139. 4.2. Условия параллельности и перпендикулярности прямых
- 153. 4.3. Окружность и эллипс
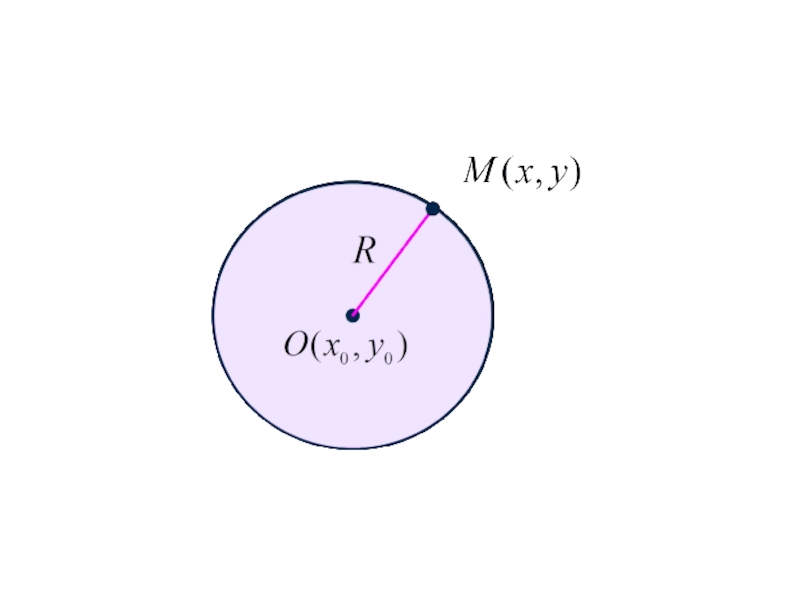
- 155. Нормальное уравнение окружности
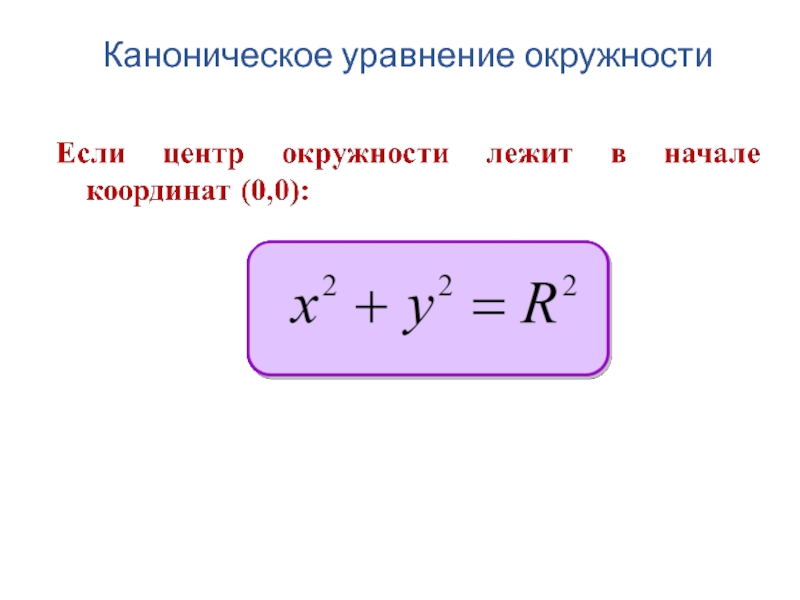
- 156. Каноническое уравнение окружности
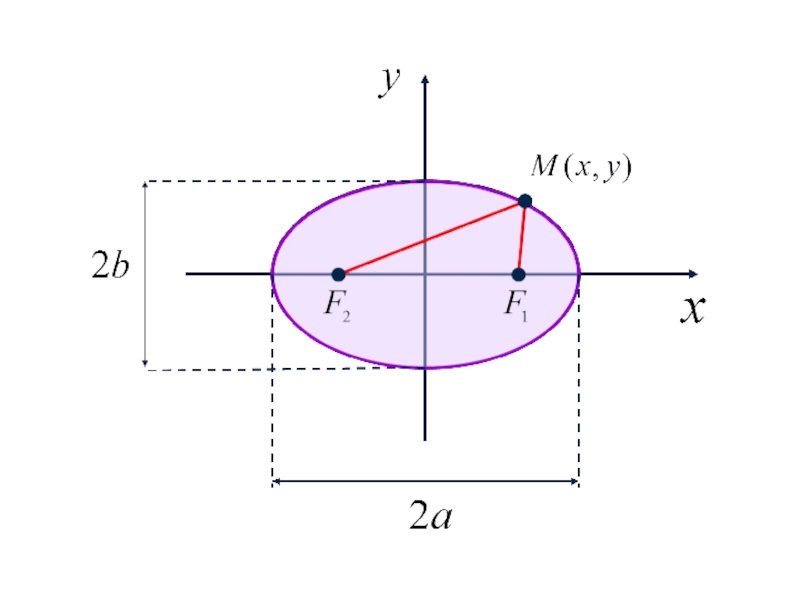
- 160. Каноническое уравнение эллипса
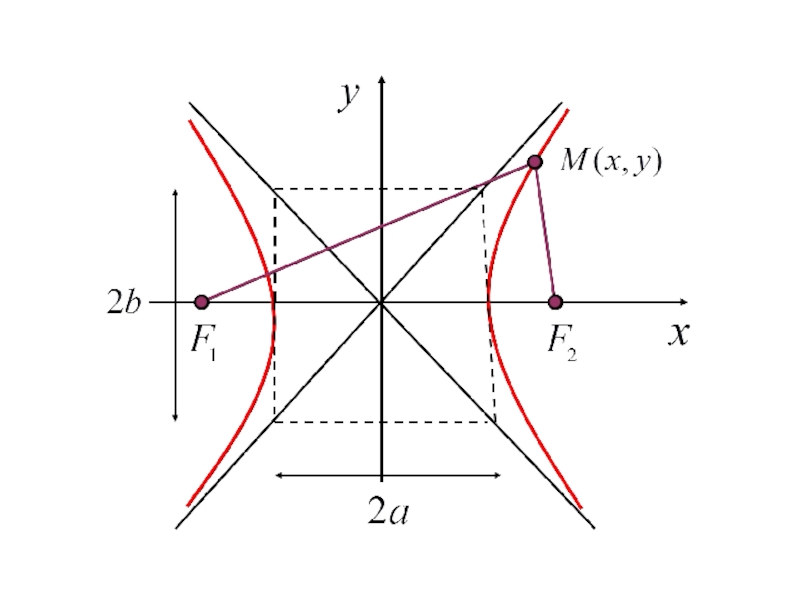
- 163. 4.4. Гипербола
- 167. Каноническое уравнение гиперболы
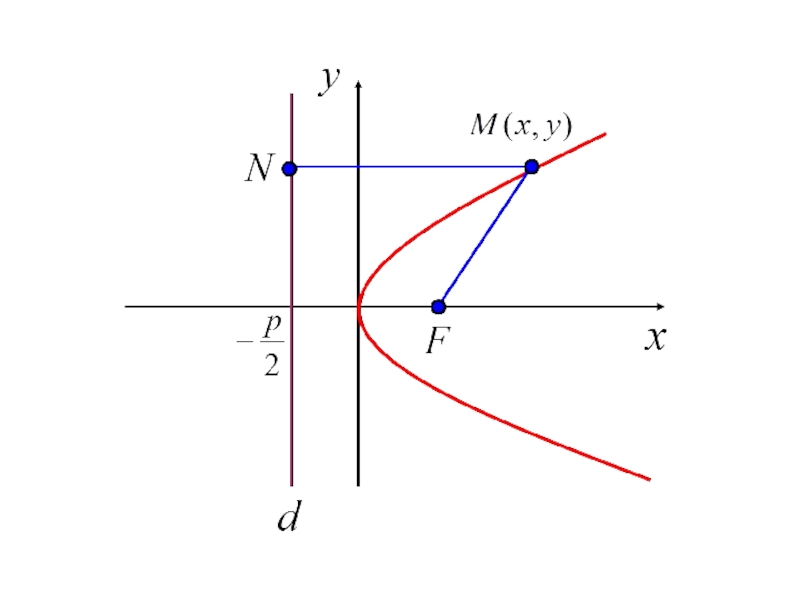
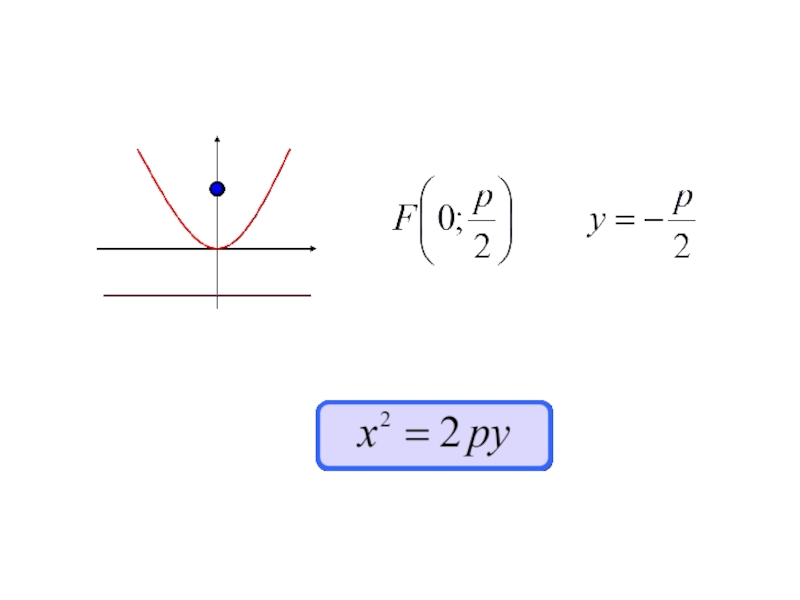
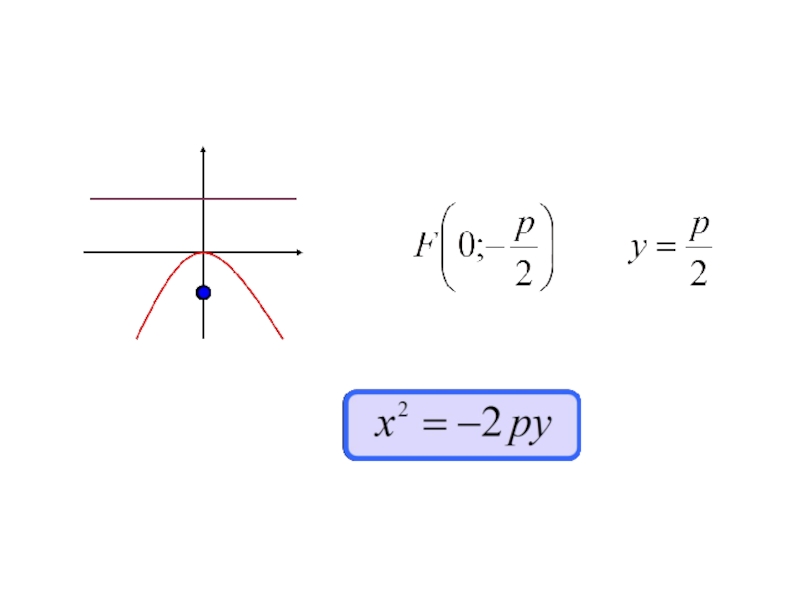
- 170. 4.5. Парабола
- 173. Каноническое уравнение параболы
Преподаватель: Кузьмина Ольга Борисовна Кафедра: Информационно-компьютерных технологий KuzminaOB@edu.mubint.ru Сайт: https://mubint.sharepoint.com/kuzmina/
Слайд 2Преподаватель:
Кузьмина Ольга Борисовна
Кафедра: Информационно-компьютерных технологий
KuzminaOB@edu.mubint.ru
Сайт:
https://mubint.sharepoint.com/kuzmina/
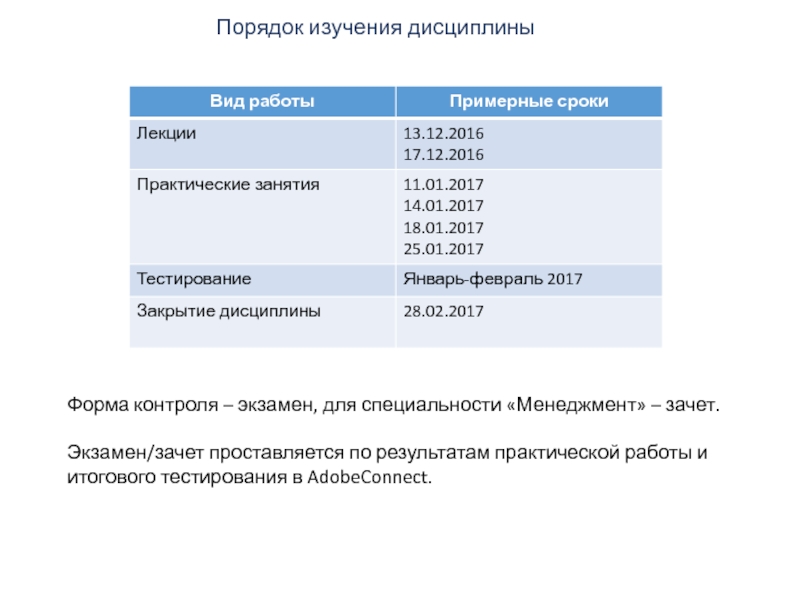
Слайд 3Порядок изучения дисциплины
Форма контроля – экзамен, для специальности «Менеджмент» – зачет.
Экзамен/зачет
проставляется по результатам практической работы и итогового тестирования в AdobeConnect.
Слайд 9Учебно-методические пособия, задания на практические занятия, презентации с лекций-вебинаров и практических
работ выложены на сайте преподавателя Кузьминой О.Б. в разделе «Общие документы: / Заочное (индивидуальное) обучение / Высшая математика».
Литература:
Н.Ш. Кремер Высшая математика для экономистов: учебник для студентов вузов, обучающихся по экономическим специальностям/Н.Ш. Кремер. – М.: ЮНИТИ-ДАНА, 2003-2015 г.г.
Н.Ш. Кремер Высшая математика для экономистов: практикум, 2006 г.
Учебно-методическое пособие «Математика», МУБиНТ
Слайд 111.1. Матрицы и действия над ними
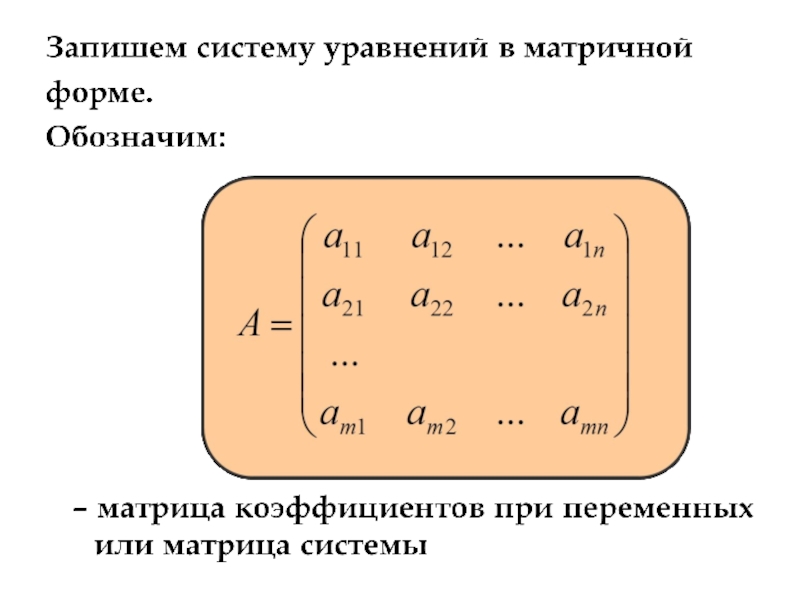
Матрицей размера m × n называется
прямоугольная таблица чисел, содержащая m строк и n столбцов
Числа, составляющие матрицу, называются элементами матрицы
