- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Уравнения и неравенства с модулем презентация
Содержание
- 1. Уравнения и неравенства с модулем
- 2. Уравнение вида | f(x)| = g(x)
- 3. Условие 1 f(х)≥0 (решаем полученное неравенство) Раскрываем
- 4. Условие 2 f(х)
- 5. Решить уравнение |2x+5|=3x-1 1. Условие: 2x+5≥0
- 6. Решить уравнение |2x+5|=3x-1 1. Условие: 2x+5
- 7. Неравенство вида | f(x)| ≥ g(x)
- 8. Решить уравнение |2x+5|>3x-1 1. Условие: 2x+5≥0
- 9. Решить уравнение |2x+5|>3x-1 2. Условие: 2x+53х-1 -2х-3х>-1+5 -5x>4 Х
- 10. Объединим полученные интервалы (-∞;-2,5)и [-2,5;6) Решить
- 11. Уравнение вида | f(x)| =| g(x) |
- 12. |2x+5|=|3x-1| (2x+5)2 =(3x-1)2 (2x+5)2 -(3x-1)2 =0 ((2x+5)-(3x-1))((2x+5)+(3x-1))=0
Слайд 2Уравнение вида | f(x)| = g(x)
Чтобы решить уравнение с модулем
|a|=
a,
условие1 a ≥ 0
-a,
условие2 a<0
Слайд 3Условие 1 f(х)≥0 (решаем полученное неравенство)
Раскрываем модульные скобки с использование условия
3. Решаем полученное уравнение
4. Проверяем соответствие корней условию
Уравнение вида | f(x)| = g(x)
Слайд 4Условие 2 f(х)
3. Решаем полученное уравнение
4. Проверяем соответствие корней условию
Уравнение вида | f(x)| = g(x)
Слайд 5Решить уравнение |2x+5|=3x-1
1. Условие: 2x+5≥0
Раскрываем модульные скобки: по условию выражение под модулем положительно, то модульные скобки просто убираем
2x+5=3x-1
2х-3х=-1-5
-x=-6
X=6 – подходит по условию, следовательно корень
Слайд 6Решить уравнение |2x+5|=3x-1
1. Условие: 2x+5
Раскрываем модульные скобки: по условию выражение под модулем отрицательно, то модульные скобки раскрываем со знаком минус
-(2x+5)=3x-1
-2x-5=3x-1
-2х-3х=-1+5
-5x=4
X=-0,8 – не подходит по условию, следовательно не корень
Ответ: 6
Слайд 7Неравенство вида | f(x)| ≥ g(x)
Решаем аналогично уравнению.
Ставим условие 1
Раскрываем модульные скобки в соответствии с условием
Решаем полученное неравенство
Находим общее решение для условия и решенного неравенства
Ставим условие 2 и выполняем пункты со 2 по 4
Объединяем все полученные промежутки
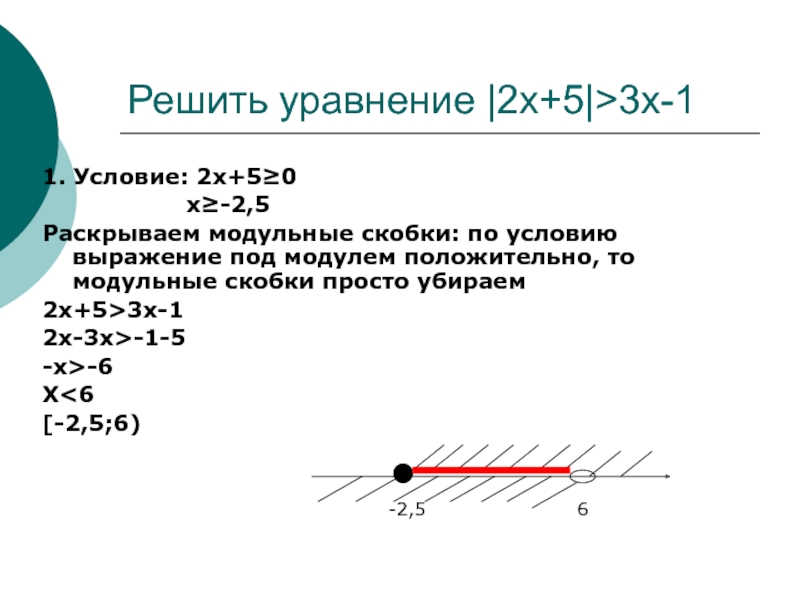
Слайд 8Решить уравнение |2x+5|>3x-1
1. Условие: 2x+5≥0
Раскрываем модульные скобки: по условию выражение под модулем положительно, то модульные скобки просто убираем
2x+5>3x-1
2х-3х>-1-5
-x>-6
X<6
[-2,5;6)
-2,5
6
Слайд 9Решить уравнение |2x+5|>3x-1
2. Условие: 2x+5
Раскрываем модульные скобки: по условию выражение под модулем отрицательно, то модульные скобки раскрываем с минусом
-(2x+5)>3x-1
-2х-5>3х-1
-2х-3х>-1+5
-5x>4
Х<-0,8
-2,5
-0,8
-2,5
(-∞;-2,5)
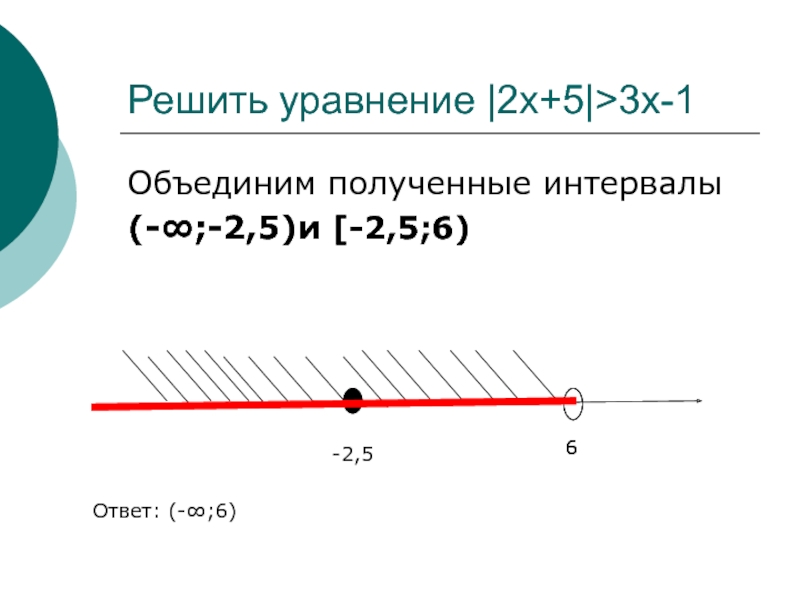
Слайд 10Объединим полученные интервалы
(-∞;-2,5)и [-2,5;6)
Решить уравнение |2x+5|>3x-1
-2,5
6
6
Ответ: (-∞;6)
Слайд 11Уравнение вида | f(x)| =| g(x) |
| f(x)| =| g(x) |
Заменяем
f(x)2 = g(x)2
f(x)2 - g(x)2=0
(f(x) - g(x))(f(x) +g(x)) =0
f(x) - g(x)=0 или f(x) +g(x) =0
Слайд 12|2x+5|=|3x-1|
(2x+5)2 =(3x-1)2
(2x+5)2 -(3x-1)2 =0
((2x+5)-(3x-1))((2x+5)+(3x-1))=0
(2x+5)-(3x-1)=0 или (2x+5)+(3x-1)=0
2x+5-3x+1=0
-x=-6 5x=-4
X=6 x=-0,8
Ответ: 6; -0,8
Решить уравнение |2x+5|=|3x-1|