- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Линейная алгебра. Матрицы презентация
Содержание
- 1. Линейная алгебра. Матрицы
- 2. Матрица Прямоугольная таблица чисел или символов, их
- 3. Матрица размера m×n
- 4. Главная диагональ Элементы матрицы, у которых номер строки равен номеру столбца
- 5. Равные матрицы Матрицы называются равными, если равны
- 6. Квадратная матрица Матрица, число строк которой равно
- 7. Диагональная матрица Квадратная матрица, у которой все
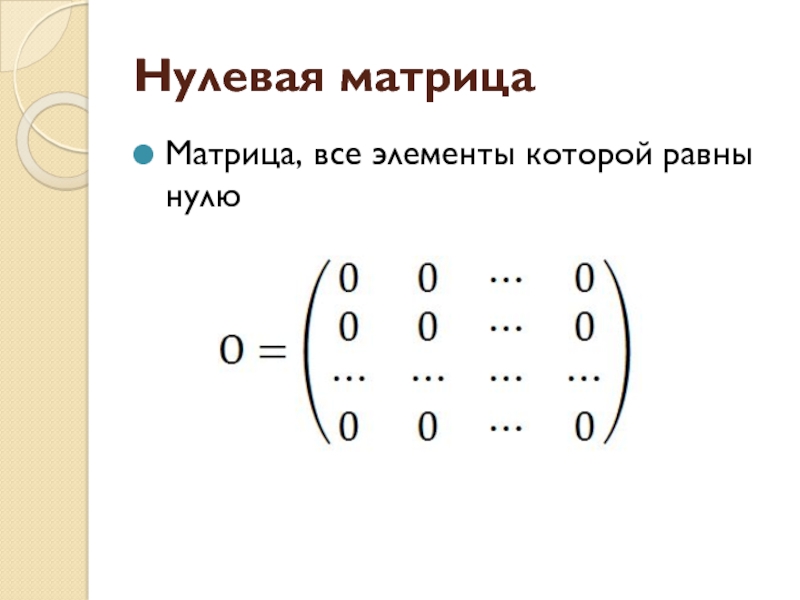
- 8. Нулевая матрица Матрица, все элементы которой равны нулю
- 9. Единичная матрица Диагональная матрица, каждый элемент главной диагонали равен единице
- 10. Треугольная матрица Квадратная матрица, у которой все
- 11. Вектор Матрица, состоящая из одного столбца (вектор-столбец) или одной строки (вектор- строка)
- 12. ОПЕРАЦИИ НАД МАТРИЦАМИ
- 13. Транспонирование Меняем местами строки и столбцы
- 14. Пример
- 15. Сложение матриц Матрицы одного размера!!!
- 16. Пример
- 17. Умножение матрицы на число
- 18. Пример
- 19. Умножение матриц Количество столбцов в первой матрице равно количеству строк во второй
- 20. Умножение матриц СТРОКА НА СТОЛБЕЦ
- 21. Пример
- 22. Задача Найти линейную комбинацию матриц
- 23. ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ МАТРИЦ
- 24. Элементарные преобразования матриц = эквивалентные преобразования матриц А~В
- 25. Перестановка местами двух строк (столбцов) матрицы
- 26. Умножение всех элементов строки (столбца) на число ≠ 0
- 27. Прибавление ко всем элементам строки (столбца) соответствующих
- 28. К первой строке прибавим вторую, умноженную на 10
- 29. СВОЙСТВА ОПЕРАЦИЙ НАД МАТРИЦАМИ
- 30. 1. Коммутативность А + В =
- 31. 2. Ассоциативность (А + В) +
- 32. 3. Дистрибутивность α(А + В) = α
- 33. 4.Наличие нейтрального элемента А + О =
- 34. 5. Для операции транспонирования (А +
- 35. Канонический вид матрицы Матрица имеет канонический вид,
- 36. Любую матрицу с помощью эквивалентных преобразований можно привести к каноническому виду
- 37. Ранг матрицы Количество линейно независимых строк (столбцов) матрицы rang (A) или r(A)
- 38. Свойства ранга матрицы 1. При транспонировании
- 39. Ранг канонической матрицы = количеству единиц на главной диагонали
- 40. След квадратной матрицы Сумма её диагональных элементов
- 41. Симметричная матрица Квадратная матрица, у которой ∀ i ∀j aij = aji
Матрица Прямоугольная таблица чисел или символов, их заменяющих, из m строк (или n столбцов) одинаковой длины
Слайд 2Матрица
Прямоугольная таблица чисел или символов, их заменяющих, из m строк (или
n столбцов) одинаковой длины
Слайд 5Равные матрицы
Матрицы называются равными, если равны все соответствующие элементы этих матриц
А=В
∀i
∀j aij = bij
Слайд 6Квадратная матрица
Матрица, число строк которой равно числу столбцов
Количество строк =
= количество
столбцов = n
⇒ Квадратная матрица n-го порядка
⇒ Квадратная матрица n-го порядка
Слайд 7Диагональная матрица
Квадратная матрица, у которой все элементы, кроме элементов главной диагонали,
равны нулю
Слайд 10Треугольная матрица
Квадратная матрица, у которой все элементы, расположенные по одну сторону
от главной диагонали, равны нулю
Слайд 11Вектор
Матрица, состоящая из одного столбца (вектор-столбец) или одной строки (вектор- строка)
Слайд 27Прибавление ко всем элементам строки (столбца) соответствующих элементов другой строки (столбца),
умноженных на одно и то же число
Слайд 301. Коммутативность
А + В = В + А
Операция умножения матриц
не является коммутативной
А × В ≠ В × А
А × В ≠ В × А
Слайд 31 2. Ассоциативность
(А + В) + С = А + (В
+ С) =
= А + В + С
(А × В) × С = А × (В × С) =
= А × В × С
= А + В + С
(А × В) × С = А × (В × С) =
= А × В × С
Слайд 323. Дистрибутивность
α(А + В) = α А + α В
(α +
β)А = α А + β А
(α β)А = α (β А)
А × (В+С) = А ×В + А ×С
(А + В) × С = А ×С + В ×С
α(А × В) = (α А) × В
(α β)А = α (β А)
А × (В+С) = А ×В + А ×С
(А + В) × С = А ×С + В ×С
α(А × В) = (α А) × В
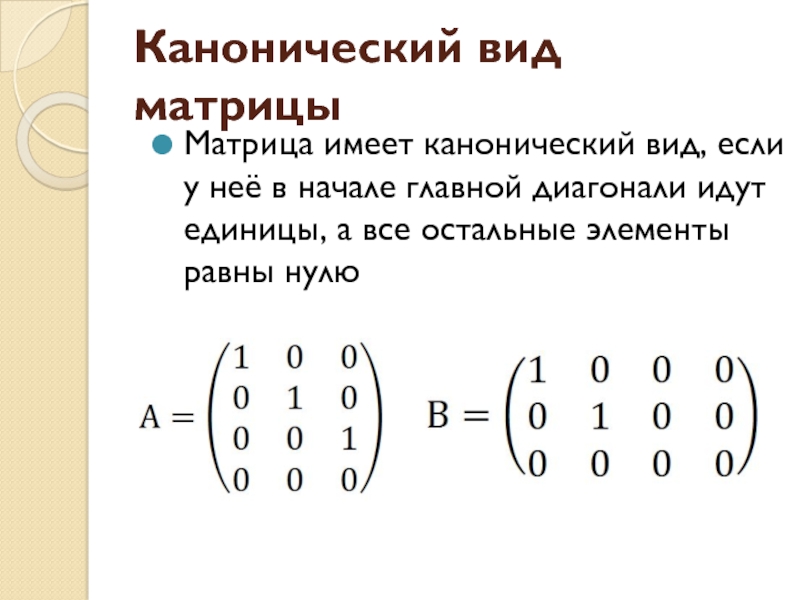
Слайд 35Канонический вид матрицы
Матрица имеет канонический вид, если у неё в начале
главной диагонали идут единицы, а все остальные элементы равны нулю
Слайд 38 Свойства ранга матрицы
1. При транспонировании матрицы её ранг не меняется
2.
Если вычеркнуть из матрицы нулевую строку (нулевой столбец), то её ранг не изменится
3. Ранг матрицы не изменяется при элементарных преобразованиях матрицы
3. Ранг матрицы не изменяется при элементарных преобразованиях матрицы
