повторить и обобщить знания учащихся по теме «Одночлены», «Умножение и возведение одночленов в степень».
Развивающие:
Способствовать развитию умения применять свойства степени к умножению одночленов.
Развивать интерес к предмету.
Воспитательные:
Воспитывать критическое отношение к своим знаниям, учить сравнивать, делать выводы.
Приучать учащихся пояснять свои решения, вырабатывать культуру математической речи.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Умножение одночленов. Возведение одночлена в степень презентация
Содержание
- 1. Умножение одночленов. Возведение одночлена в степень
- 2. Устная фронтальная работа На какие два вида
- 3. х2; -с; 3,4х2у; 0,5;
- 4. Назовите коэффициэнт одночлена и определите его степень
- 5. Назовите коэффициэнт одночлена и определите его степень
- 6. Назовите коэффициэнт одночлена и определите его степень
- 7. Назовите коэффициэнт одночлена и определите его степень
- 8. Назовите коэффициэнт одночлена и определите его степень
- 9. Назовите коэффициэнт одночлена и определите его степень
- 10. Назовите коэффициэнт одночлена и определите его степень
- 11. Назовите коэффициэнт одночлена и определите его степень
- 12. Назовите коэффициэнт одночлена и определите его степень
- 13. Назовите коэффициэнт одночлена и определите его степень
- 14. Назовите коэффициэнт одночлена и определите его степень
- 15. Назовите коэффициэнт одночлена и определите его степень
- 16. Назовите коэффициэнт одночлена и определите его степень
- 17. Назовите коэффициэнт одночлена и определите его степень
- 18. Назовите коэффициэнт одночлена и определите его степень
- 19. Назовите коэффициэнт одночлена и определите его степень
- 20. Назовите коэффициэнт одночлена и определите его степень
- 21. Назовите коэффициэнт одночлена и определите его степень
- 22. Назовите коэффициэнт одночлена и определите его степень
- 23. ИГРА: «Вычислительная пауза»
- 24. ИГРА: «Вычислительная пауза»
- 25. ИГРА: «Вычислительная пауза»
- 26. ИГРА: «Вычислительная пауза»
- 27. ИГРА: «Вычислительная пауза»
- 28. ИГРА: «Вычислительная пауза»
- 29. ИГРА: «Вычислительная пауза»
- 30. ИГРА: «Вычислительная пауза»
- 31. Диофант – греческий учёный Понятие степени
- 32. Приведите одночлен к стандартному виду: А) 5yy2y;
- 33. Приведите одночлен к стандартному виду: А) 5yy2y;
- 34. Приведите одночлен к стандартному виду: А) 5yy2y;
- 35. Приведите одночлен к стандартному виду: А) 5yy2y;
- 36. Приведите одночлен к стандартному виду: А) 5yy2y;
- 37. Приведите одночлен к стандартному виду: А) 5yy2y;
- 38. Приведите одночлен к стандартному виду: А) 5yy2y;
- 39. Приведите одночлен к стандартному виду: А) 5yy2y;
- 40. Приведите одночлен к стандартному виду: А) 5yy2y;
- 41. Выполняя задания на преобразование выражений, содержащих степени
- 42. Выполняя задания на преобразование выражений, содержащих степени
- 43. Выполняя задания на преобразование выражений, содержащих степени
- 44. Выполняя задания на преобразование выражений, содержащих степени
- 45. Выполняя задания на преобразование выражений, содержащих степени
- 46. Выполняя задания на преобразование выражений, содержащих степени
- 47. Выполняя задания на преобразование выражений, содержащих степени
- 48. Выполняя задания на преобразование выражений, содержащих степени
- 49. Физкультпауза Предлагается несколько вариантов ответов,
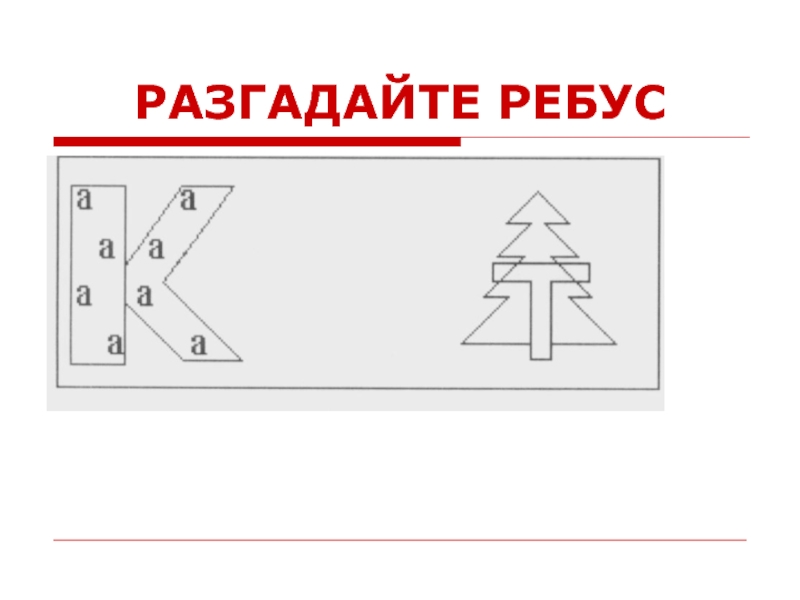
- 50. РАЗГАДАЙТЕ РЕБУС
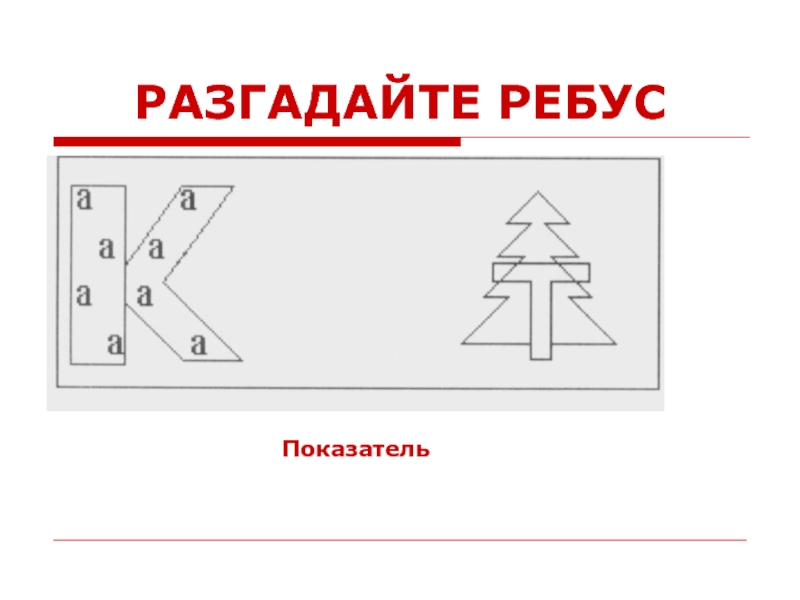
- 51. РАЗГАДАЙТЕ РЕБУС Показатель
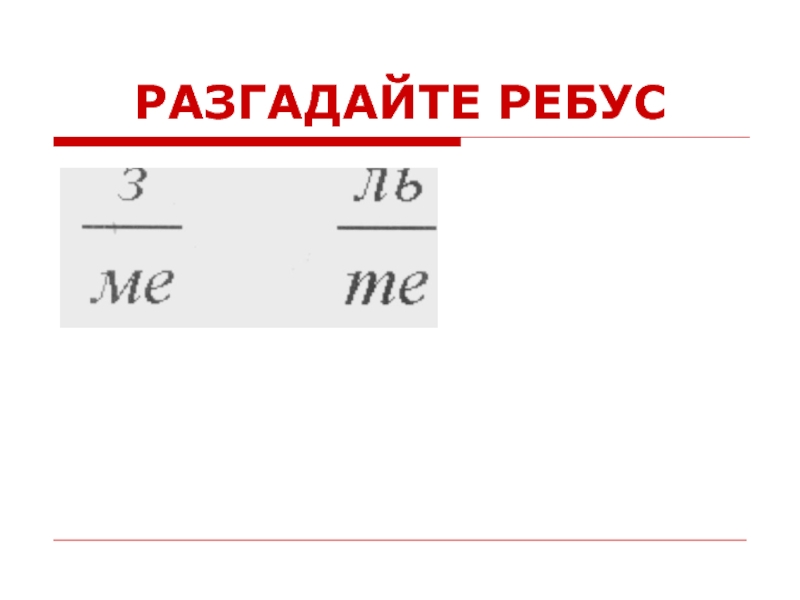
- 52. РАЗГАДАЙТЕ РЕБУС
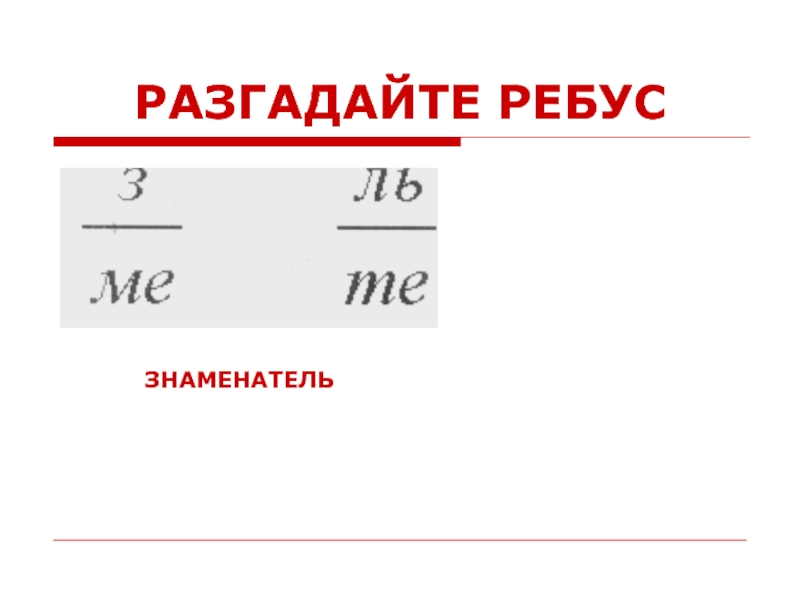
- 53. РАЗГАДАЙТЕ РЕБУС ЗНАМЕНАТЕЛЬ
Слайд 2Устная фронтальная работа
На какие два вида можно разделить эти выражения?
х2; 3+а; -с;
; x2y-3y; ;
3,4х2у; х2+х-1; 0,5; a-b;
х2•х; a•(-0,5).
3,4х2у; х2+х-1; 0,5; a-b;
х2•х; a•(-0,5).
Слайд 4Назовите коэффициэнт одночлена и определите его степень
8x2y; 3x5; -7xy; 6x2; 17;
-a5; y;
0,8mn3k2; ab2c3.
0,8mn3k2; ab2c3.
Слайд 5Назовите коэффициэнт одночлена и определите его степень
8x2y; 3x5; -7xy; 6x2; 17;
-a5; y;
0,8mn3k2; ab2c3.
КОЭФФИЦИЭНТЫ:
8.
0,8mn3k2; ab2c3.
КОЭФФИЦИЭНТЫ:
8.
Слайд 6Назовите коэффициэнт одночлена и определите его степень
8x2y; 3x5; -7xy; 6x2; 17;
-a5; y;
0,8mn3k2; ab2c3.
КОЭФФИЦИЭНТЫ:
8; 3.
0,8mn3k2; ab2c3.
КОЭФФИЦИЭНТЫ:
8; 3.
Слайд 7Назовите коэффициэнт одночлена и определите его степень
8x2y; 3x5; -7xy; 6x2; 17;
-a5; y;
0,8mn3k2; ab2c3.
КОЭФФИЦИЭНТЫ:
8; 3; -7.
0,8mn3k2; ab2c3.
КОЭФФИЦИЭНТЫ:
8; 3; -7.
Слайд 8Назовите коэффициэнт одночлена и определите его степень
8x2y; 3x5; -7xy; 6x2; 17;
-a5; y;
0,8mn3k2; ab2c3.
КОЭФФИЦИЭНТЫ:
8; 3; -7; 6.
0,8mn3k2; ab2c3.
КОЭФФИЦИЭНТЫ:
8; 3; -7; 6.
Слайд 9Назовите коэффициэнт одночлена и определите его степень
8x2y; 3x5; -7xy; 6x2; 17;
-a5; y;
0,8mn3k2; ab2c3.
КОЭФФИЦИЭНТЫ:
8; 3; -7; 6; 17.
0,8mn3k2; ab2c3.
КОЭФФИЦИЭНТЫ:
8; 3; -7; 6; 17.
Слайд 10Назовите коэффициэнт одночлена и определите его степень
8x2y; 3x5; -7xy; 6x2; 17;
-a5; y;
0,8mn3k2; ab2c3.
КОЭФФИЦИЭНТЫ:
8; 3; -7; 6; 17; -1.
0,8mn3k2; ab2c3.
КОЭФФИЦИЭНТЫ:
8; 3; -7; 6; 17; -1.
Слайд 11Назовите коэффициэнт одночлена и определите его степень
8x2y; 3x5; -7xy; 6x2; 17;
-a5; y;
0,8mn3k2; ab2c3.
КОЭФФИЦИЭНТЫ:
8; 3; -7; 6; 17; -1; 1.
0,8mn3k2; ab2c3.
КОЭФФИЦИЭНТЫ:
8; 3; -7; 6; 17; -1; 1.
Слайд 12Назовите коэффициэнт одночлена и определите его степень
8x2y; 3x5; -7xy; 6x2; 17;
-a5; y;
0,8mn3k2; ab2c3.
КОЭФФИЦИЭНТЫ:
8; 3; -7; 6; 17; -1; 1; 0,8.
0,8mn3k2; ab2c3.
КОЭФФИЦИЭНТЫ:
8; 3; -7; 6; 17; -1; 1; 0,8.
Слайд 13Назовите коэффициэнт одночлена и определите его степень
8x2y; 3x5; -7xy; 6x2; 17;
-a5; y;
0,8mn3k2; ab2c3.
КОЭФФИЦИЭНТЫ:
8; 3; -7; 6; 17; -1; 1; 0,8;1.
0,8mn3k2; ab2c3.
КОЭФФИЦИЭНТЫ:
8; 3; -7; 6; 17; -1; 1; 0,8;1.
Слайд 14Назовите коэффициэнт одночлена и определите его степень
8x2y; 3x5; -7xy; 6x2; 17;
-a5; y;
0,8mn3k2; ab2c3;
КОЭФФИЦИЭНТЫ:
8; 3; -7; 6; 17; -1; 1; 0,8;1.
СТЕПЕНЬ:
3.
0,8mn3k2; ab2c3;
КОЭФФИЦИЭНТЫ:
8; 3; -7; 6; 17; -1; 1; 0,8;1.
СТЕПЕНЬ:
3.
Слайд 15Назовите коэффициэнт одночлена и определите его степень
8x2y; 3x5; -7xy; 6x2; 17;
-a5; y;
0,8mn3k2; ab2c3;
КОЭФФИЦИЭНТЫ:
8; 3; -7; 6; 17; -1; 1; 0,8;1.
СТЕПЕНЬ:
3; 5.
0,8mn3k2; ab2c3;
КОЭФФИЦИЭНТЫ:
8; 3; -7; 6; 17; -1; 1; 0,8;1.
СТЕПЕНЬ:
3; 5.
Слайд 16Назовите коэффициэнт одночлена и определите его степень
8x2y; 3x5; -7xy; 6x2; 17;
-a5; y;
0,8mn3k2; ab2c3;
КОЭФФИЦИЭНТЫ:
8; 3; -7; 6; 17; -1; 1; 0,8;1.
СТЕПЕНЬ:
3; 5; 2.
0,8mn3k2; ab2c3;
КОЭФФИЦИЭНТЫ:
8; 3; -7; 6; 17; -1; 1; 0,8;1.
СТЕПЕНЬ:
3; 5; 2.
Слайд 17Назовите коэффициэнт одночлена и определите его степень
8x2y; 3x5; -7xy; 6x2; 17;
-a5; y;
0,8mn3k2; ab2c3;
КОЭФФИЦИЭНТЫ:
8; 3; -7; 6; 17; -1; 1; 0,8;1.
СТЕПЕНЬ:
3; 5; 2; 2.
0,8mn3k2; ab2c3;
КОЭФФИЦИЭНТЫ:
8; 3; -7; 6; 17; -1; 1; 0,8;1.
СТЕПЕНЬ:
3; 5; 2; 2.
Слайд 18Назовите коэффициэнт одночлена и определите его степень
8x2y; 3x5; -7xy; 6x2; 17;
-a5; y;
0,8mn3k2; ab2c3;
КОЭФФИЦИЭНТЫ:
8; 3; -7; 6; 17; -1; 1; 0,8;1.
СТЕПЕНЬ:
3; 5; 2; 2; 0.
0,8mn3k2; ab2c3;
КОЭФФИЦИЭНТЫ:
8; 3; -7; 6; 17; -1; 1; 0,8;1.
СТЕПЕНЬ:
3; 5; 2; 2; 0.
Слайд 19Назовите коэффициэнт одночлена и определите его степень
8x2y; 3x5; -7xy; 6x2; 17;
-a5; y;
0,8mn3k2; ab2c3;
КОЭФФИЦИЭНТЫ:
8; 3; -7; 6; 17; -1; 1; 0,8;1.
СТЕПЕНЬ:
3; 5; 2; 2; 0; 5.
0,8mn3k2; ab2c3;
КОЭФФИЦИЭНТЫ:
8; 3; -7; 6; 17; -1; 1; 0,8;1.
СТЕПЕНЬ:
3; 5; 2; 2; 0; 5.
Слайд 20Назовите коэффициэнт одночлена и определите его степень
8x2y; 3x5; -7xy; 6x2; 17;
-a5; y;
0,8mn3k2; ab2c3;
КОЭФФИЦИЭНТЫ:
8; 3; -7; 6; 17; -1; 1; 0,8;1.
СТЕПЕНЬ:
3; 5; 2; 2; 0; 5; 1.
0,8mn3k2; ab2c3;
КОЭФФИЦИЭНТЫ:
8; 3; -7; 6; 17; -1; 1; 0,8;1.
СТЕПЕНЬ:
3; 5; 2; 2; 0; 5; 1.
Слайд 21Назовите коэффициэнт одночлена и определите его степень
8x2y; 3x5; -7xy; 6x2; 17;
-a5; y;
0,8mn3k2; ab2c3;
КОЭФФИЦИЭНТЫ:
8; 3; -7; 6; 17; -1; 1; 0,8;1.
СТЕПЕНЬ:
3; 5; 2; 2; 0; 5; 1; 6.
0,8mn3k2; ab2c3;
КОЭФФИЦИЭНТЫ:
8; 3; -7; 6; 17; -1; 1; 0,8;1.
СТЕПЕНЬ:
3; 5; 2; 2; 0; 5; 1; 6.
Слайд 22Назовите коэффициэнт одночлена и определите его степень
8x2y; 3x5; -7xy; 6x2; 17;
-a5; y;
0,8mn3k2; ab2c3;
КОЭФФИЦИЭНТЫ:
8; 3; -7; 6; 17; -1; 1; 0,8;1.
СТЕПЕНЬ:
3; 5; 2; 2; 0; 5; 1; 6; 6.
0,8mn3k2; ab2c3;
КОЭФФИЦИЭНТЫ:
8; 3; -7; 6; 17; -1; 1; 0,8;1.
СТЕПЕНЬ:
3; 5; 2; 2; 0; 5; 1; 6; 6.
Слайд 31Диофант – греческий учёный
Понятие степени с натуральным показателем сформировалось ещё у
древних народов. Квадрат и куб числа использовались для вычислений площадей и объёмов. Степени некоторых чисел использовались при решении отдельных задач учёными Древнего Египта и Вавилона.
В IIIв. Вышла книга греческого учёного Диофанта «Арифметика», в которой было положено начало введению буквенной символики.
Диофант ввёл символы для первых шести степеней неизвестного и обратные им величины.
В IIIв. Вышла книга греческого учёного Диофанта «Арифметика», в которой было положено начало введению буквенной символики.
Диофант ввёл символы для первых шести степеней неизвестного и обратные им величины.
Слайд 32Приведите одночлен к стандартному виду:
А) 5yy2y;
Б) 2x y·4xy2;
В) 10a2b2 ·(-1,2a3b3);
Г)
4ac2·0,5 a3c;
Д) a·12ab2;
Е) 0,5 x2y·(-xy);
Ж) (2x)2· (-7x7y3);
З) (a2b)3· (5ab)2.
Д) a·12ab2;
Е) 0,5 x2y·(-xy);
Ж) (2x)2· (-7x7y3);
З) (a2b)3· (5ab)2.
Слайд 33Приведите одночлен к стандартному виду:
А) 5yy2y;
5y4;
Б) 2x y·4xy2;
В) 10a2b2 ·(-1,2a3b3);
Г) 4ac2·0,5 a3c;
Д) a·12ab2;
Е) 0,5 x2y·(-xy);
Ж) (2x)2· (-7x7y3);
З) (a2b)3· (5ab)2.
Б) 2x y·4xy2;
В) 10a2b2 ·(-1,2a3b3);
Г) 4ac2·0,5 a3c;
Д) a·12ab2;
Е) 0,5 x2y·(-xy);
Ж) (2x)2· (-7x7y3);
З) (a2b)3· (5ab)2.
Слайд 34Приведите одночлен к стандартному виду:
А) 5yy2y;
5y4;
Б) 2x y·4xy2; 8x2y3;
В) 10a2b2 ·(-1,2a3b3);
Г) 4ac2·0,5 a3c;
Д) a·12ab2;
Е) 0,5 x2y·(-xy);
Ж) (2x)2· (-7x7y3);
З) (a2b)3· (5ab)2.
Б) 2x y·4xy2; 8x2y3;
В) 10a2b2 ·(-1,2a3b3);
Г) 4ac2·0,5 a3c;
Д) a·12ab2;
Е) 0,5 x2y·(-xy);
Ж) (2x)2· (-7x7y3);
З) (a2b)3· (5ab)2.
Слайд 35Приведите одночлен к стандартному виду:
А) 5yy2y;
5y4;
Б) 2x y·4xy2; 8x2y3;
В) 10a2b2·(-1,2a3b3); -12a5b5;
Г) 4ac2·0,5 a3c;
Д) a·12ab2;
Е) 0,5 x2y·(-xy);
Ж) (2x)2· (-7x7y3);
З) (a2b)3· (5ab)2.
Б) 2x y·4xy2; 8x2y3;
В) 10a2b2·(-1,2a3b3); -12a5b5;
Г) 4ac2·0,5 a3c;
Д) a·12ab2;
Е) 0,5 x2y·(-xy);
Ж) (2x)2· (-7x7y3);
З) (a2b)3· (5ab)2.
Слайд 36Приведите одночлен к стандартному виду:
А) 5yy2y;
5y4;
Б) 2x y·4xy2; 8x2y3;
В) 10a2b2·(-1,2a3b3); -12a5b5;
Г) 4ac2·0,5 a3c; 2a4c3;
Д) a·12ab2;
Е) 0,5 x2y·(-xy);
Ж) (2x)2· (-7x7y3);
З) (a2b)3· (5ab)2.
Б) 2x y·4xy2; 8x2y3;
В) 10a2b2·(-1,2a3b3); -12a5b5;
Г) 4ac2·0,5 a3c; 2a4c3;
Д) a·12ab2;
Е) 0,5 x2y·(-xy);
Ж) (2x)2· (-7x7y3);
З) (a2b)3· (5ab)2.
Слайд 37Приведите одночлен к стандартному виду:
А) 5yy2y;
5y4;
Б) 2x y·4xy2; 8x2y3;
В) 10a2b2·(-1,2a3b3); -12a5b5;
Г) 4ac2·0,5 a3c; 2a4c3;
Д) a·12ab2; 8a2b2.
Е) 0,5 x2y·(-xy);
Ж) (2x)2· (-7x7y3);
З) (a2b)3· (5ab)2.
Б) 2x y·4xy2; 8x2y3;
В) 10a2b2·(-1,2a3b3); -12a5b5;
Г) 4ac2·0,5 a3c; 2a4c3;
Д) a·12ab2; 8a2b2.
Е) 0,5 x2y·(-xy);
Ж) (2x)2· (-7x7y3);
З) (a2b)3· (5ab)2.
Слайд 38Приведите одночлен к стандартному виду:
А) 5yy2y;
5y4;
Б) 2x y·4xy2; 8x2y3;
В) 10a2b2·(-1,2a3b3); -12a5b5;
Г) 4ac2·0,5 a3c; 2a4c3;
Д) a·12ab2; 8a2b2;
Е) 0,5 x2y·(-xy); -0,5x3y2;
Ж) (2x)2· (-7x7y3);
З) (a2b)3· (5ab)2.
Б) 2x y·4xy2; 8x2y3;
В) 10a2b2·(-1,2a3b3); -12a5b5;
Г) 4ac2·0,5 a3c; 2a4c3;
Д) a·12ab2; 8a2b2;
Е) 0,5 x2y·(-xy); -0,5x3y2;
Ж) (2x)2· (-7x7y3);
З) (a2b)3· (5ab)2.
Слайд 39Приведите одночлен к стандартному виду:
А) 5yy2y;
5y4;
Б) 2x y·4xy2; 8x2y3;
В) 10a2b2·(-1,2a3b3); -12a5b5;
Г) 4ac2·0,5 a3c; 2a4c3;
Д) a·12ab2; 8a2b2;
Е) 0,5 x2y·(-xy); -0,5x3y2;
Ж) (2x)2· (-7x7y3); -28x9y3;
З) (a2b)3· (5ab)2.
Б) 2x y·4xy2; 8x2y3;
В) 10a2b2·(-1,2a3b3); -12a5b5;
Г) 4ac2·0,5 a3c; 2a4c3;
Д) a·12ab2; 8a2b2;
Е) 0,5 x2y·(-xy); -0,5x3y2;
Ж) (2x)2· (-7x7y3); -28x9y3;
З) (a2b)3· (5ab)2.
Слайд 40Приведите одночлен к стандартному виду:
А) 5yy2y;
5y4;
Б) 2x y·4xy2; 8x2y3;
В) 10a2b2·(-1,2a3b3); -12a5b5;
Г) 4ac2·0,5 a3c; 2a4c3;
Д) a·12ab2; 8a2b2;
Е) 0,5 x2y·(-xy); -0,5x3y2;
Ж) (2x)2· (-7x7y3); -28x9y3;
З) (a2b)3· (5ab)2. a6b325a2b2=25a8b5.
Б) 2x y·4xy2; 8x2y3;
В) 10a2b2·(-1,2a3b3); -12a5b5;
Г) 4ac2·0,5 a3c; 2a4c3;
Д) a·12ab2; 8a2b2;
Е) 0,5 x2y·(-xy); -0,5x3y2;
Ж) (2x)2· (-7x7y3); -28x9y3;
З) (a2b)3· (5ab)2. a6b325a2b2=25a8b5.
Слайд 41Выполняя задания на преобразование выражений, содержащих степени ученик допустил следующие ошибки.
а)
(2m3)3=2m9;
б) (-2x y3)2=-4x2y9;
в) (x3)2·(-x3)4=-x2+4=-x6;
г) (a3)2=a9;
д) 220:210=22;
е) 23·27=410;
ж) (-xy2b3)6=-x6y12b18.
б) (-2x y3)2=-4x2y9;
в) (x3)2·(-x3)4=-x2+4=-x6;
г) (a3)2=a9;
д) 220:210=22;
е) 23·27=410;
ж) (-xy2b3)6=-x6y12b18.
Слайд 42Выполняя задания на преобразование выражений, содержащих степени ученик допустил следующие ошибки.
а)
(2m3)3=2m9; 8m9;
б) (-2x y3)2=-4x2y9;
в) (x3)2·(-x3)4=-x2+4=-x6;
г) (a3)2=a9;
д) 220:210=22;
е) 23·27=410;
ж) (-xy2b3)6=-x6y12b18.
б) (-2x y3)2=-4x2y9;
в) (x3)2·(-x3)4=-x2+4=-x6;
г) (a3)2=a9;
д) 220:210=22;
е) 23·27=410;
ж) (-xy2b3)6=-x6y12b18.
Слайд 43Выполняя задания на преобразование выражений, содержащих степени ученик допустил следующие ошибки.
а)
(2m3)3=2m9; 8m9;
б) (-2x y3)2=-4x2y9; 4x2y6;
в) (x3)2·(-x3)4=-x2+4=-x6;
г) (a3)2=a9;
д) 220:210=22;
е) 23·27=410;
ж) (-xy2b3)6=-x6y12b18.
б) (-2x y3)2=-4x2y9; 4x2y6;
в) (x3)2·(-x3)4=-x2+4=-x6;
г) (a3)2=a9;
д) 220:210=22;
е) 23·27=410;
ж) (-xy2b3)6=-x6y12b18.
Слайд 44Выполняя задания на преобразование выражений, содержащих степени ученик допустил следующие ошибки.
а)
(2m3)3=2m9; 8m9;
б) (-2x y3)2=-4x2y9; 4x2y6;
в) (x3)2·(-x3)4=-x2+4=-x6; x18;
г) (a3)2=a9;
д) 220:210=22;
е) 23·27=410;
ж) (-xy2b3)6=-x6y12b18.
б) (-2x y3)2=-4x2y9; 4x2y6;
в) (x3)2·(-x3)4=-x2+4=-x6; x18;
г) (a3)2=a9;
д) 220:210=22;
е) 23·27=410;
ж) (-xy2b3)6=-x6y12b18.
Слайд 45Выполняя задания на преобразование выражений, содержащих степени ученик допустил следующие ошибки.
а)
(2m3)3=2m9; 8m9;
б) (-2x y3)2=-4x2y9; 4x2y6;
в) (x3)2·(-x3)4=-x2+4=-x6; x18;
г) (a3)2=a9; a6;
д) 220:210=22;
е) 23·27=410;
ж) (-xy2b3)6=-x6y12b18.
б) (-2x y3)2=-4x2y9; 4x2y6;
в) (x3)2·(-x3)4=-x2+4=-x6; x18;
г) (a3)2=a9; a6;
д) 220:210=22;
е) 23·27=410;
ж) (-xy2b3)6=-x6y12b18.
Слайд 46Выполняя задания на преобразование выражений, содержащих степени ученик допустил следующие ошибки.
а)
(2m3)3=2m9; 8m9;
б) (-2x y3)2=-4x2y9; 4x2y6;
в) (x3)2·(-x3)4=-x2+4=-x6; x18;
г) (a3)2=a9; a6;
д) 220:210=22; 210;
е) 23·27=410;
ж) (-xy2b3)6=-x6y12b18.
б) (-2x y3)2=-4x2y9; 4x2y6;
в) (x3)2·(-x3)4=-x2+4=-x6; x18;
г) (a3)2=a9; a6;
д) 220:210=22; 210;
е) 23·27=410;
ж) (-xy2b3)6=-x6y12b18.
Слайд 47Выполняя задания на преобразование выражений, содержащих степени ученик допустил следующие ошибки.
а)
(2m3)3=2m9; 8m9;
б) (-2x y3)2=-4x2y9; 4x2y6;
в) (x3)2·(-x3)4=-x2+4=-x6; x18;
г) (a3)2=a9; a6;
д) 220:210=22; 210;
е) 23·27=410; 210;
ж) (-xy2b3)6=-x6y12b18.
б) (-2x y3)2=-4x2y9; 4x2y6;
в) (x3)2·(-x3)4=-x2+4=-x6; x18;
г) (a3)2=a9; a6;
д) 220:210=22; 210;
е) 23·27=410; 210;
ж) (-xy2b3)6=-x6y12b18.
Слайд 48Выполняя задания на преобразование выражений, содержащих степени ученик допустил следующие ошибки.
а)
(2m3)3=2m9; 8m9;
б) (-2x y3)2=-4x2y9; 4x2y6;
в) (x3)2·(-x3)4=-x2+4=-x6; x18;
г) (a3)2=a9; a6;
д) 220:210=22; 210;
е) 23·27=410; 210;
ж) (-xy2b3)6=-x6y12b18. x6y12b18.
б) (-2x y3)2=-4x2y9; 4x2y6;
в) (x3)2·(-x3)4=-x2+4=-x6; x18;
г) (a3)2=a9; a6;
д) 220:210=22; 210;
е) 23·27=410; 210;
ж) (-xy2b3)6=-x6y12b18. x6y12b18.
Слайд 49Физкультпауза
Предлагается несколько вариантов ответов, если ответ неверный, дети на вдохе
хлопают в ладоши
1 столбик: a2b; b; a; ab.
2 столбик: 10c4x; 5c4x3; 2c3x3; 10c4x3.
3 столбик: -4x8; xy; 4x2; 4x2y.
1 столбик: a2b; b; a; ab.
2 столбик: 10c4x; 5c4x3; 2c3x3; 10c4x3.
3 столбик: -4x8; xy; 4x2; 4x2y.