Геометрический подход
к задачам баллистики
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Геометрический подход к задачам баллистики презентация
Содержание
- 1. Геометрический подход к задачам баллистики
- 2. Законы равноускоренного движения в координатном виде:
- 3. Задача на оптимальное бросание камня
- 4. Классический способ решения
- 5. Подлесный Д.В., Александров Д.А. О движении тела,
- 6. Векторные уравнения:
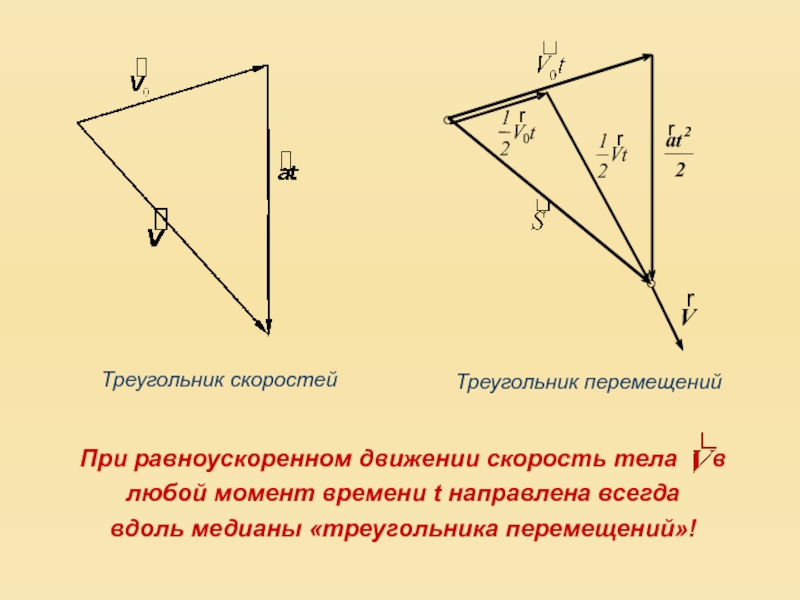
- 7. При равноускоренном движении скорость тела
- 9. При «оптимальном бросании» треугольник скоростей – прямоугольный, треугольник перемещений – равнобедренный!
- 10. Угол оптимального бросания
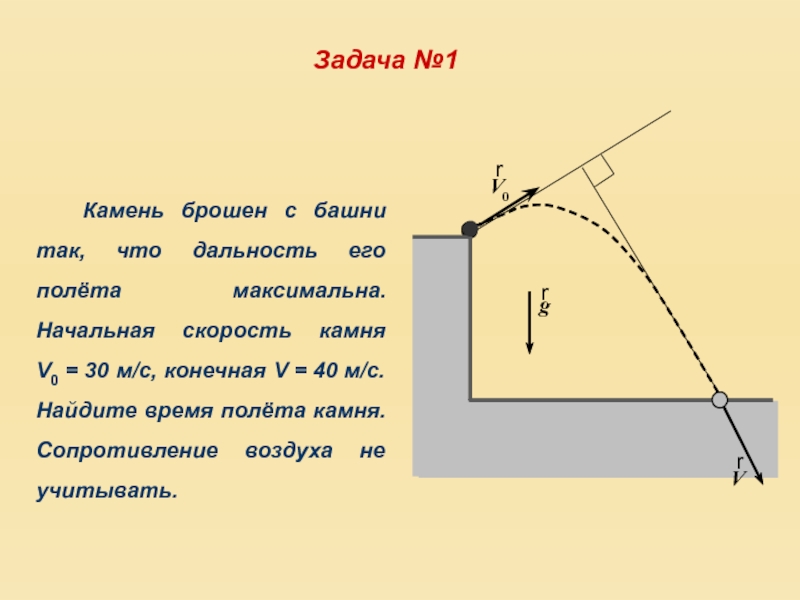
- 11. Камень брошен с башни так, что дальность
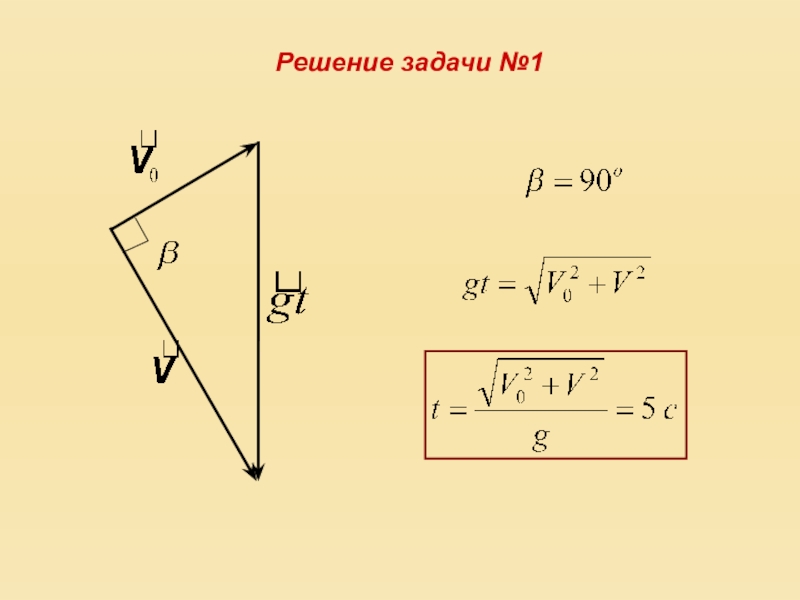
- 12. Решение задачи №1
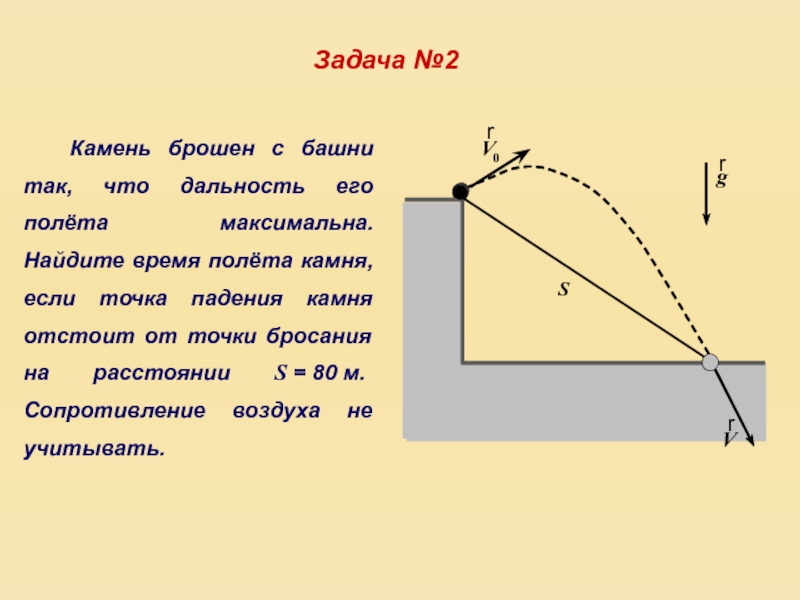
- 13. Камень брошен с башни так, что дальность
- 15. Задача №3 Камень бросают с горы, имеющей
- 16. Решение задачи №3
- 17. С вершины купола, имеющего форму полусферы и
- 18. x x y
- 19. C вершины купола, имеющего форму полусферы радиуса
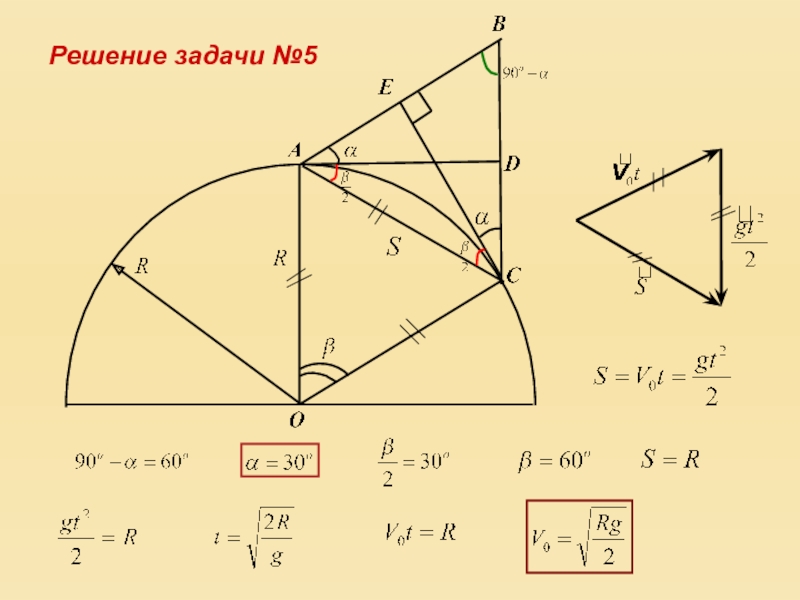
- 20. Решение задачи №5
Слайд 1
Д.В. Подлесный
научный руководитель ГБОУ Республики Мордовия
«Республиканский лицей для одарённых
детей»
Слайд 3Задача на оптимальное бросание камня
1. Как нужно бросить камень,
чтобы дальность полета L была максимальна?
2. Как нужно бросить камень, чтобы попасть в цель при минимальной начальной скорости?
2. Как нужно бросить камень, чтобы попасть в цель при минимальной начальной скорости?
Слайд 5 Подлесный Д.В., Александров Д.А. О движении тела, брошенного под углом к
горизонту // Потенциал, 2010. – №1. – С.25-30.
Слайд 7При равноускоренном движении скорость тела в любой момент времени
t направлена всегда
вдоль медианы «треугольника перемещений»!
Слайд 9При «оптимальном бросании» треугольник скоростей – прямоугольный, треугольник перемещений – равнобедренный!
Слайд 11Камень брошен с башни так, что дальность его полёта максимальна. Начальная
скорость камня V0 = 30 м/с, конечная V = 40 м/с. Найдите время полёта камня. Сопротивление воздуха не учитывать.
Задача №1
Слайд 13Камень брошен с башни так, что дальность его полёта максимальна. Найдите
время полёта камня, если точка падения камня отстоит от точки бросания на расстоянии S = 80 м. Сопротивление воздуха не учитывать.
r
0
V
V
r
S
Задача №2
Слайд 15Задача №3
Камень бросают с горы, имеющей постоянный угол наклона γ к
горизонту. Под каким углом α к поверхности горы нужно бросить камень, чтобы дальность его полета S была максимальной?
Слайд 17С вершины купола, имеющего форму полусферы и стоящего на горизонтальной поверхности
земли, бросили камень. Под каким углом α к горизонту был брошен камень, если известно, что в полёте он коснулся купола в некоторой точке Р? Радиус купола, проведённый к этой точке, образует угол β с вертикалью. Сопротивление воздуха не учитывать.
Задача №4
Слайд 19C вершины купола, имеющего форму полусферы радиуса R и стоящего на
горизонтальной поверхности земли, бросают камень. С какой минимальной скоростью V0 можно бросить, чтобы в процессе своего полёта он не ударился о поверхность купола? Под каким углом α к горизонту его следует бросать при этом? Сопротивление воздуха не учитывать. Касание поверхности купола допускается.
Задача №5