- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Умножение многочленов. Формулы сокращенного умножения презентация
Содержание
- 1. Умножение многочленов. Формулы сокращенного умножения
- 2. Три пути ведут к познанию: путь
- 3. Устный счет: Найти квадрат выражений
- 4. Работа над проектом: упростить выражение и сделать
- 5. Реализации продукта: Попробуйте записать формулы для выполнения
- 6. Закрепление: (a - b)(a + b) =
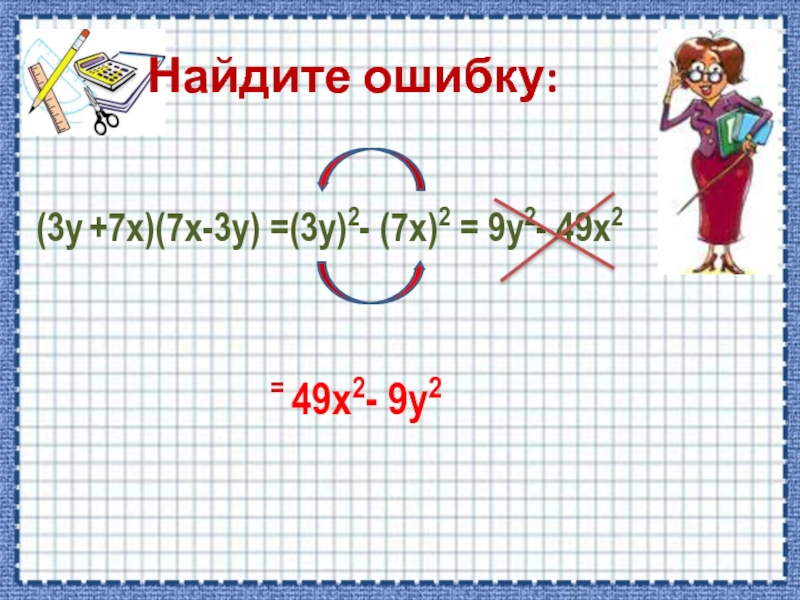
- 7. Найдите ошибку:
- 8. Выписать выражения, которые можно представить в виде
- 9. Вычислите значения произведений
- 10. Упростить выражение: (4х – 3)(4х +
- 11. Самостоятельная работа преобразуйте в многочлен и внесите
- 12. Семиотика Семио́тика, или семиоло́гия (от др.-греч. σημεῖον
- 13. Выучить правила п. 28. № №22(а,б),23(а,б),25(а,б),27 Домашнее задание:
- 14. До свидания! Спасибо за урок!
Слайд 2Три пути ведут к познанию: путь размышления – это путь самый
Слайд 3Устный счет:
Найти квадрат выражений
с;
2. Прочитайте выражение:
а) a2 + b2 ; б) (a + b)2 ;
в) (x - y)2; г) x2 – y2 д) (a - b)(a + b).
3. Выполнить умножение и упростить:
(x + 6)(x - 5) =
x2 - 5х + 6х – 30 =
x2 + х - 30.
4. Найти значение: 79*81; 42*38
? ? ?
Слайд 4Работа над проектом:
упростить выражение и сделать вывод:
(c – d)(c + d)
(m – n)(m + n) =
(a – b)(a + b) =
(y+ x)(x – y) =
(k – f)(k+ f) =
c2 + cd – cd – d2 = c2 – d2
m2 + mn – mn – n2 = m2 – n2
a2 + ab – ab – b2 = a2 – b2
xy –y2 + x2– xy = x2 – y2
k2 + kf – kf – f2 = k2 – f2
1. Какую закономерность вы заметили при решении этих заданий?
2. Что у них общего и в чём различие?
3. Какой вывод можно сделать?
4.Имеет ли смысл выполнять подробную запись решения подобных заданий?
5. Как вы думаете, важен ли порядок множителей в произведении? Почему?
Слайд 5Реализации продукта:
Попробуйте записать формулы для выполнения этих заданий в общем виде.
(a
Произведение разности двух выражений
на их сумму равно разности квадратов этих выражений.
Как прочитать формулы на обычном языке?
Слайд 6Закрепление:
(a - b)(a + b) = a2 - b2
Выполните умножение: п.
22(в,г)
в) (10m-4)(10m+4)=
г) (8а-1)(8а+1)=
23(в,г)
в) (4b+1)(1–4b)=
г) (5m+2)(5m–2)=
25(в,г)
в) (10p3-7q)(10p3+7q)=
г) (8d+6c3)(6c3-8d)=
Слайд 8Выписать выражения, которые можно представить в виде разности квадратов:
a2 - 9
x2
(a - b)(a + b) = a2 - b2
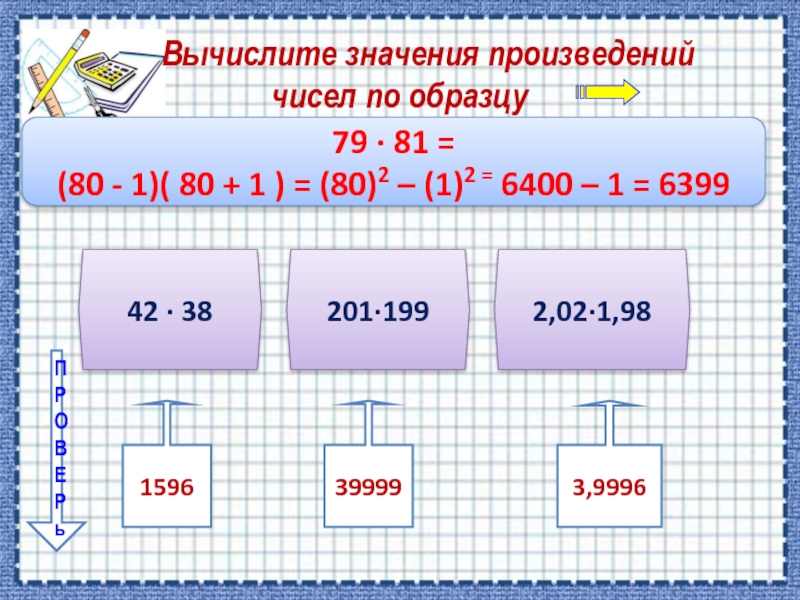
Слайд 9 Вычислите значения произведений
чисел по образцу
79 ∙
(80 - 1)( 80 + 1 ) = (80)2 – (1)2 = 6400 – 1 = 6399
42 ∙ 38
201∙199
2,02∙1,98
П
Р
О
В
Е
Р
ь
1596
39999
3,9996
Слайд 10Упростить выражение:
(4х – 3)(4х + 3) – (х + 2)(х –
16х2 – 9 – (х2– 4) =
16х2 – 9 – х2 + 4 =
15х2 – 5.
-
-
(a - b)(a + b) = a2 - b2
Слайд 11Самостоятельная работа
преобразуйте в многочлен и внесите букву, соответствующему ответу
А
Е
М
Т
С
К
О
И
И
Слайд 12Семиотика
Семио́тика, или семиоло́гия (от др.-греч. σημεῖον — «знак, признак»), — наука,
Знаки и символы в математике: «+» обозначает _______ , знак % заменяет слово ______, а знак є - _____. Использование знаков и символов дает возможность сделать записи короче и лаконичнее.