- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Начертательная геометрия. Взаимное пересечение поверхностей. (Лекция 8) презентация
Содержание
- 1. Начертательная геометрия. Взаимное пересечение поверхностей. (Лекция 8)
- 2. Взаимное пересечение поверхностей
- 3. Линией пересечения двух поверхностей , в общем
- 4. Φ ∩ Ω = l l{K1, K2,
- 5. Пересечение двух поверхностей может
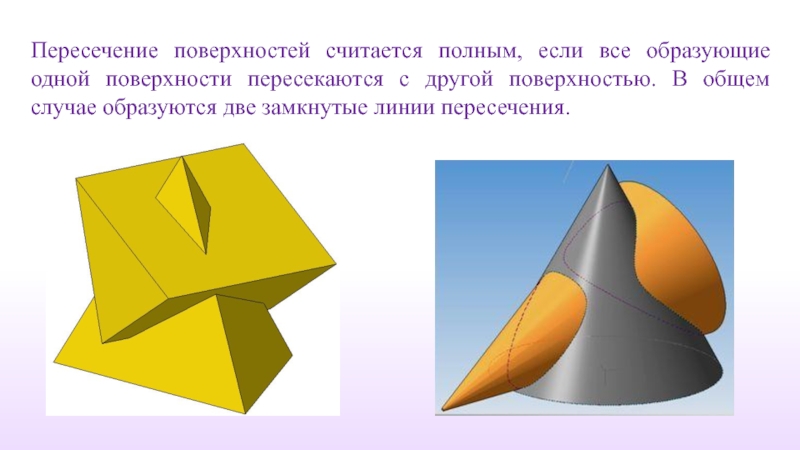
- 6. Пересечение поверхностей считается полным, если все образующие
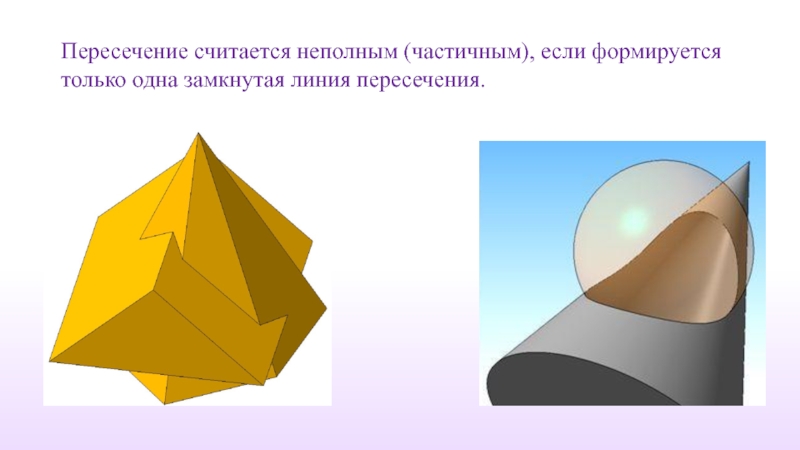
- 7. Пересечение считается неполным (частичным), если формируется только одна замкнутая линия пересечения.
- 8. Взаимное пересечение двух гранных поверхностей
- 9. Линией пересечения двух гранных поверхностей является ломаная
- 10. Определить какой тип пересечения поверхностей задан: полное
- 11. 2. Определить положение тел в пространстве.
- 12. 3. Обозначить явно заданные точки пересечения ребер
- 13. 4. Обозначить явно заданные точки пересечения ребер
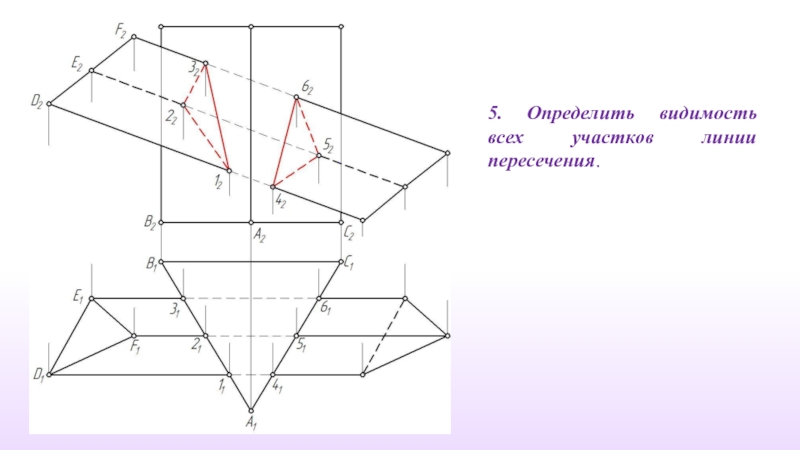
- 14. 5. Определить видимость всех участков линии пересечения.
- 15. Взаимное пересечение гранной поверхности с кривой поверхностью
- 16. Линия пересечения гранной поверхности с кривой поверхностью
- 17. Определить какой тип пересечения поверхностей задан: полное
- 18. 2. Определить положение тел в пространстве.
- 19. 3. Обозначить явно заданные точки 1, 2,
- 20. 4. Обозначить произвольные промежуточные точки 5 и
- 21. 5. Обозначить произвольные промежуточные точки 7 и
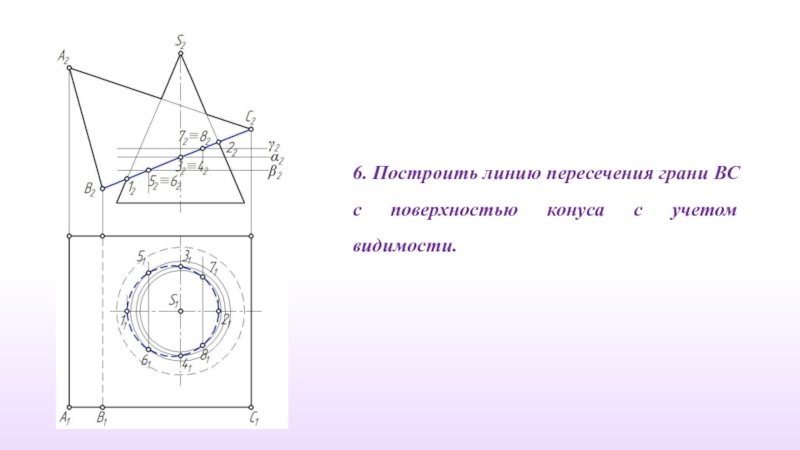
- 22. 6. Построить линию пересечения грани ВС с поверхностью конуса с учетом видимости.
- 23. 7. Обозначить явно заданные точки 9, 10,
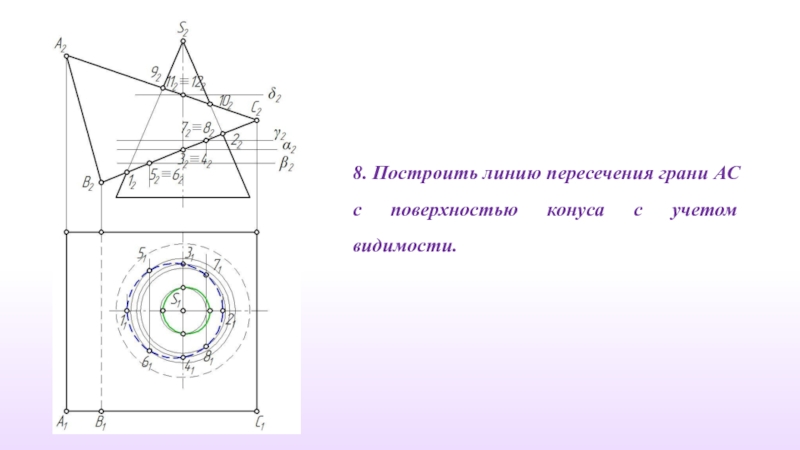
- 24. 8. Построить линию пересечения грани АС с поверхностью конуса с учетом видимости.
- 25. Взаимное пересечение кривых поверхностей
- 26. Линией пересечения двух кривых поверхностей является одна
- 27. Определение базовых точек линии пересечения К базовым
- 28. Определить какой тип пересечения поверхностей задан: полное
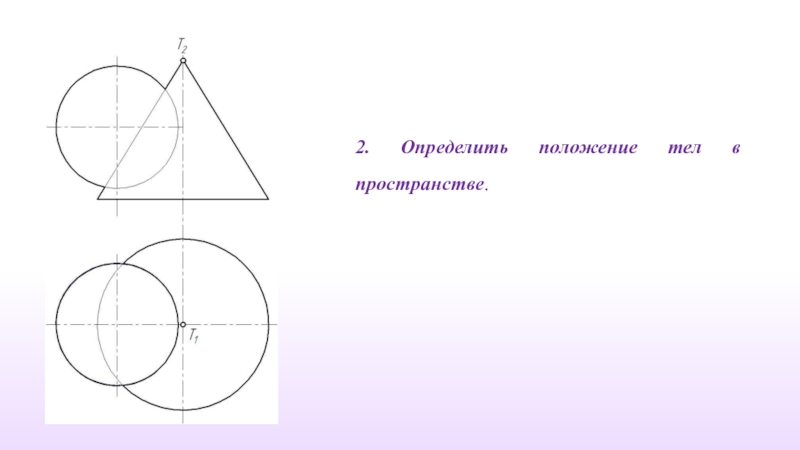
- 29. 2. Определить положение тел в пространстве.
- 30. 3. Обозначить базовые точки 1, 2, 3
- 31. 4. Обозначить произвольные промежуточные точки 5 и
- 32. 5. Обозначить произвольные промежуточные точки 7 и
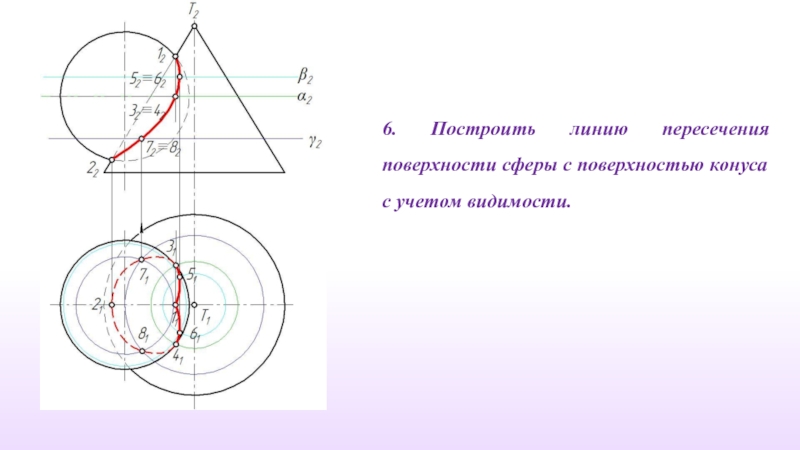
- 33. 6. Построить линию пересечения поверхности сферы с поверхностью конуса с учетом видимости.
- 34. Частные случаи взаимного пересечения двух поверхностей вращения
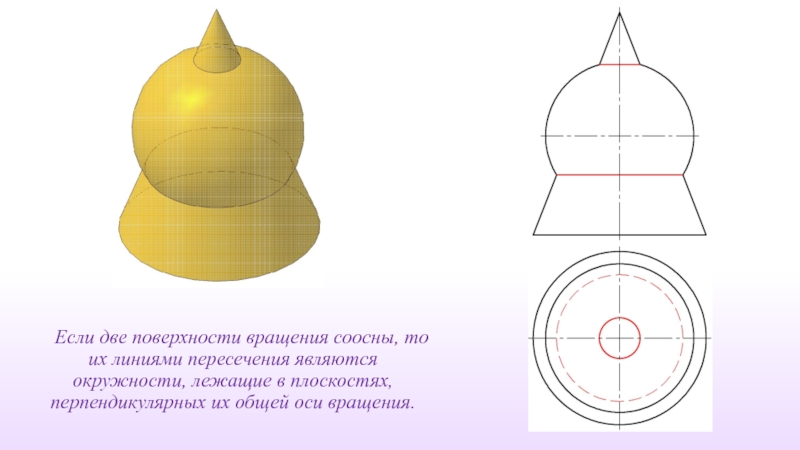
- 35. Если две поверхности вращения соосны, то их
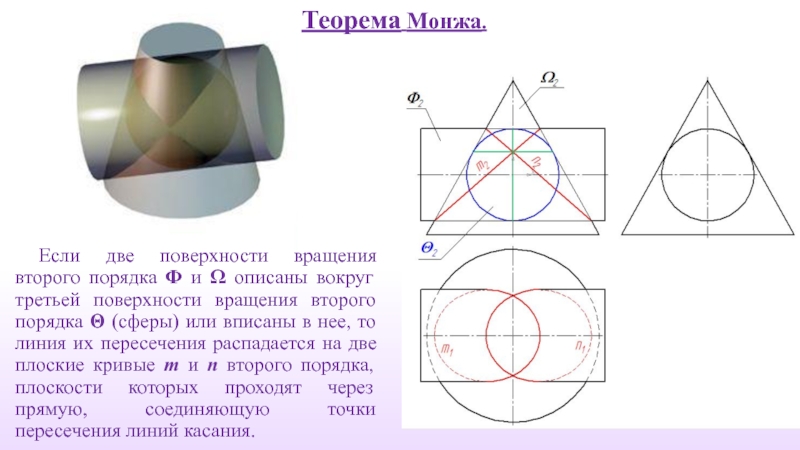
- 36. Если две поверхности вращения второго порядка Φ
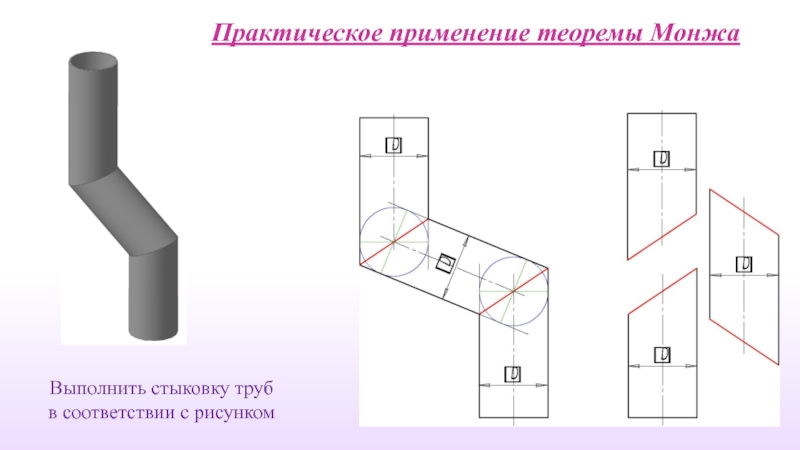
- 37. Практическое применение теоремы Монжа Выполнить стыковку труб в соответствии с рисунком
Слайд 3Линией пересечения двух поверхностей , в общем случае, является пространственная линия,
Обязательные требования, предъявляемые к секущим поверхностям-посредникам:
каждая из секущих поверхностей-посредников должна пересекать обе заданные поверхности;
линии, получаемые в результате пересечения должны пересекаться между собой и иметь, по возможности, наиболее простую геометрическую форму.
Слайд 4Φ ∩ Ω = l
l{K1, K2, K3,… Ki}
Ki = mi ∩
mi = Φ ∩ Σi
ni = Ω ∩ Σi
Σi – вспомогательная секущая поверхность-посредник
Слайд 5 Пересечение двух поверхностей может быть полным и неполным
Неполное пересечение называется врезанием.
Слайд 6Пересечение поверхностей считается полным, если все образующие одной поверхности пересекаются с
Слайд 7Пересечение считается неполным (частичным), если формируется только одна замкнутая линия пересечения.
Слайд 9Линией пересечения двух гранных поверхностей является ломаная прямая линия, точками излома
Т.е. вся задача на построение линии пересечения двух гранных поверхностей сводится к многократному решению задачи на определение точки пересечения прямой с плоскостью.
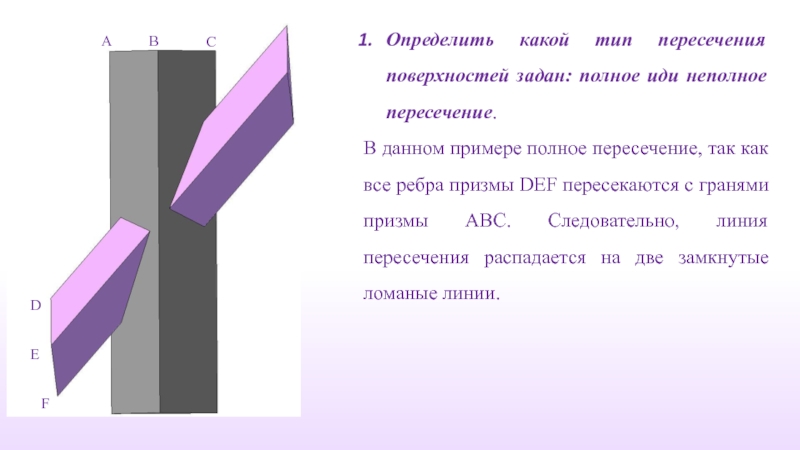
Слайд 10Определить какой тип пересечения поверхностей задан: полное иди неполное пересечение.
В
D
E
F
А
В
С
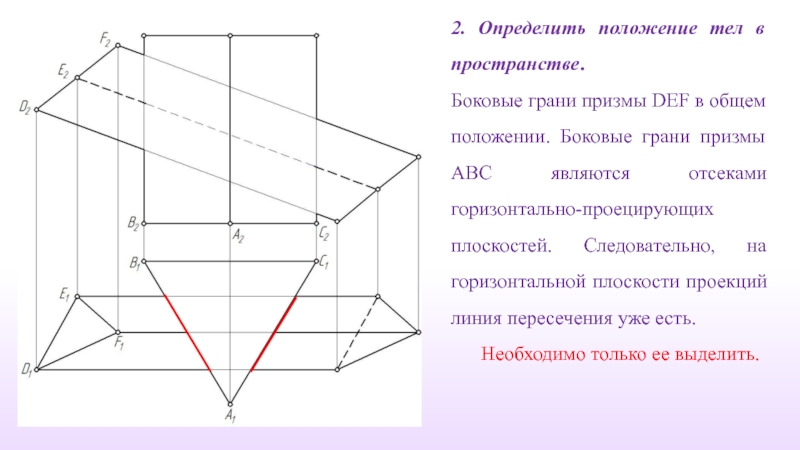
Слайд 112. Определить положение тел в пространстве.
Боковые грани призмы DEF в
Необходимо только ее выделить.
Слайд 123. Обозначить явно заданные точки пересечения ребер одного многогранника с гранью
Ребро D пересекается с гранью АВ в точке 1.
(D) ∩ АВ ≡ 1;
(E) ∩ АВ ≡ 2;
(F) ∩ АВ ≡ 3
Построить недостающие проекции выделенных точек.
Для облегчения чтения чертежа видимость точек можно не указывать.
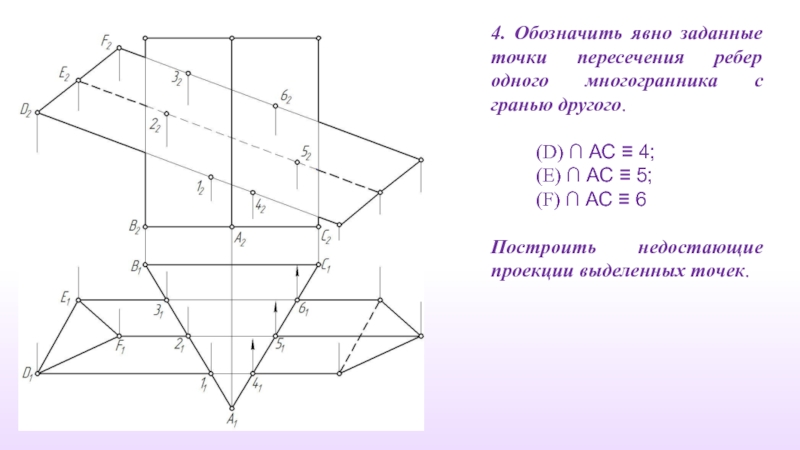
Слайд 134. Обозначить явно заданные точки пересечения ребер одного многогранника с гранью
(D) ∩ АС ≡ 4;
(E) ∩ АС ≡ 5;
(F) ∩ АС ≡ 6
Построить недостающие проекции выделенных точек.
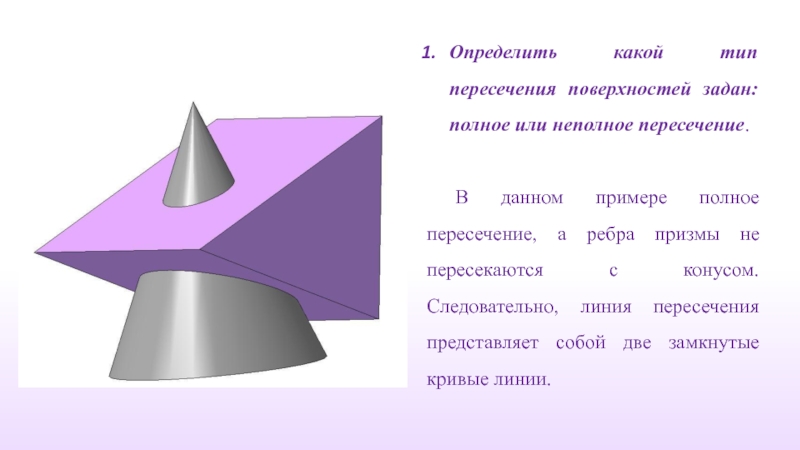
Слайд 16Линия пересечения гранной поверхности с кривой поверхностью представляет собой
ломаную кривую
кривую линию, если ребра гранной поверхности не пересекаются с кривой поверхностью.
Т.е. задача на построение линии пересечения гранной поверхности с кривой поверхностью сводится к многократному решению двух задач:
определение точек пересечения прямой линии с кривой поверхностью;
построение линии пересечения кривой поверхности плоскостью.
Слайд 17Определить какой тип пересечения поверхностей задан: полное или неполное пересечение.
В
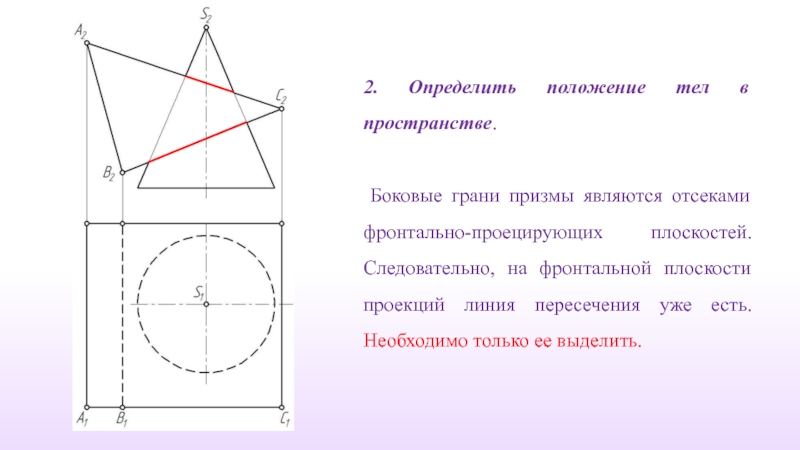
Слайд 182. Определить положение тел в пространстве.
Боковые грани призмы являются отсеками
Слайд 193. Обозначить явно заданные точки 1, 2, 3 и 4 пересечения
Опорные точки 1 и 2 на очерковых образующих.
Для нахождения точек 3 и 4 вводим вспомогательную плоскость-посредник
α ‖ π1
Построить недостающие проекции выделенных точек.
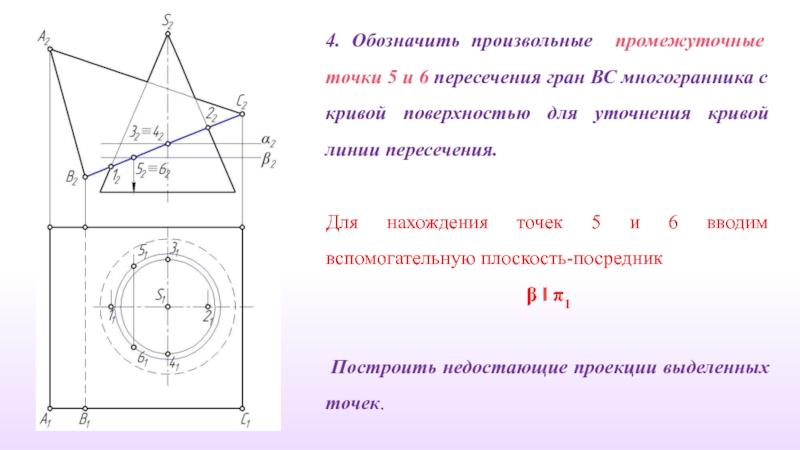
Слайд 204. Обозначить произвольные промежуточные точки 5 и 6 пересечения гран ВС
Для нахождения точек 5 и 6 вводим вспомогательную плоскость-посредник
β ‖ π1
Построить недостающие проекции выделенных точек.
Слайд 215. Обозначить произвольные промежуточные точки 7 и 8 пересечения грани ВС
Для нахождения точек 7 и 8 вводим вспомогательную плоскость-посредник
γ ‖ π1
Построить недостающие проекции выделенных точек.
Слайд 237. Обозначить явно заданные точки 9, 10, 11 и 12 пересечения
Опорные точки 9 и 10 на очерковых образующих.
Для нахождения точек 11 и 12 вводим вспомогательную плоскость-посредник
δ ‖ π1
Построить недостающие проекции выделенных точек.
Слайд 26Линией пересечения двух кривых поверхностей является одна или две пространственные (возможны
Для получения таких линий должны быть введены вспомогательные секущие поверхности-посредники как плоские, так и кривые.
Обязательные требования, предъявляемые к секущим поверхностям-посредникам:
каждая из секущих поверхностей-посредников должна пересекать обе заданные поверхности;
линии, получаемые в результате пересечения должны иметь наиболее простую геометрическую форму и попарно пересекаться между собой.
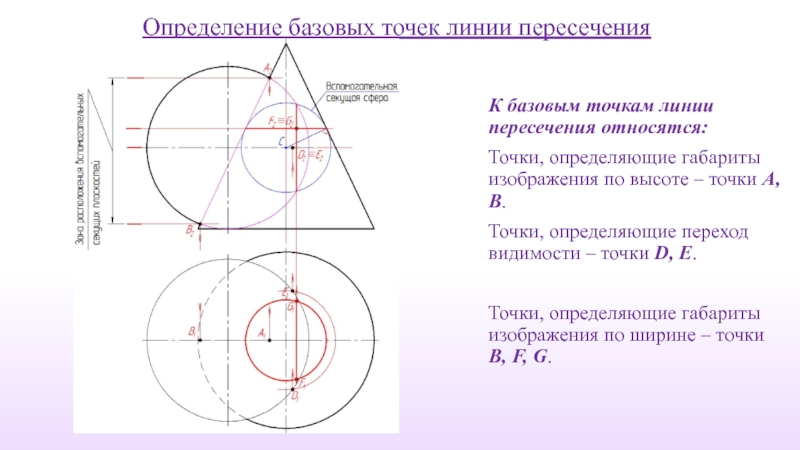
Слайд 27Определение базовых точек линии пересечения
К базовым точкам линии пересечения относятся:
Точки, определяющие
Точки, определяющие переход видимости – точки D, E.
Точки, определяющие габариты изображения по ширине – точки B, F, G.
Слайд 28Определить какой тип пересечения поверхностей задан: полное или неполное пересечение.
В
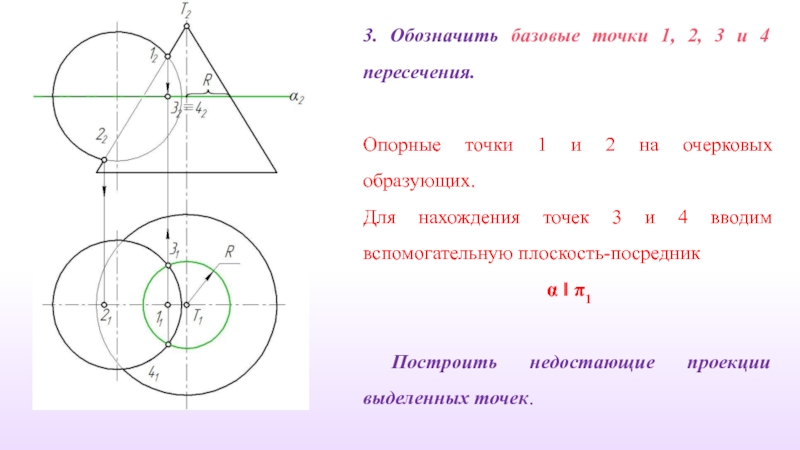
Слайд 303. Обозначить базовые точки 1, 2, 3 и 4 пересечения.
Опорные точки
Для нахождения точек 3 и 4 вводим вспомогательную плоскость-посредник
α ‖ π1
Построить недостающие проекции выделенных точек.
Слайд 314. Обозначить произвольные промежуточные точки 5 и 6 пересечения поверхностей для
Для нахождения точек 5 и 6 вводим вспомогательную плоскость-посредник
β ‖ π1
Построить недостающие проекции выделенных точек.
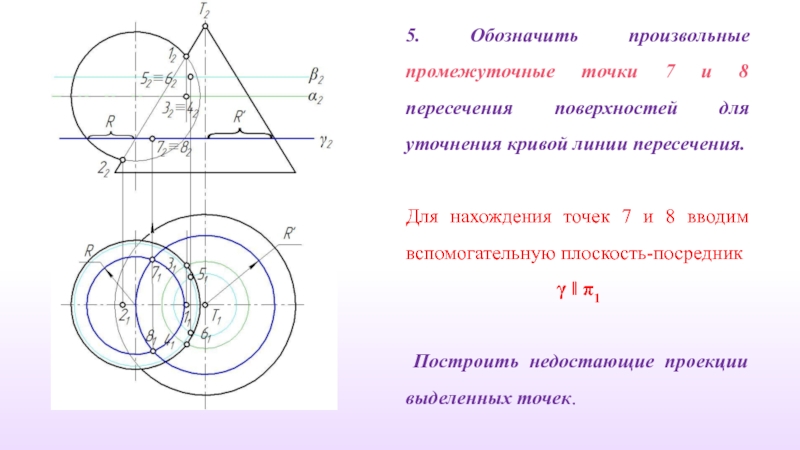
Слайд 325. Обозначить произвольные промежуточные точки 7 и 8 пересечения поверхностей для
Для нахождения точек 7 и 8 вводим вспомогательную плоскость-посредник
γ ‖ π1
Построить недостающие проекции выделенных точек.
Слайд 35Если две поверхности вращения соосны, то их линиями пересечения являются окружности,
Слайд 36Если две поверхности вращения второго порядка Φ и Ω описаны вокруг
Теорема Монжа.