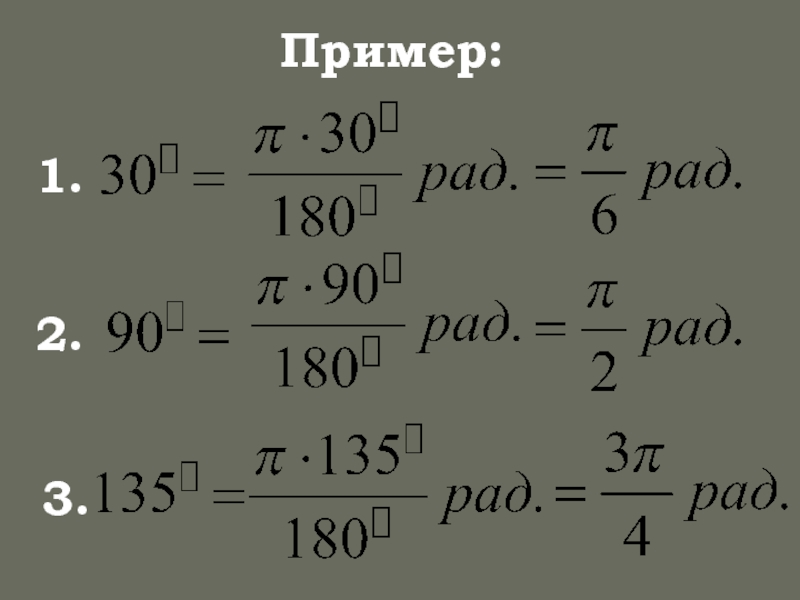- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Угол поворота. Радианная мера угла презентация
Содержание
- 1. Угол поворота. Радианная мера угла
- 2. Немного из истории… 1. Древние вавилоняне и
- 3. Немного из истории… 4. Насир ад-Дин Мухаммад
- 4. Тригонометрия раздел математики, изучающий соотношение сторон и
- 5. Градусная мера угла 1° – цена одного
- 6. Угол поворота х у 1 -1
- 7. Радианная мера угла у О
- 8. Заполните таблицу у О х
- 9. Пример: 1. 2. 3.
- 10. №1: Переведите в радианную меру углы: 1)
- 11. Пример: 1. 2. 3.
- 12. №2: Переведите в градусную меру углы: 1)
- 13. Самостоятельная работа 1. Переведите в радианную меру
- 14. Ответы 1) 2) 3) I вариант
Слайд 2Немного из истории…
1. Древние вавилоняне и египтяне изучали тригонометрию как часть
2. Древние индийцы: ввели названия «синус», «косинус», составили таблицы синусов, косинусов
3. IX-XVвв – Средний и Ближний восток: составляли таблицы котангенса, тангенса, косеканса; ввели понятие единичной окружности
Слайд 3Немного из истории…
4. Насир ад-Дин Мухаммад ат-Туси (1201-1274) выделил раздел тригонометрии
5. Лев Герсонид (1288-1344) – открыл теорему синусов
6. XVII-XIXвв: применение тригономет-рии в механике, физике, технике, как часть математического анализа (Виетт, Бернулли) – тригонометрические символы, графики – синусоиды
7. Л.Эйлер: придал тригонометрии современный вид
Слайд 4Тригонометрия
раздел математики, изучающий соотношение сторон и углов в треугольнике
(«три» - три,
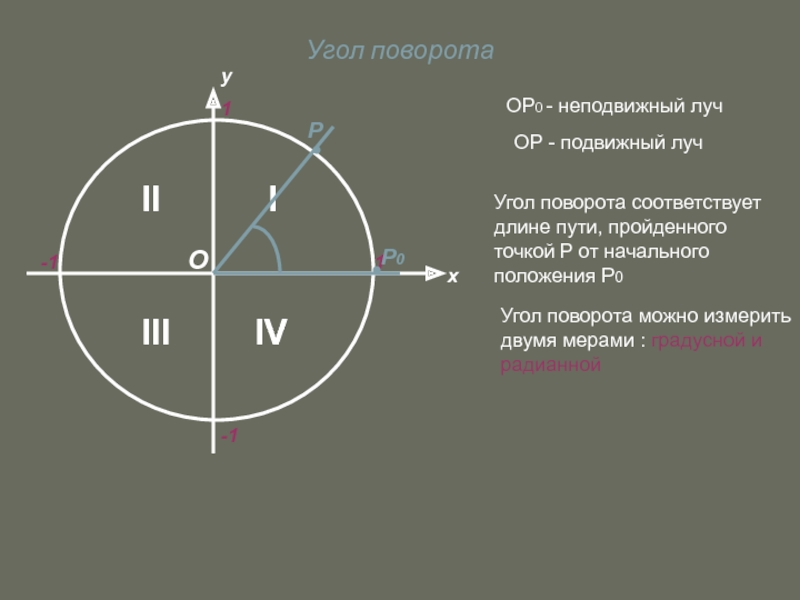
Слайд 6Угол поворота
х
у
1
-1
1
-1
II
IV
I
III
ОР0 - неподвижный луч
ОР - подвижный луч
Р
Р0
Угол поворота соответствует длине
Угол поворота можно измерить двумя мерами : градусной и радианной
О
Слайд 7
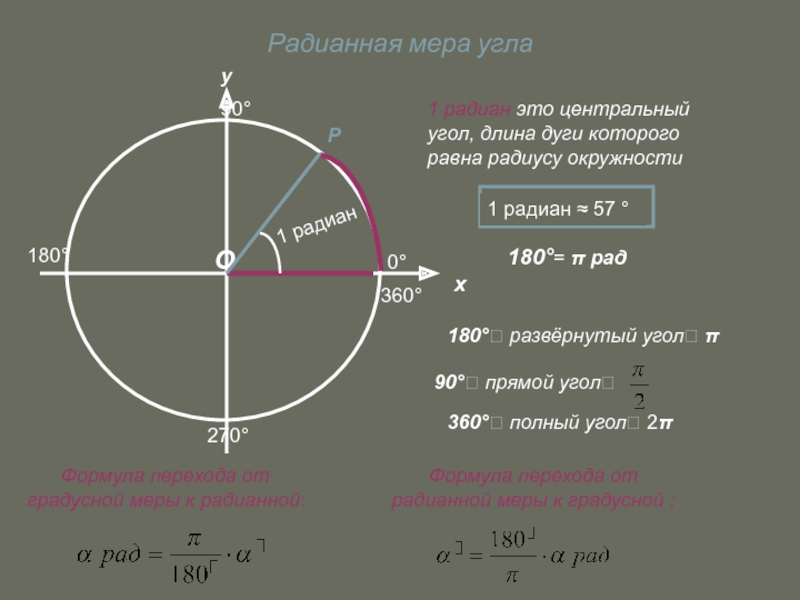
Радианная мера угла
у
О
Р
х
1 радиан это центральный угол, длина дуги которого равна
1 радиан
1 радиан ≈ 57 °
90°
270°
180°
0°
360°
180°= π рад
180°? развёрнутый угол? π
90°? прямой угол?
360°? полный угол? 2π
Формула перехода от радианной меры к градусной :
Формула перехода от градусной меры к радианной:
Слайд 8Заполните таблицу
у
О
х
90°
270°
180°
0°
360°
IV
III
II
I
интервал
четверть
0° < α < 90°
90 ° < α < 180 °
180° < α < 270°
I
II
IV
III
Определите, в какой четверти расположены углы:
α = 25°
β = - 100°
ϕ = 460°
γ = 220°
интервал в радианах
270° < α < 360°
α
β
γ
ϕ
Слайд 10№1: Переведите в радианную меру углы:
1) 45°
2) 15°
3) 72°
4) 100°
5) 200°
6) 360°
7) 215°
8) 150°
9) 330°
Слайд 13Самостоятельная работа
1. Переведите в радианную меру углы:
1) 60°
2) 145°
3)
I вариант
II вариант
1) 320°
2) 105°
3) 40°
2. Переведите в градусную меру углы:
1)
2)
1)
2)