Аналитическая статистика.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Статистическое изучение взаимосвязи социально-экономических явлений презентация
Содержание
- 1. Статистическое изучение взаимосвязи социально-экономических явлений
- 2. 2 Корреляционный и регрессионный анализ Основная
- 3. 3 Корреляционный и регрессионный анализ Предмет
- 4. 4 Корреляционный анализ Диаграмма рассеяния Простейшим
- 5. 5 Корреляционный анализ Линейный коэффициент корреляции Пирсона
- 6. Корреляционный анализ Линейный коэффициент корреляции Пирсона Основные свойства коэффициента корреляции: Нет линейной связи
- 7. 7 Корреляционный анализ Линейный коэффициент корреляции Пирсона
- 8. 8 Корреляционный анализ Линейный коэффициент корреляции Пирсона
- 9. 9 Корреляционный анализ Линейный коэффициент корреляции Пирсона
- 10. 10 Корреляционный анализ Проверка значимости коэффициента корреляции Линейный коэффициент корреляции для генеральной совокупности:
- 11. 11 Корреляционный анализ Проверка значимости коэффициента корреляции
- 12. 12 Корреляционный анализ Проверка значимости коэффициента корреляции
- 13. 13 Корреляционный анализ Проверка значимости коэффициента корреляции
- 14. 14 Регрессионный анализ Диаграмма рассеяния Наиболее
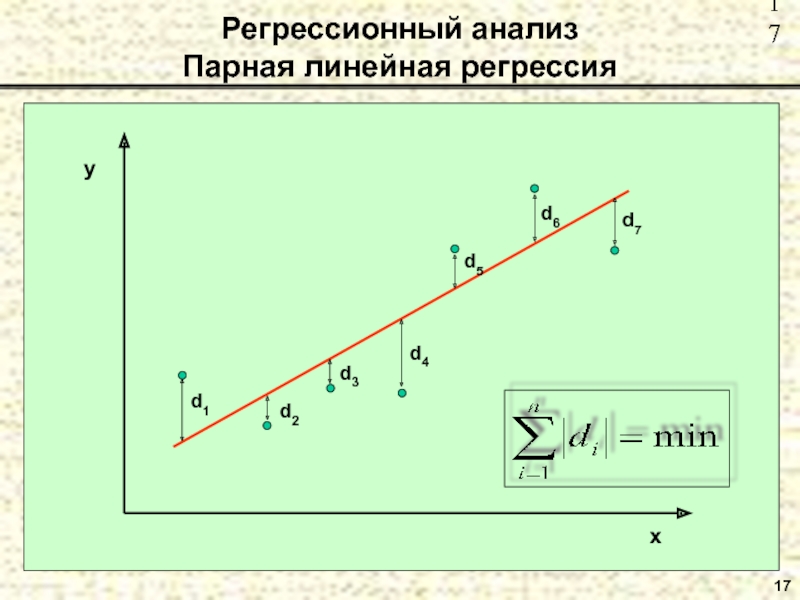
- 15. Регрессионный анализ Парная линейная регрессия
- 16. 16 Регрессионный анализ Парная линейная регрессия
- 17. 17 Регрессионный анализ Парная линейная регрессия
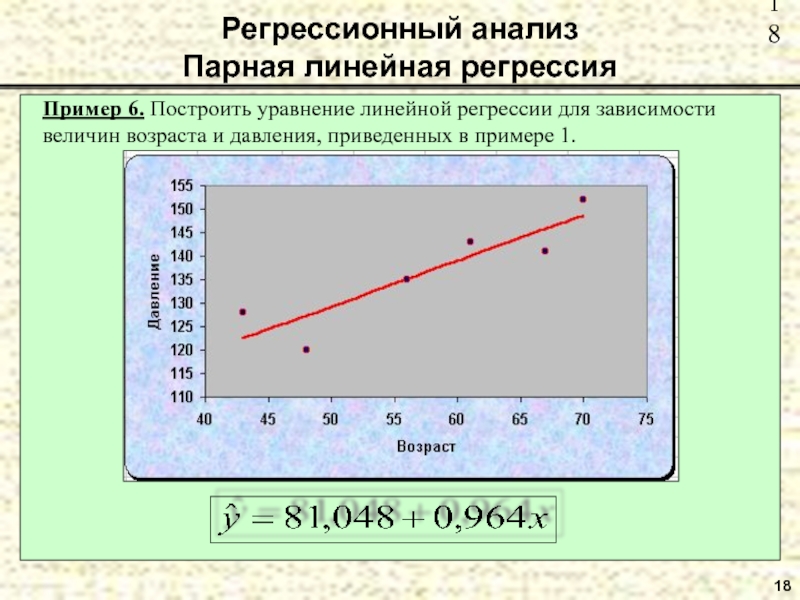
- 18. 18 Пример 6. Построить уравнение линейной
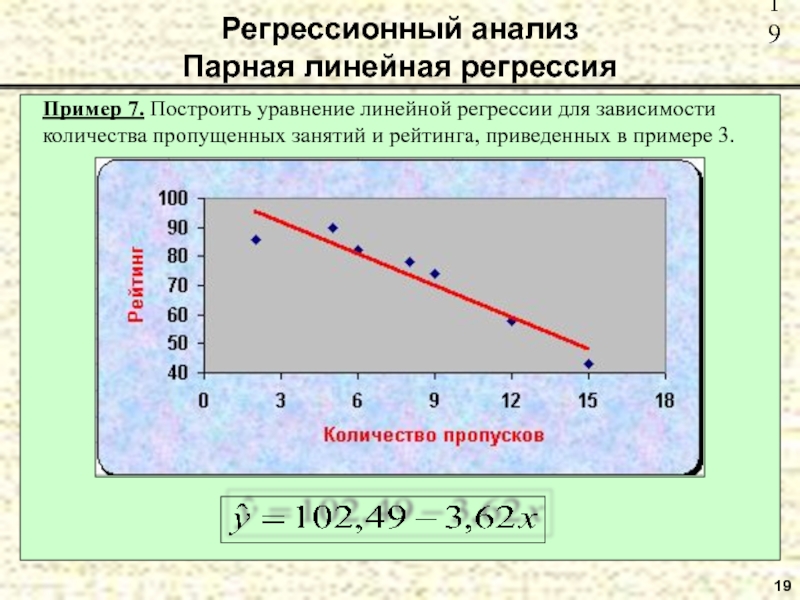
- 19. 19 Пример 7. Построить уравнение линейной
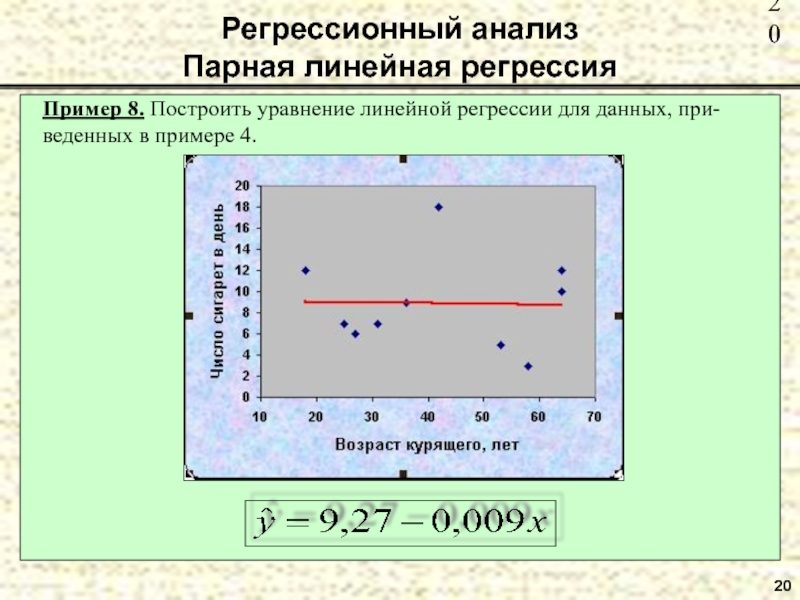
- 20. 20 Пример 8. Построить уравнение линейной
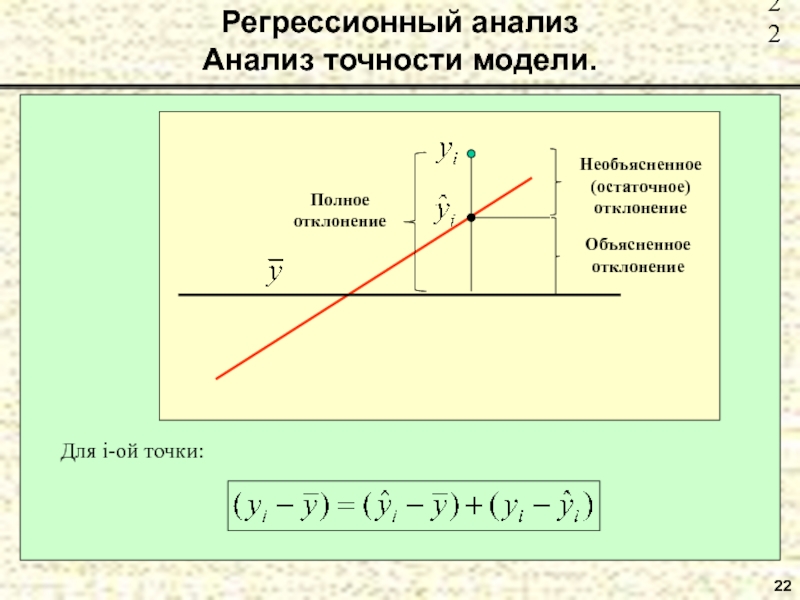
- 21. 21 Регрессионный анализ Анализ точности модели.
- 22. 22 Регрессионный анализ Анализ точности модели. Для i-ой точки:
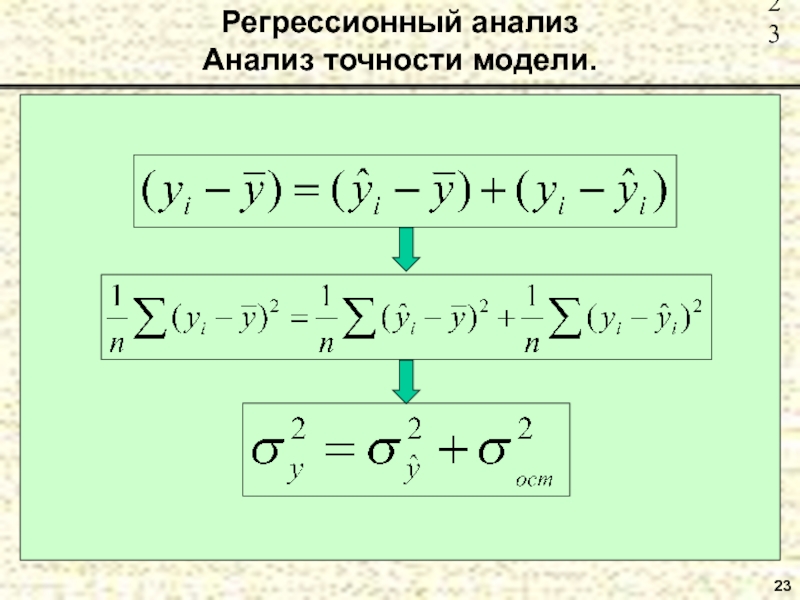
- 23. 23 Регрессионный анализ Анализ точности модели.
- 24. 24 Регрессионный анализ Анализ точности модели.
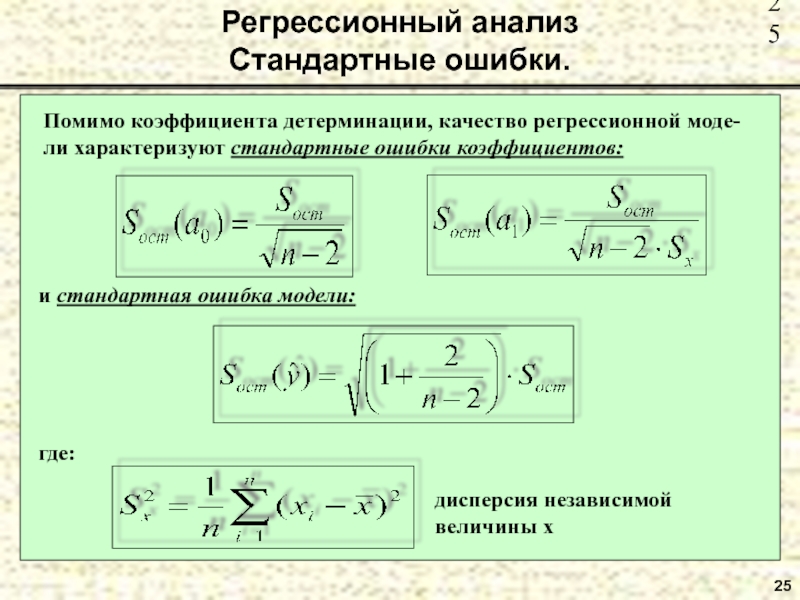
- 25. 25 Регрессионный анализ Стандартные ошибки.
- 26. 26 Регрессионный анализ Схема проверки гипотез
- 27. 27 27 Регрессионный анализ Схема проверки гипотез
- 28. 28 28 Регрессионный анализ Проверка гипотезы о
- 29. 29 29 Регрессионный анализ Проверка гипотезы о
- 30. 30 Регрессионный анализ Проверка гипотезы о значимости
- 31. 31 Регрессионный анализ Нелинейная парная регрессия
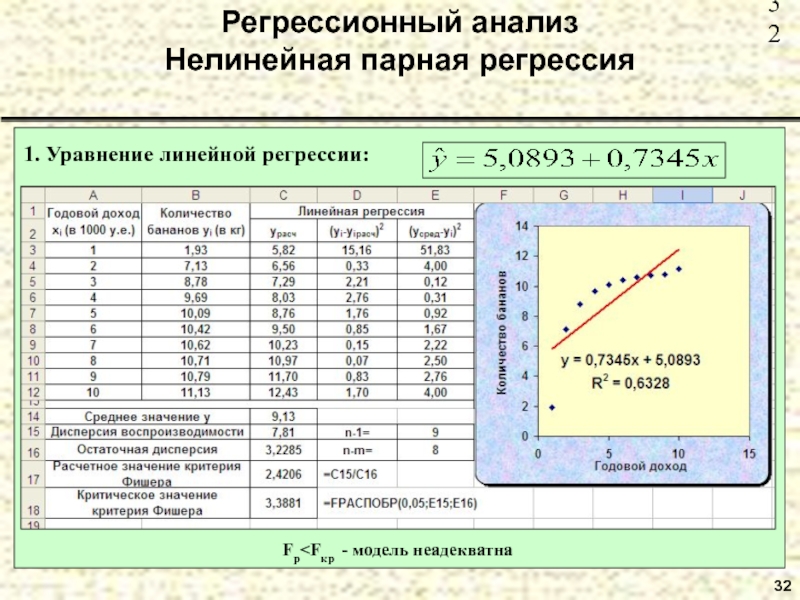
- 32. 32 Регрессионный анализ Нелинейная парная регрессия 1. Уравнение линейной регрессии: Fp
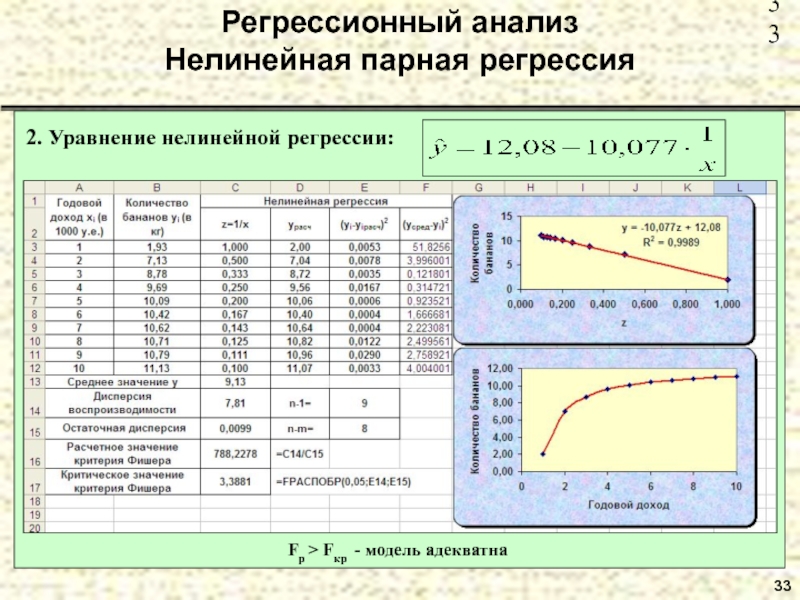
- 33. 33 Регрессионный анализ Нелинейная парная регрессия
- 34. 34 Регрессионный анализ Нелинейная парная регрессия
Слайд 1Автор: Равичев Л.В.
РХТУ им. Д.И.Менделеева
Кафедра управления технологическими инновациями
Москва - 2013
СТАТИСТИКА
Лекция
Слайд 22
Корреляционный и регрессионный анализ
Основная задача статистики – обнаружить связь между явлениями,
Вид связи между явлениями
Слайд 33
Корреляционный и регрессионный анализ
Предмет корреляционно-регрессионного анализа составляет исследова-ние статистических зависимостей между
Корреляционный анализ
Регрессионный анализ
Слайд 44
Корреляционный анализ
Диаграмма рассеяния
Простейшим приемом при исследовании зависимости между двумя коли-чественными признаками
Пример 1. Построить диаграмму рассеяния для результатов наблюдения за возрастом и артериальным давлением группы людей, приведенных в таблице.
Слайд 55
Корреляционный анализ
Линейный коэффициент корреляции Пирсона
Наиболее часто употребляемой количественной характеристикой линей-ных зависимостей
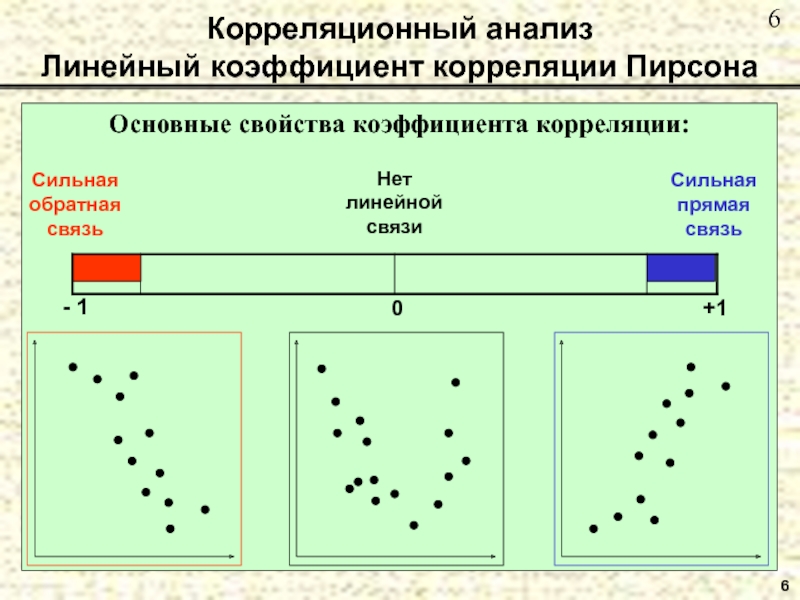
Слайд 6Корреляционный анализ
Линейный коэффициент корреляции Пирсона
Основные свойства коэффициента корреляции:
Нет линейной связи
Слайд 77
Корреляционный анализ
Линейный коэффициент корреляции Пирсона
Пример 2. Для данных, приведенных в примере
Слайд 88
Корреляционный анализ
Линейный коэффициент корреляции Пирсона
Пример 3. Для данных, приведенных в таблице
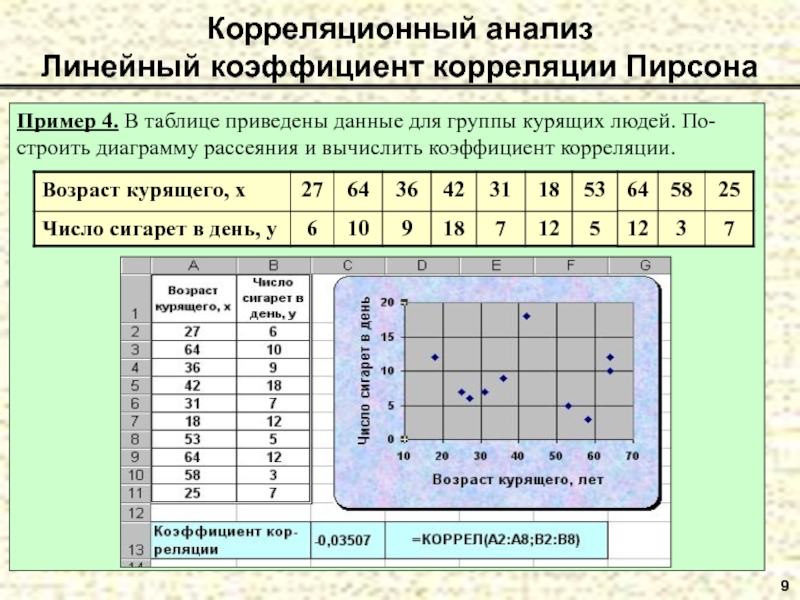
Слайд 99
Корреляционный анализ
Линейный коэффициент корреляции Пирсона
Пример 4. В таблице приведены данные для
Слайд 1010
Корреляционный анализ
Проверка значимости коэффициента корреляции
Линейный коэффициент корреляции для генеральной совокупности:
Слайд 1111
Корреляционный анализ
Проверка значимости коэффициента корреляции
Оценка значимости коэффициента корреляции проводится с помощью
Относительно генерального коэффициента корреляции можно выдвинуть две гипотезы:
генеральный коэффициент корреляции равен 0 (основная гипотеза);
генеральный коэффициент корреляции отличен от 0.
Сформировав выборку и рассчитав её коэффициент корреляции r, необходимо решить – является ли его значение настолько большим, чтобы вероятность (по различным выборкам) выпадения такого зна-чения при нулевом генеральном коэффициенте корреляции ρ была бы мала (меньше уровня значимости). Если является, то в этом слу-чае основная гипотеза отвергается, а коэффициент корреляции и ус-тановленная зависимость между величинами полагаются значимы-ми.
Слайд 1212
Корреляционный анализ
Проверка значимости коэффициента корреляции
Пример 5. Исследовать значимость коэффициента корреляции, рассчитан-ного
Слайд 1313
Корреляционный анализ
Проверка значимости коэффициента корреляции
Вывод: прямая зависимость между возрастом человека и
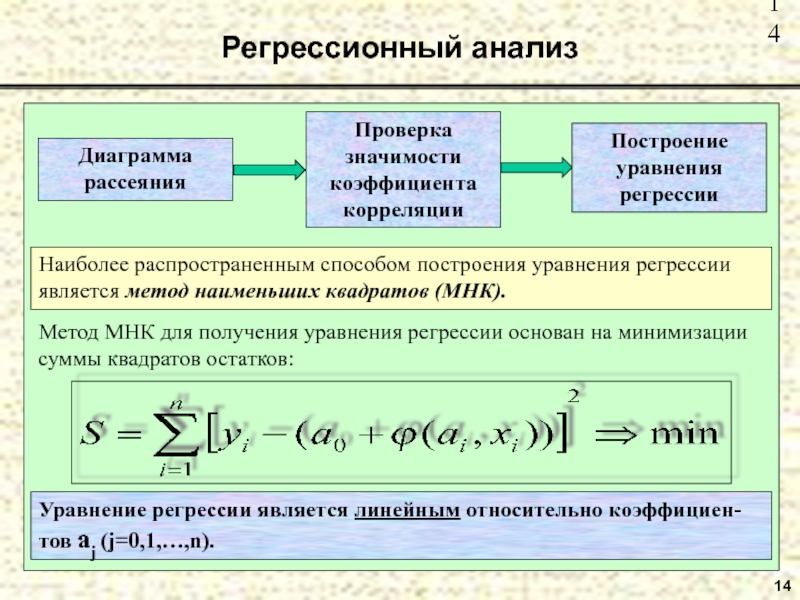
Слайд 1414
Регрессионный анализ
Диаграмма рассеяния
Наиболее распространенным способом построения уравнения регрессии является метод наименьших
Метод МНК для получения уравнения регрессии основан на минимизации суммы квадратов остатков:
Уравнение регрессии является линейным относительно коэффициен-тов aj (j=0,1,…,n).
Слайд 1818
Пример 6. Построить уравнение линейной регрессии для зависимости величин возраста и
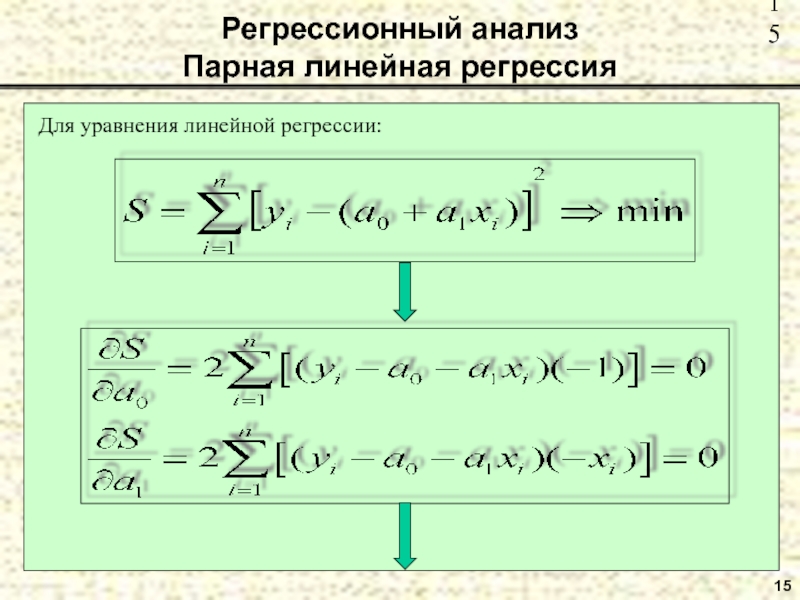
Регрессионный анализ
Парная линейная регрессия
Слайд 1919
Пример 7. Построить уравнение линейной регрессии для зависимости количества пропущенных занятий
Регрессионный анализ
Парная линейная регрессия
Слайд 2020
Пример 8. Построить уравнение линейной регрессии для данных, при-веденных в примере
Регрессионный анализ
Парная линейная регрессия
Слайд 2424
Регрессионный анализ
Анализ точности модели.
Коэффициент детерминации:
Коэффициент детерминации является основной характеристикой регрессионной модели
Одним из практических применений коэффициента детерминации является оценка качества и сравнение между собой различных мо-делей (линейной и нелинейных) парной регрессии.
Слайд 2525
Регрессионный анализ
Стандартные ошибки.
Помимо коэффициента детерминации, качество регрессионной моде-ли характеризуют стандартные ошибки
и стандартная ошибка модели:
где:
дисперсия независимой величины х
Слайд 2626
Регрессионный анализ
Схема проверки гипотез о значимости коэффициентов.
При уровне значимости 5%
Пример 9. На основании данных наблюдений в США за 25 – летний период (1959 – 1983 годы) построена зависимость суммарных расходов на питание (y) от располагаемых доходов (х):
Слайд 2727
27
Регрессионный анализ
Схема проверки гипотез о значимости коэффициентов.
1) Гипотезы для обоих коэффициентов
Н0: a0=0; H1: a0≠0.
Н0: a1=0; H1: a1≠0.
Слайд 2828
28
Регрессионный анализ
Проверка гипотезы о значимости модели.
Для решения вопроса действительно ли полученное
Слайд 2929
29
Регрессионный анализ
Проверка гипотезы о значимости модели.
Способы нахождения критерия Фишера.
1) С помощью
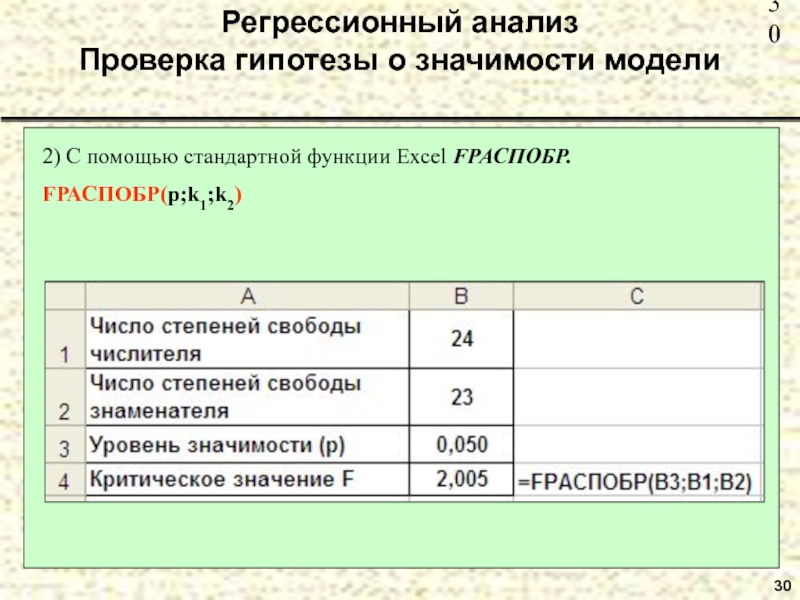
Слайд 3030
Регрессионный анализ
Проверка гипотезы о значимости модели
2) С помощью стандартной функции Excel
FРАСПОБР(p;k1;k2)
Слайд 3131
Регрессионный анализ
Нелинейная парная регрессия
Пример 10. В таблице приведены данные количества покупаемых
Построить уравнения линейной и нелинейной регрессии и оценить качество полученных моделей.