- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Угол между векторами. Скалярное произведение векторов презентация
Содержание
- 1. Угол между векторами. Скалярное произведение векторов
- 2. Ввести понятия угла между векторами и скалярного
- 3. Повторение: Какие векторы называются равными?
- 4. Повторение Векторы в пространстве. 1) Дано:
- 5. Угол между векторами.
- 6. Скалярное произведение векторов. Скалярным произведением двух
- 7. = 0 Скалярное
- 8. Скалярное произведение ненулевых векторов положительно
- 9. Скалярное произведение ненулевых векторов отрицательно
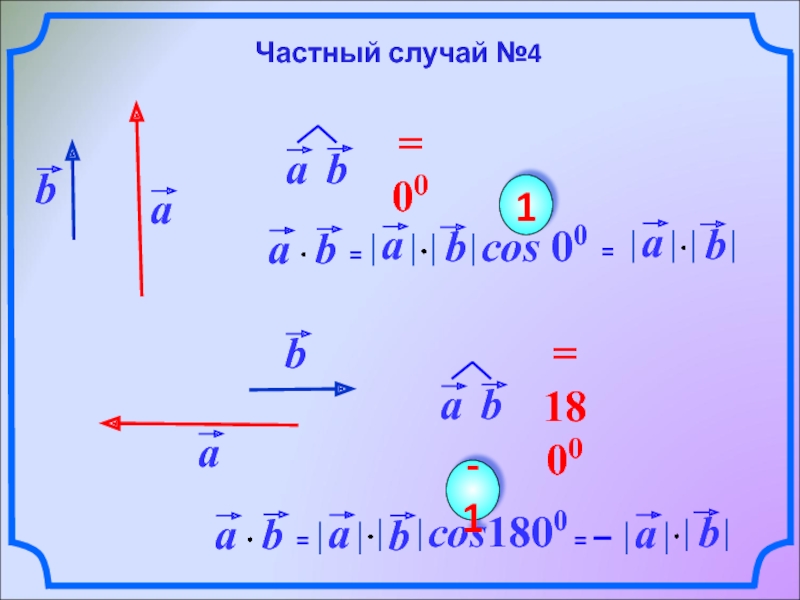
- 10. cos 00 1 cos1800 -1 Частный случай №4
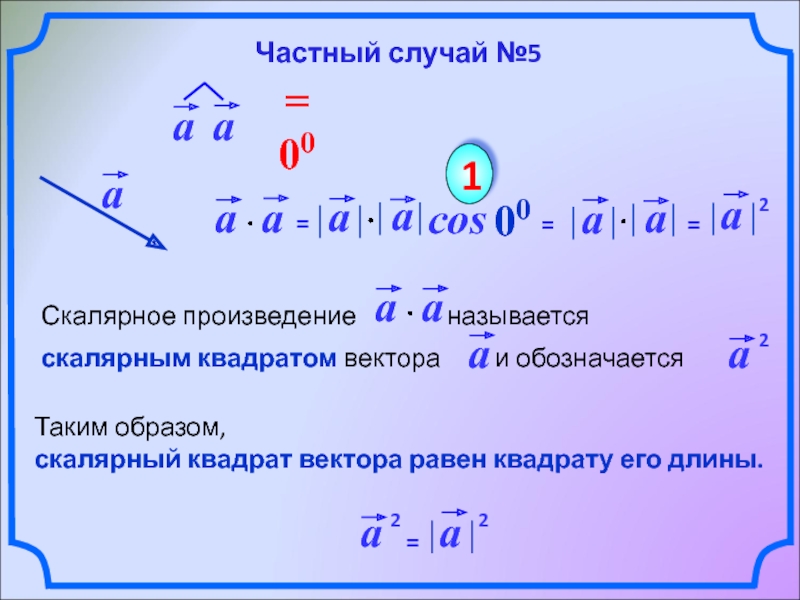
- 11. cos 00 1 Таким образом,
- 12. Пример применения скалярного произведение векторов в физике.
- 13. Все ребра тетраэдра АВСD равны друг
- 14. Формула скалярного произведения векторов в пространстве. Скалярное
- 15. Скалярное произведение векторов.
- 16. Косинус угла между ненулевыми векторами
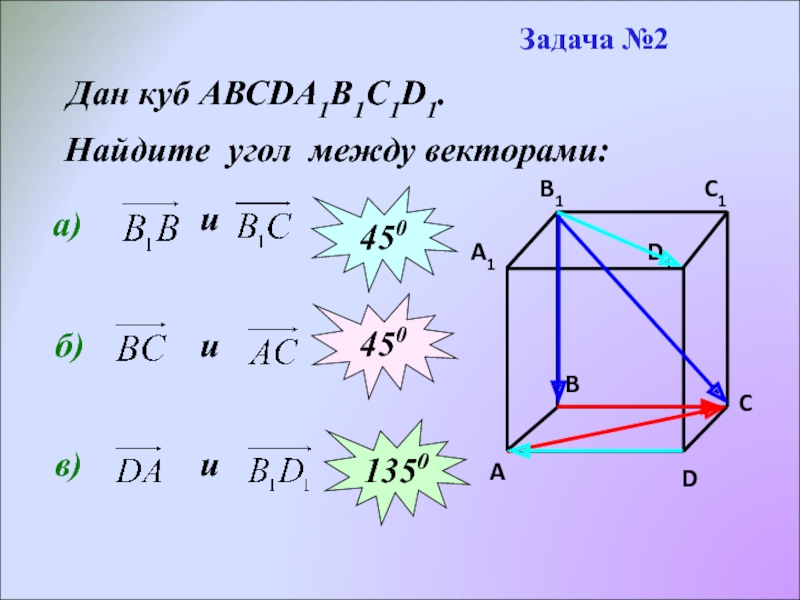
- 17. Задача №2 Найдите угол между векторами: а)
- 18. № 443 (г) Дано:
- 19. № 443 (г) Дано:
- 20. № 443 (г) Дано:
- 21. Скалярное произведение векторов.
- 22. Задание №1 Найти скалярное произведение векторов: a
- 23. Задание №2 Найти скалярное произведение векторов: a
- 24. Задание №3 Найти скалярное произведение векторов: a
- 25. Проверочная работа 1. Найти скалярное произведение векторов:
- 26. Проверочная работа 2. Найти скалярное произведение векторов:
- 27. Проверочная работа 3. Найти скалярное произведение векторов:
- 28. Проверочная работа 4. Найти скалярное произведение векторов:
- 29. Проверочная работа 5. Найти скалярное произведение векторов:
- 30. Проверочная работа Работа закончена. Перейдём к проверке.
- 31. Проверочная работа 1. Найти скалярное произведение векторов:
- 32. Проверочная работа 2. Найти скалярное произведение векторов:
- 33. Проверочная работа 3. Найти скалярное произведение векторов:
- 34. Проверочная работа 4. Найти скалярное произведение векторов:
- 35. Проверочная работа 5. Найти скалярное произведение векторов:
- 36. Домашнее задание П.50, 51 № 441, № 444, 446 (а)
Слайд 2Ввести понятия угла между векторами и скалярного произведения векторов.
Рассмотреть формулу скалярного
Показать применение скалярного произведения векторов при решении задач.
Цели урока:
Слайд 3Повторение:
Какие векторы называются равными?
Как найти длину вектора по координатам его начала
А
В
Какие векторы являются коллинеарными?
или
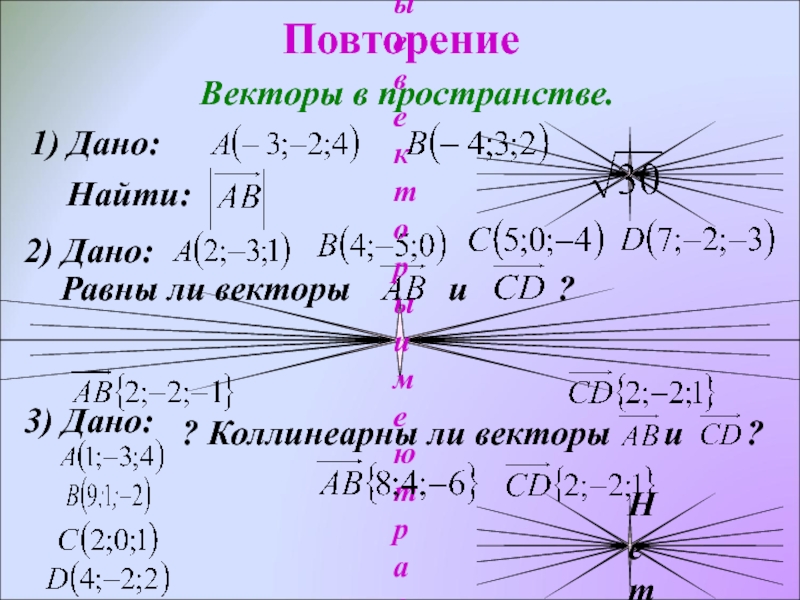
Слайд 4Повторение
Векторы в пространстве.
1) Дано:
Найти:
2) Дано:
Равны ли векторы
Нет, т.к.равные векторы имеют равные
координаты.
3) Дано:
? Коллинеарны ли векторы и ?
Нет
Слайд 6Скалярное произведение векторов.
Скалярным произведением
двух векторов называется
произведение их длин
на косинус угла
ними.
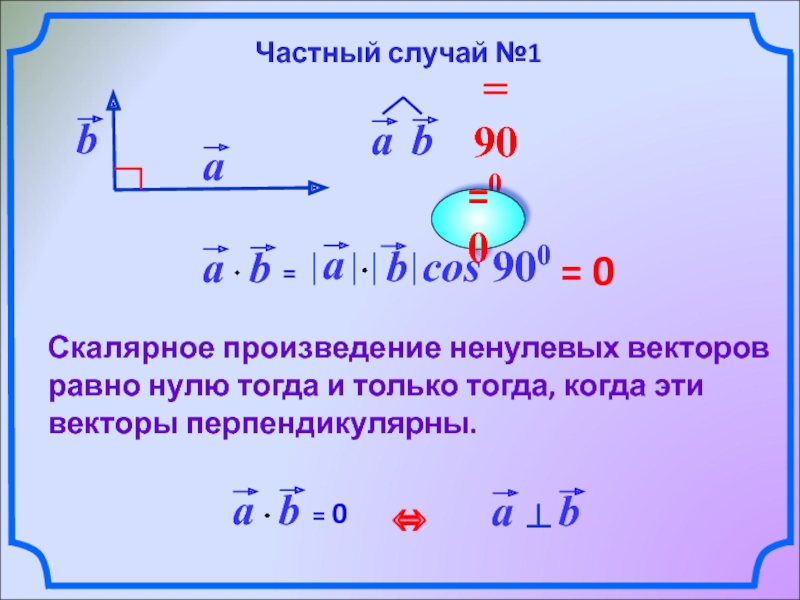
Слайд 7
= 0
Скалярное произведение ненулевых векторов равно нулю тогда и только
Частный случай №1
= 0
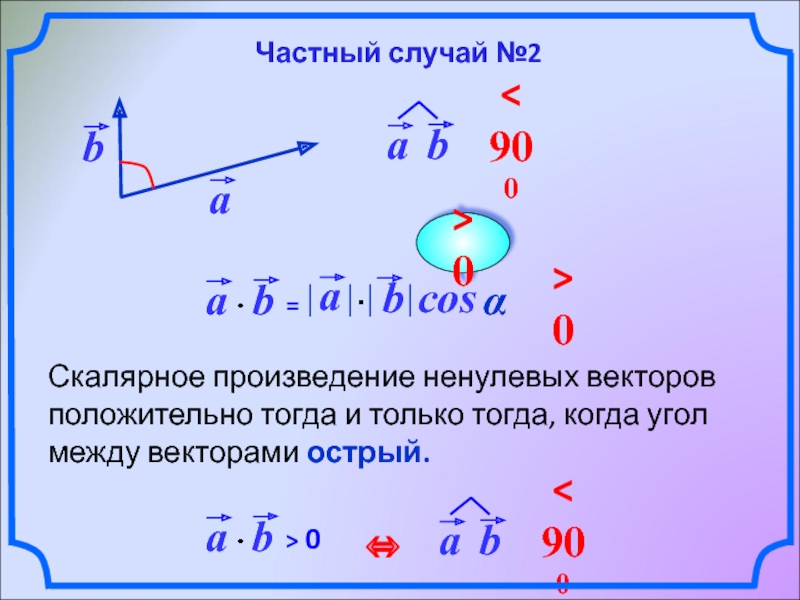
Слайд 8
Скалярное произведение ненулевых векторов положительно тогда и только тогда, когда угол
cos
α
> 0
> 0
Частный случай №2
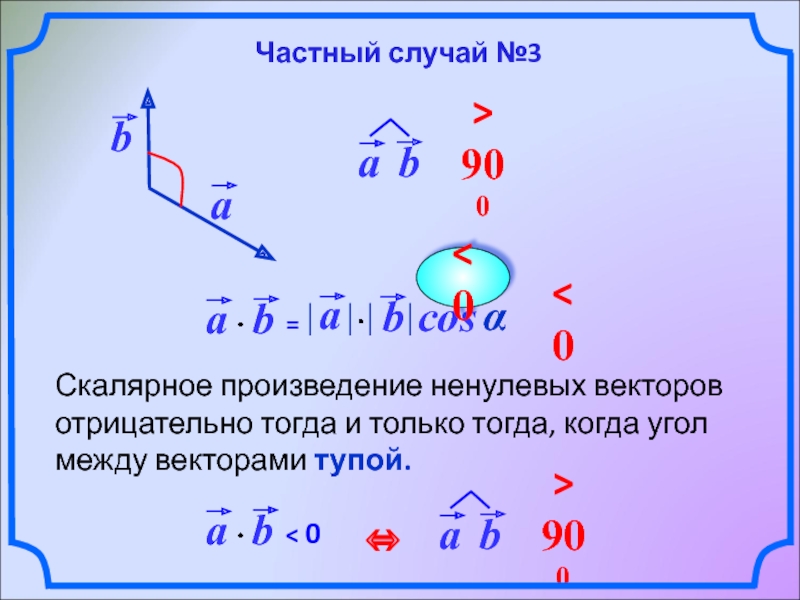
Слайд 9
Скалярное произведение ненулевых векторов отрицательно тогда и только тогда, когда угол
cos
α
< 0
< 0
Частный случай №3
Слайд 11cos
00
1
Таким образом,
скалярный квадрат вектора равен квадрату его длины.
Частный случай №5
2
2
2
2
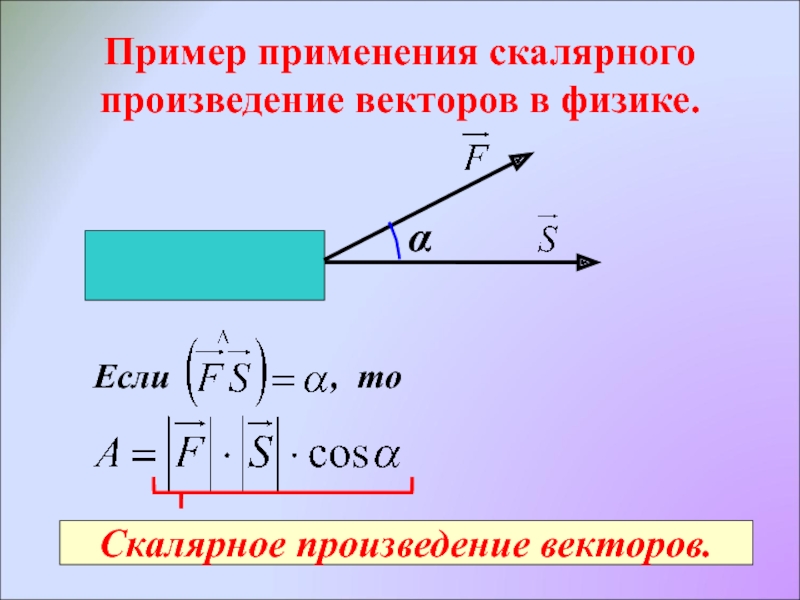
Слайд 12Пример применения скалярного произведение векторов в физике.
α
Если
Скалярное произведение векторов.
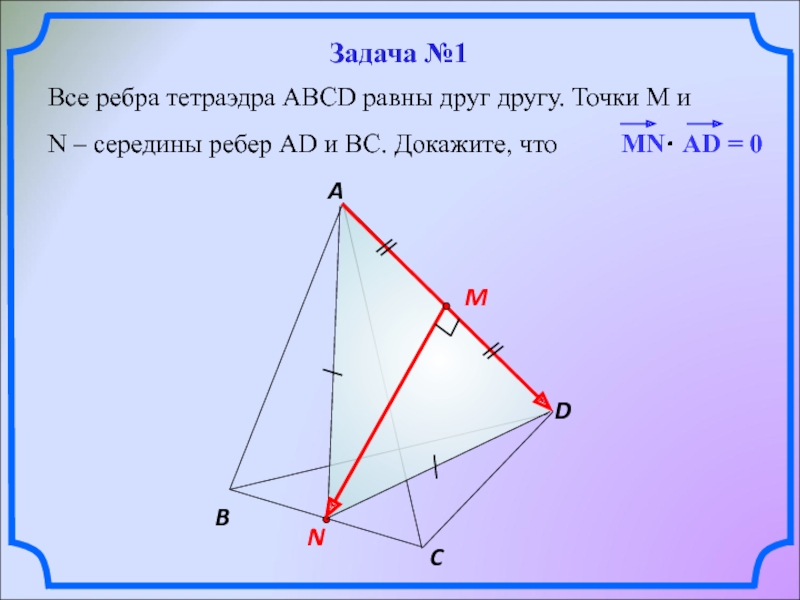
Слайд 13 Все ребра тетраэдра АВСD равны друг другу. Точки М и
B
C
N
A
D
M
Задача №1
Слайд 14Формула скалярного произведения векторов в пространстве.
Скалярное произведение двух векторов равно сумме
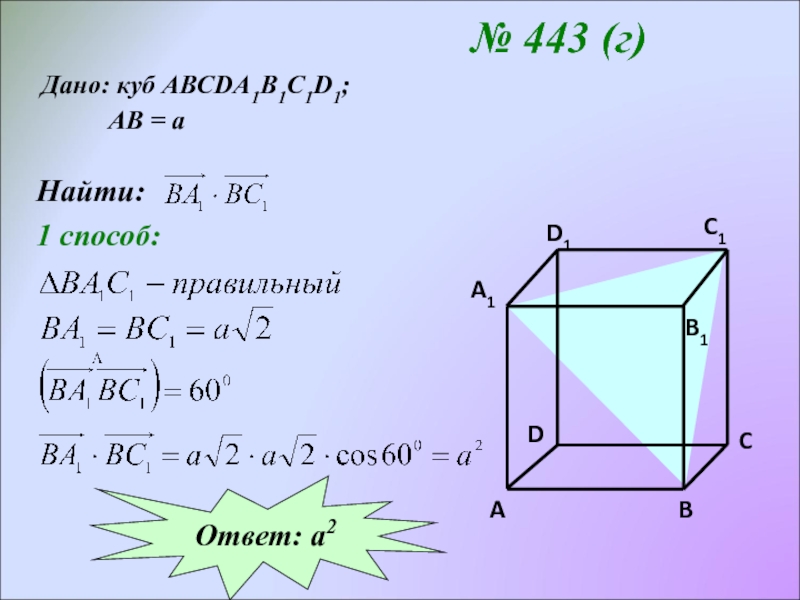
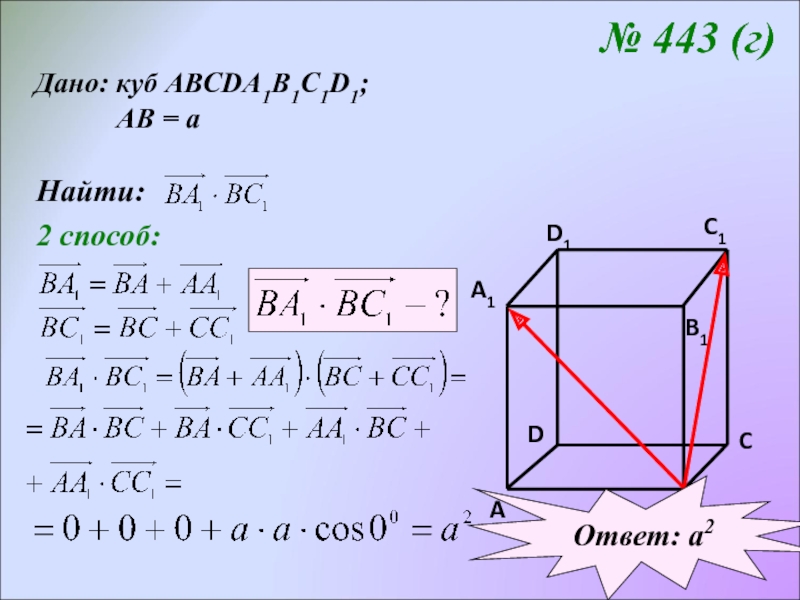
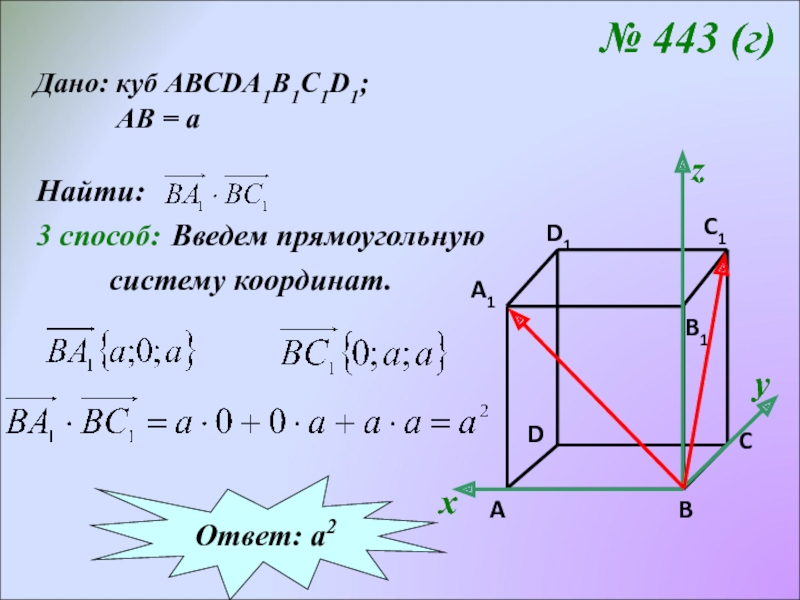
Слайд 20№ 443 (г)
Дано: куб АВСDA1B1C1D1;
Найти:
3 способ:
Введем прямоугольную
систему координат.
х
у
z
Ответ: а2
Слайд 22Задание №1
Найти скалярное произведение векторов:
a {-6; 9; 5}
b {-1; 0; 7}
x1x2
-6 (-1) + 9 0 + 5 7 = 41
Слайд 23Задание №2
Найти скалярное произведение векторов:
a {0; 0; 4}
b {22; 1; 8}
x1x2
0 22 + 0 1 + 4 8 = 32
Слайд 24Задание №3
Найти скалярное произведение векторов:
a {1; 7; 9}
b {-2; 4; 0}
x1x2
1 (-2) + 7 4 + 9 0 = 26
Слайд 31Проверочная работа
1. Найти скалярное произведение векторов:
a {1; 10; 7}
b {0; 7;
10 7 = 70
Слайд 32Проверочная работа
2. Найти скалярное произведение векторов:
a {7; 25; 0}
b {11; 0;
7 11 = 77
Слайд 33Проверочная работа
3. Найти скалярное произведение векторов:
a {|-2|; 0; |3|}
b {1; |-11|;
2 1 + 3 1 = 5
Слайд 34Проверочная работа
4. Найти скалярное произведение векторов:
a {sin(900); 2; 3}
b {3; 2;
1 3 + 2 2 + 3 1 = 10
Слайд 35Проверочная работа
5. Найти скалярное произведение векторов:
a {-1; 2; 8}
b {5; 5;
-1 5 + 2 5 = 5