- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Построение сечений многогранников презентация
Содержание
- 1. Построение сечений многогранников
- 2. Определение сечения.
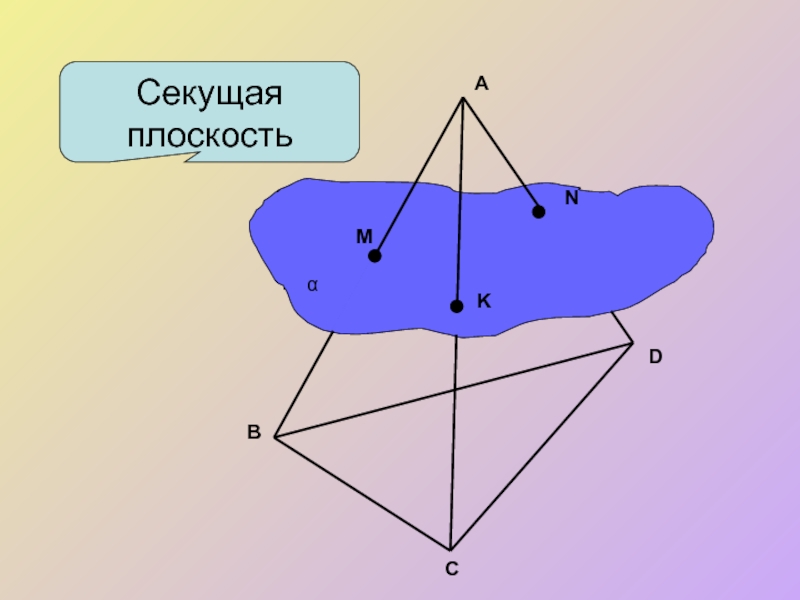
- 3. Секущая плоскость А В С D M N K α
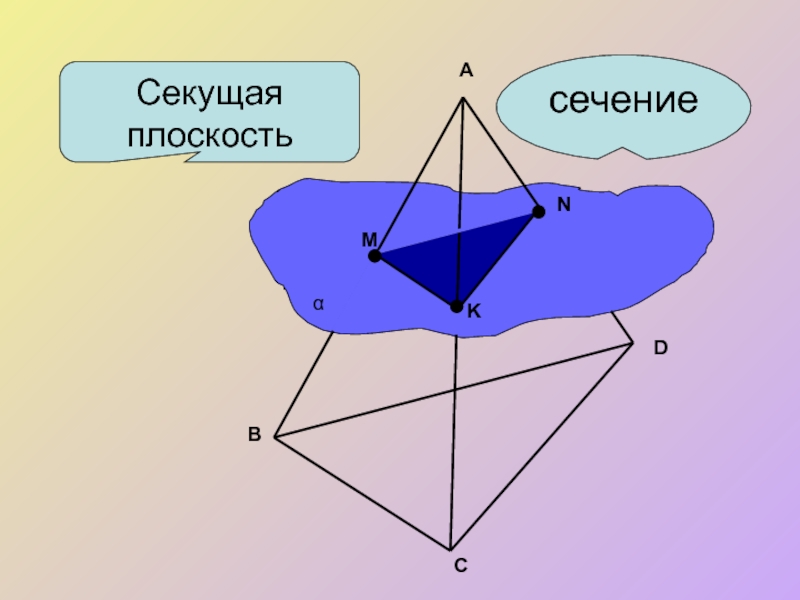
- 4. Секущая плоскость
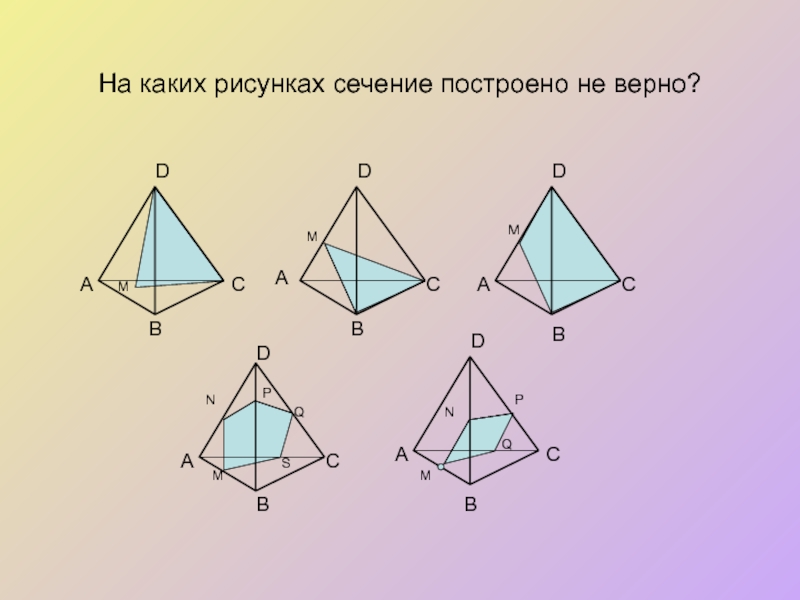
- 5. На каких
- 6. P N Построить сечение тетраэдра
- 7. Построить сечение тетраэдра плоскостью, заданной тремя точками.
- 8. Построить сечение тетраэдра
- 9. Аксиоматический метод
- 10. Постройте сечение пирамиды плоскостью, проходящей
- 11. XY – след секущей плоскости
- 12. Практическая работа. Постройте сечение многогранника плоскостью, проходящей
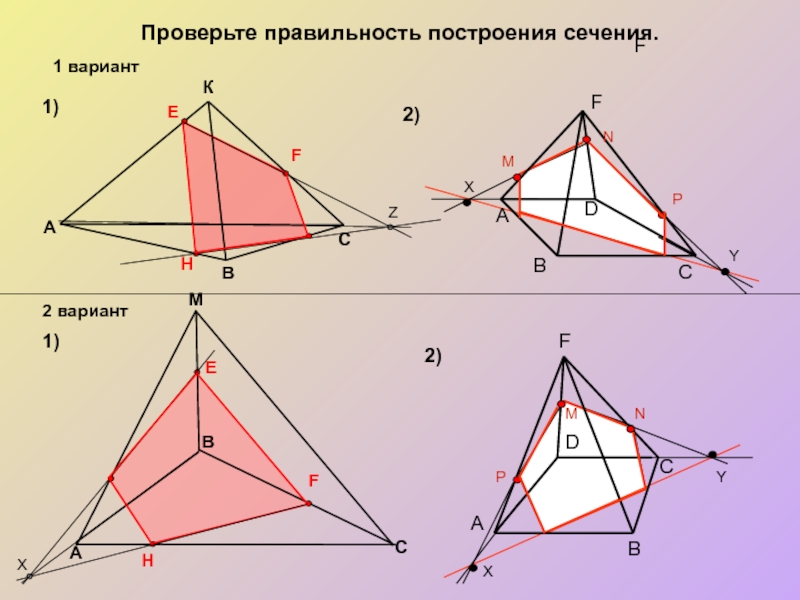
- 13. Проверьте правильность построения
- 14. Домашнее задание: § 4. п.14. учебника
Слайд 1
Построение сечений многогранников
Презентация выполнена
учителем математики
МОУ лицея № 28 имени
Слайд 2
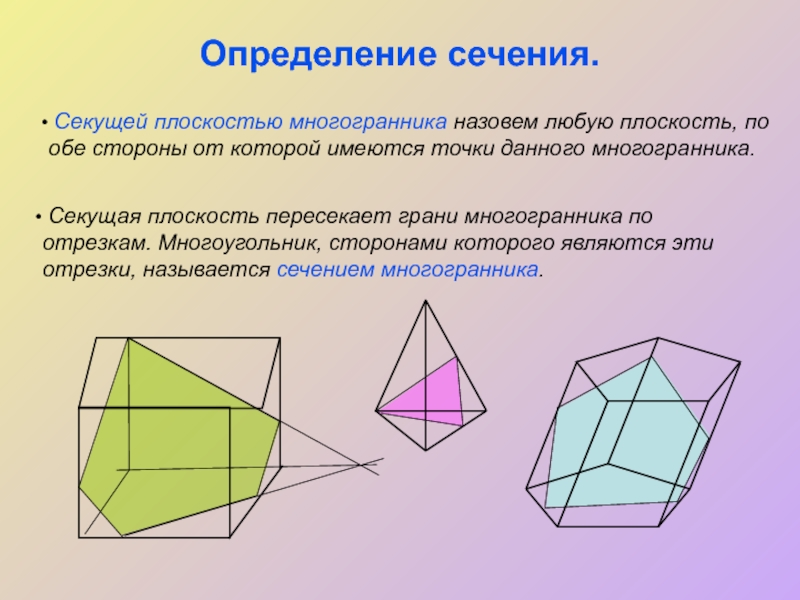
Определение сечения.
Секущей плоскостью многогранника назовем любую плоскость, по обе стороны
Секущая плоскость пересекает грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.
Слайд 6
P
N
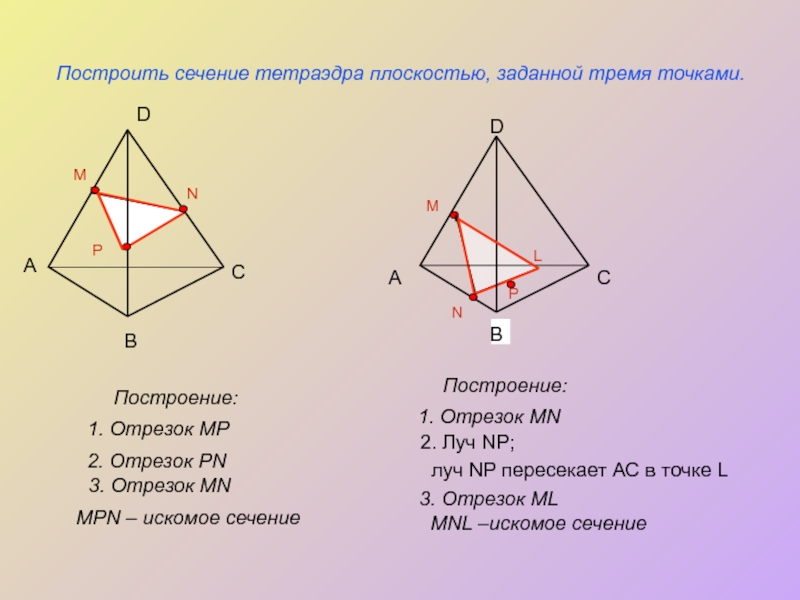
Построить сечение тетраэдра плоскостью, заданной тремя точками.
Построение:
А
В
С
D
P
M
N
2.
А
В
С
D
M
L
1. Отрезок MP
Построение:
3. Отрезок MN
MPN – искомое сечение
1. Отрезок MN
2. Луч NP;
луч NP пересекает АС в точке L
3. Отрезок ML
MNL –искомое сечение
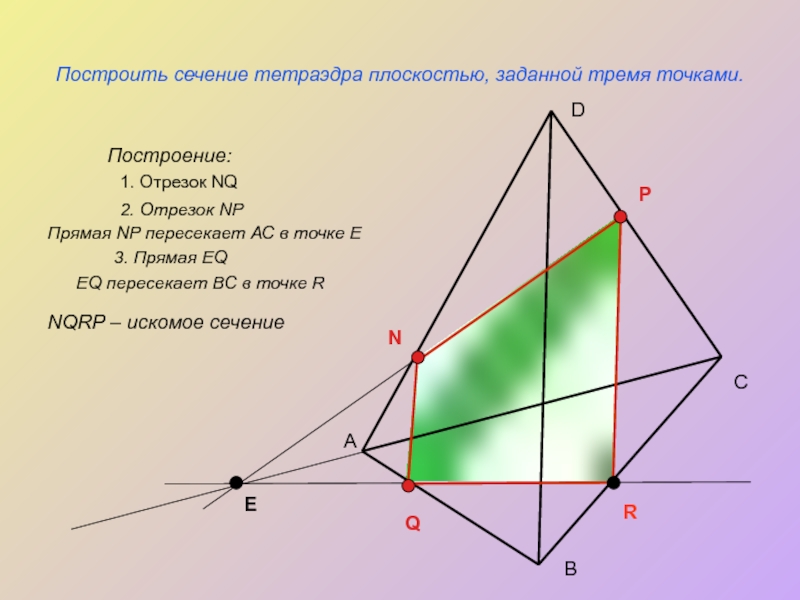
Слайд 7Построить сечение тетраэдра плоскостью, заданной тремя точками.
Построение:
А
С
В
D
N
P
Q
R
E
1. Отрезок NQ
2. Отрезок NP
Прямая NP пересекает АС в точке Е
3. Прямая EQ
EQ пересекает BC в точке R
NQRP – искомое сечение
Слайд 8
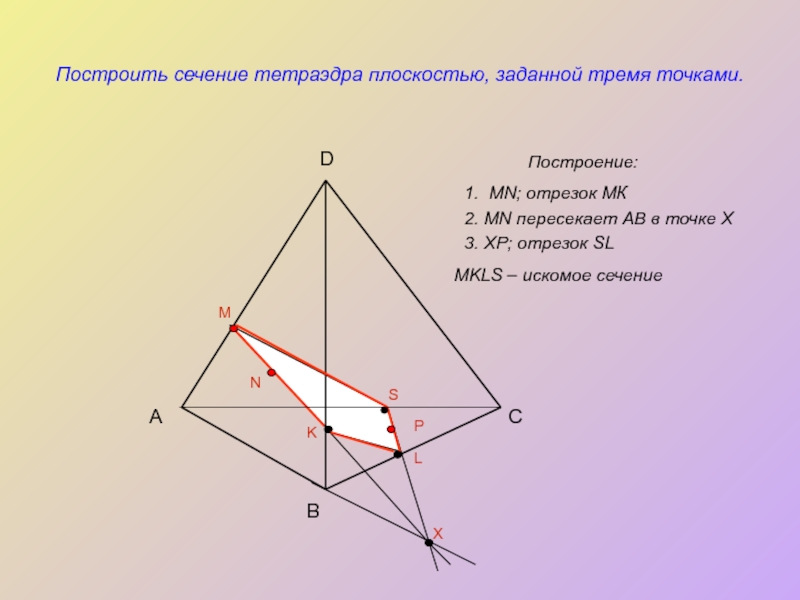
Построить сечение тетраэдра плоскостью, заданной тремя точками.
Построение:
А
B
C
D
M
N
P
X
K
S
L
1. MN; отрезок МК
2. MN
3. ХР; отрезок SL
MKLS – искомое сечение
Слайд 9 Аксиоматический метод
Метод следов
Суть метода заключается в построении
Слайд 10
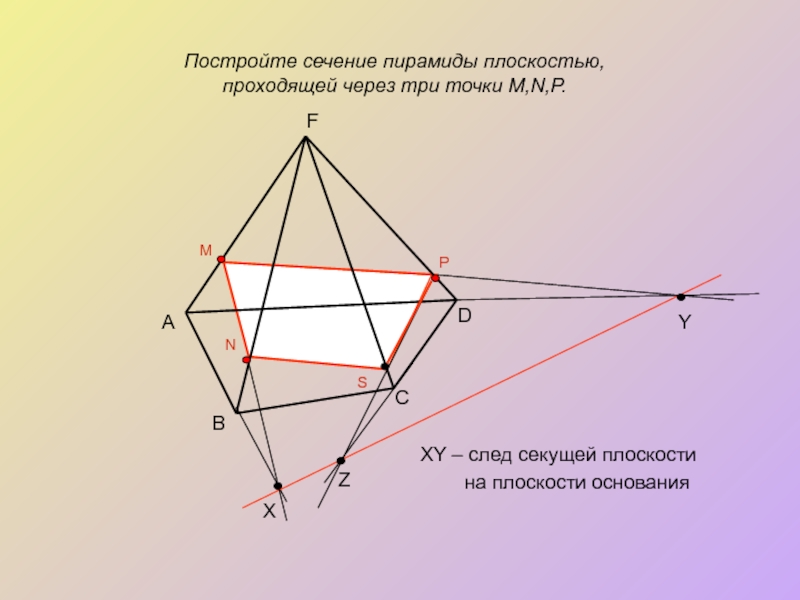
Постройте сечение пирамиды плоскостью,
проходящей через три точки M,N,P.
XY – след
на плоскости основания
D
C
B
А
Z
Y
X
M
N
P
S
F
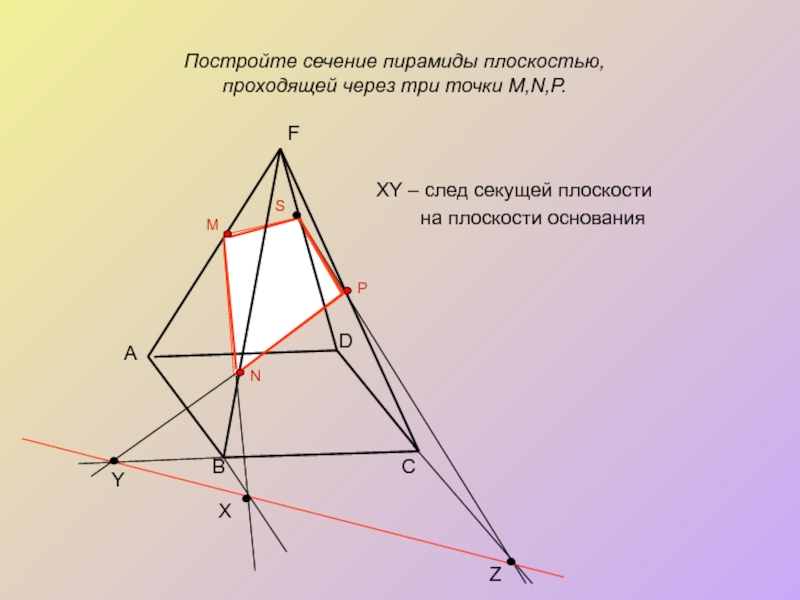
Слайд 11
XY – след секущей плоскости
на плоскости
D
C
B
Z
Y
X
M
N
P
S
Постройте сечение пирамиды плоскостью,
проходящей через три точки M,N,P.
А
F
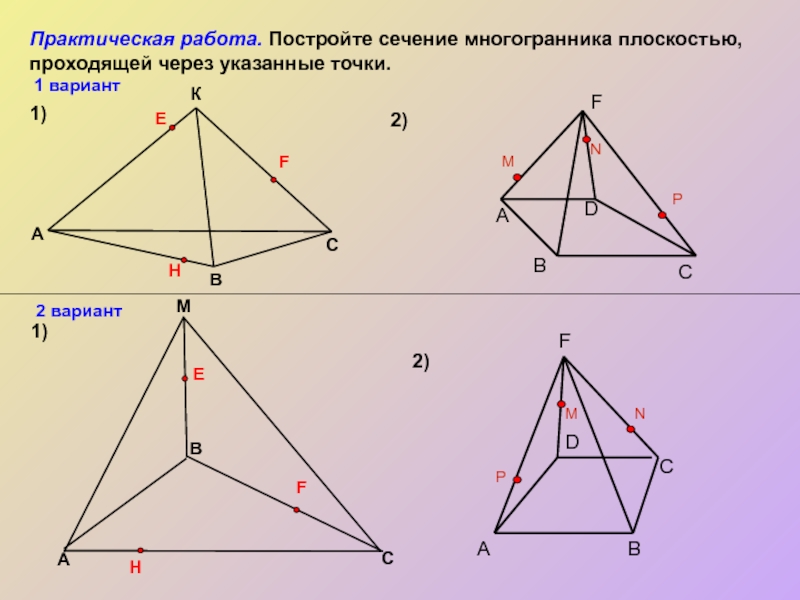
Слайд 12Практическая работа. Постройте сечение многогранника плоскостью, проходящей через указанные точки.
M
A
1)
1)
2)
2)
В
С
К
В
A
С
E
F
H
E
H
F
1 вариант
2
D
C
B
M
N
P
А
F
D
C
B
M
N
P
А
F