- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тригонометрические функции y = sin x и y = cos x . Их свойства и графики презентация
Содержание
- 1. Тригонометрические функции y = sin x и y = cos x . Их свойства и графики
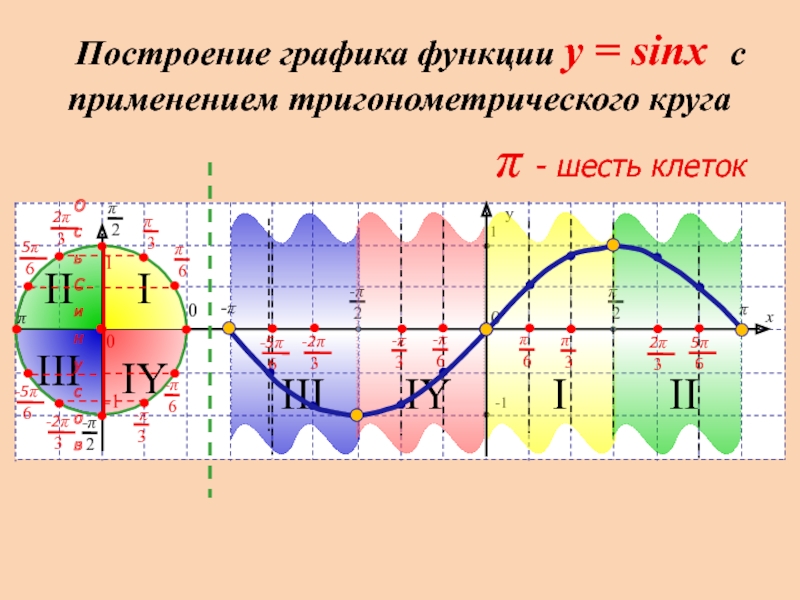
- 2. III II I IY
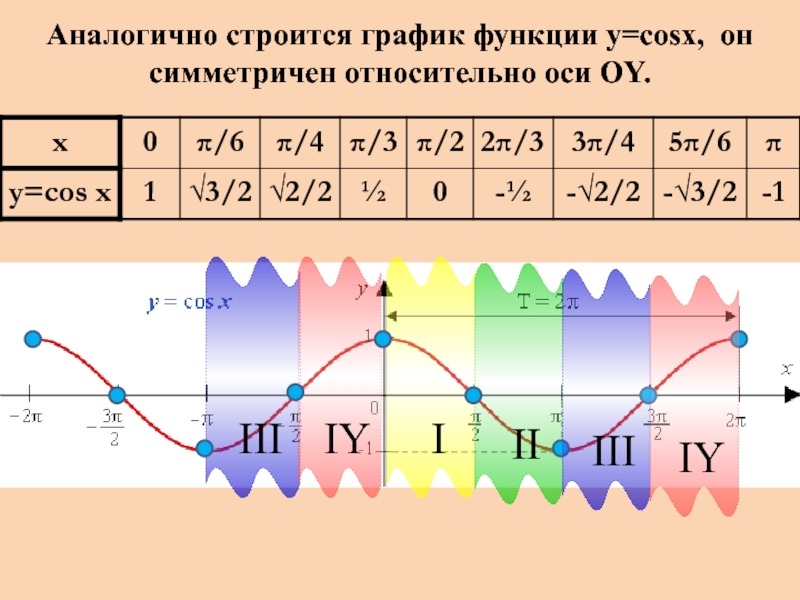
- 3. Аналогично строится график функции y=cosx, он симметричен
- 4. Свойства функции y = cos x Область
- 5. Свойства функции y = cos x (продолжение)
- 6. Свойства функции y = sin x Область
- 7. Свойства функции y = sin x (продолжение)
- 8. ПРЕОБРАЗОВАНИЕ ГРАФИКОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ. ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ
- 13. y x
- 15. y x 1 -1 -1 Какие свойства еще изменились?
- 17. y x 1 -1 2
Слайд 2III
II
I
IY
III
IY
I
II
π - шесть клеток
О
с
ь
С
и
н
у
с
о
в
Построение графика функции y
= sinx с применением тригонометрического круга
Слайд 4Свойства функции y = cos x
Область определения: D(f): х ∈ R;
Множество
значений: у ∈ [-1;1];
Периодичность: Т = 2π;
Четность: четная, т.к. cos(-x) = cos x, график симметричен относительно оси ординат;
Функция возрастает при: π+2πn ≤ x ≤ 2π(n+1), n∈Z;
Функция убывает при: πn ≤ x ≤ π + 2πn, n ∈ Z.
Периодичность: Т = 2π;
Четность: четная, т.к. cos(-x) = cos x, график симметричен относительно оси ординат;
Функция возрастает при: π+2πn ≤ x ≤ 2π(n+1), n∈Z;
Функция убывает при: πn ≤ x ≤ π + 2πn, n ∈ Z.
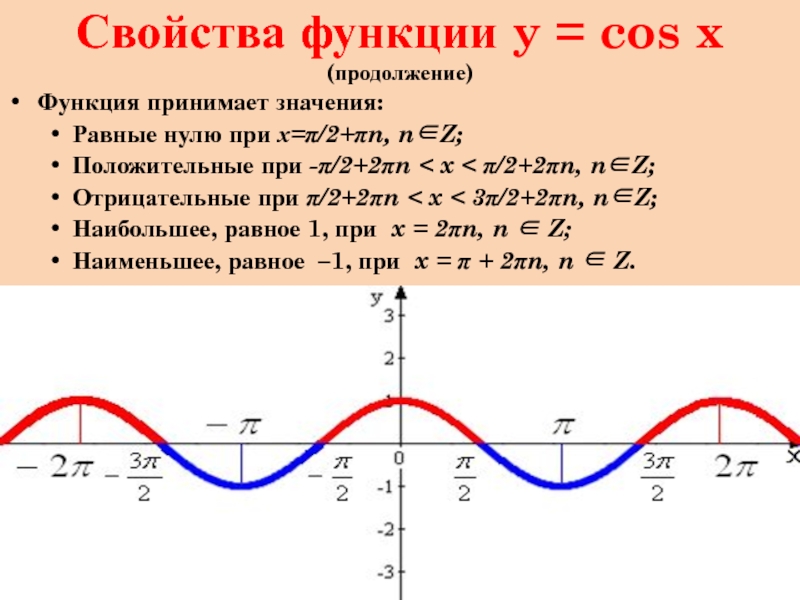
Слайд 5Свойства функции y = cos x (продолжение)
Функция принимает значения:
Равные нулю при
х=π/2+πn, n∈Z;
Положительные при -π/2+2πn < x < π/2+2πn, n∈Z;
Отрицательные при π/2+2πn < x < 3π/2+2πn, n∈Z;
Наибольшее, равное 1, при x = 2πn, n ∈ Z;
Наименьшее, равное –1, при x = π + 2πn, n ∈ Z.
Положительные при -π/2+2πn < x < π/2+2πn, n∈Z;
Отрицательные при π/2+2πn < x < 3π/2+2πn, n∈Z;
Наибольшее, равное 1, при x = 2πn, n ∈ Z;
Наименьшее, равное –1, при x = π + 2πn, n ∈ Z.
Слайд 6Свойства функции y = sin x
Область определения: D(f): х ∈ R;
Множество
значений: у ∈ [-1;1];
Периодичность: Т = 2π;
Четность: НЕчетная, т.к. sin(-x) = - sinx, график симметричен относительно начала координат;
Функция возрастает при: -π/2+2πk ≤ x ≤ π/2+2πk, k∈Z;
Функция убывает при: π/2+2πk ≤ x ≤ 3π /2 + 2π k, k ∈ Z.
Периодичность: Т = 2π;
Четность: НЕчетная, т.к. sin(-x) = - sinx, график симметричен относительно начала координат;
Функция возрастает при: -π/2+2πk ≤ x ≤ π/2+2πk, k∈Z;
Функция убывает при: π/2+2πk ≤ x ≤ 3π /2 + 2π k, k ∈ Z.
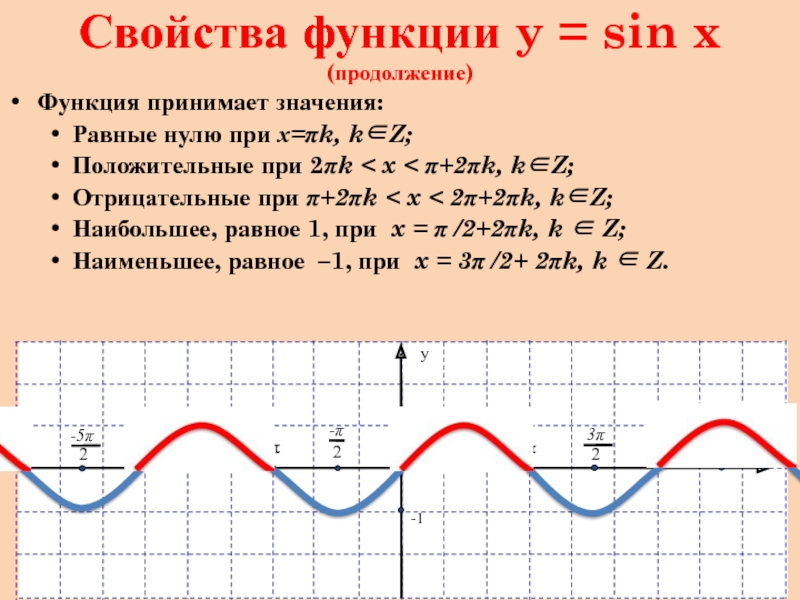
Слайд 7Свойства функции y = sin x (продолжение)
Функция принимает значения:
Равные нулю при
х=πk, k∈Z;
Положительные при 2πk < x < π+2πk, k∈Z;
Отрицательные при π+2πk < x < 2π+2πk, k∈Z;
Наибольшее, равное 1, при x = π /2+2πk, k ∈ Z;
Наименьшее, равное –1, при x = 3π /2+ 2πk, k ∈ Z.
Положительные при 2πk < x < π+2πk, k∈Z;
Отрицательные при π+2πk < x < 2π+2πk, k∈Z;
Наибольшее, равное 1, при x = π /2+2πk, k ∈ Z;
Наименьшее, равное –1, при x = 3π /2+ 2πk, k ∈ Z.
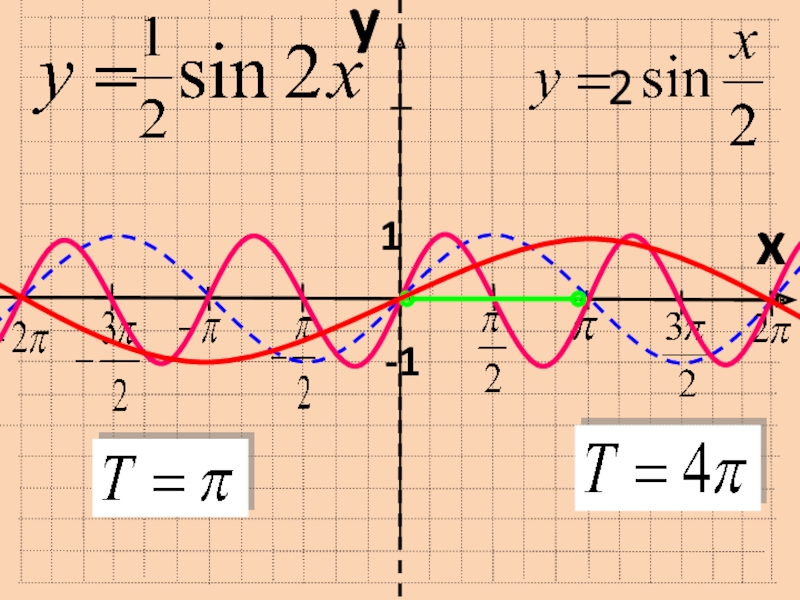
Слайд 8ПРЕОБРАЗОВАНИЕ ГРАФИКОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ.
ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ
у = sinx + m
y=
sin(x+t)
y=f(kx)
y=kf(x)
y=f(kx)
y=kf(x)
Слайд 9
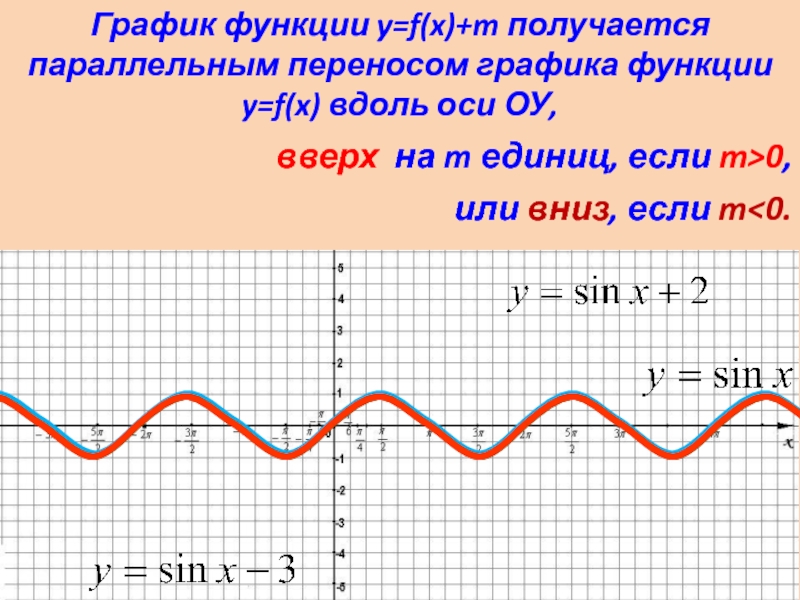
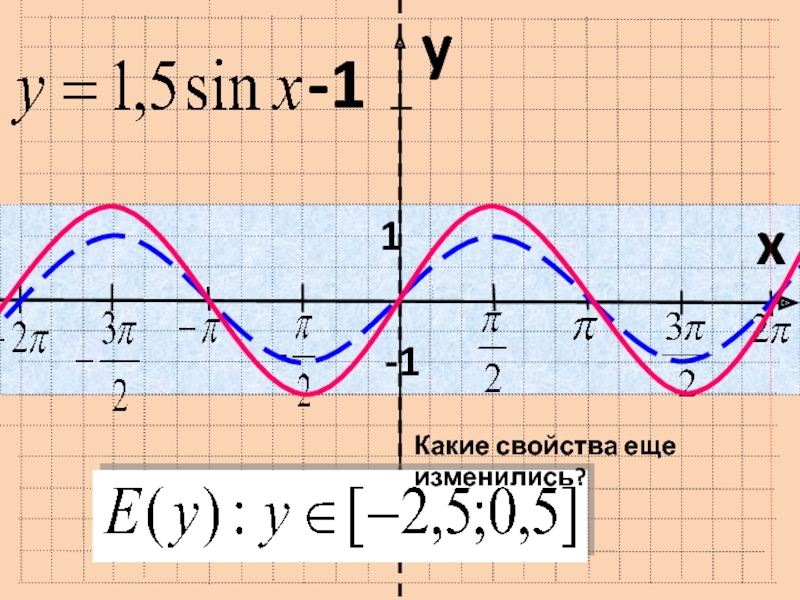
График функции y=f(x)+m получается параллельным
переносом графика функции y=f(x) вдоль оси ОУ,
вверх на m единиц, если m>0,
или вниз, если m<0.
вверх на m единиц, если m>0,
или вниз, если m<0.
Слайд 10
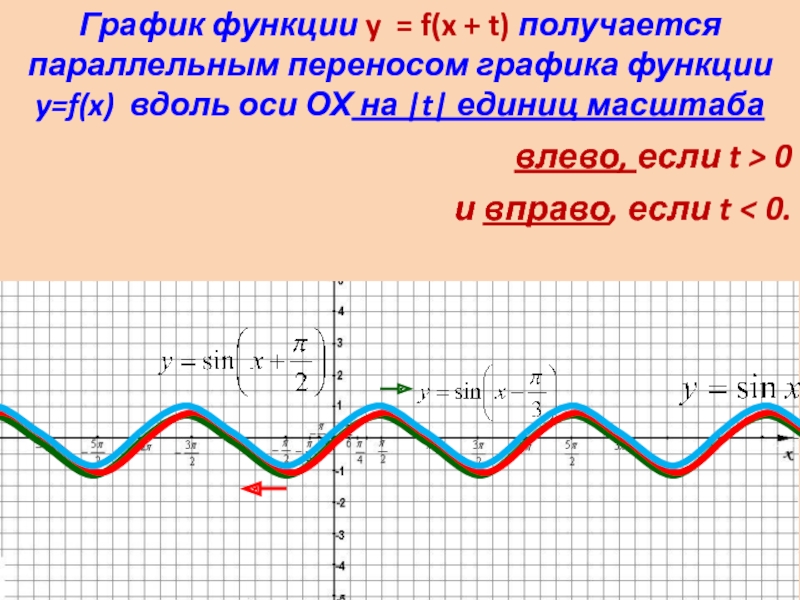
График функции y = f(x
+ t) получается параллельным переносом графика функции y=f(x) вдоль оси ОХ на |t| единиц масштаба
влево, если t > 0
и вправо, если t < 0.
влево, если t > 0
и вправо, если t < 0.
Слайд 11
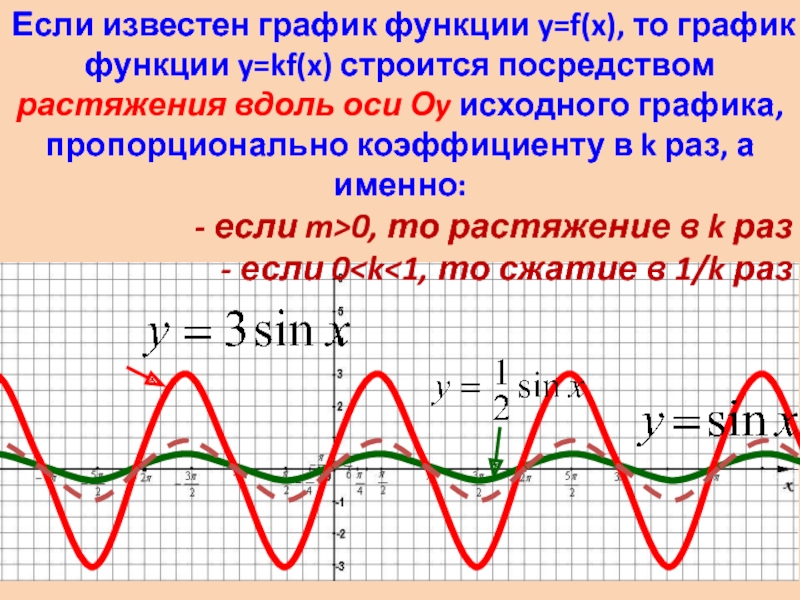
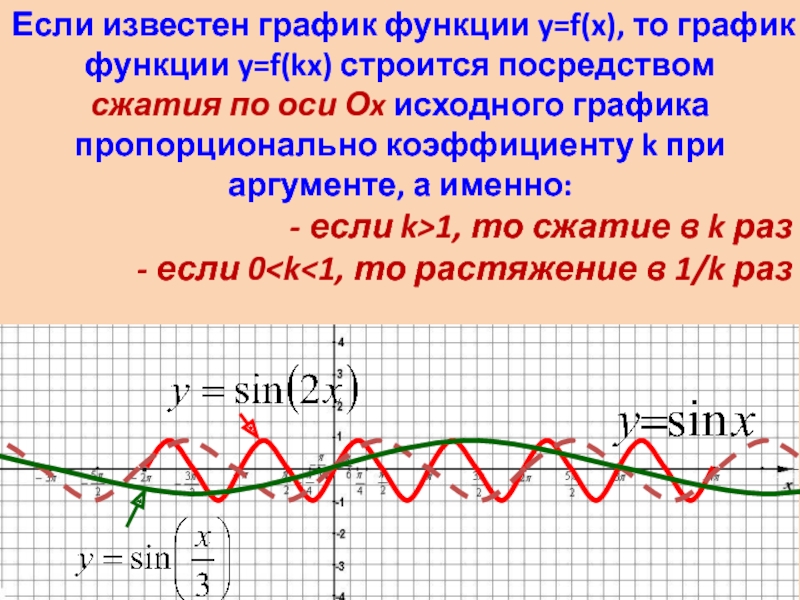
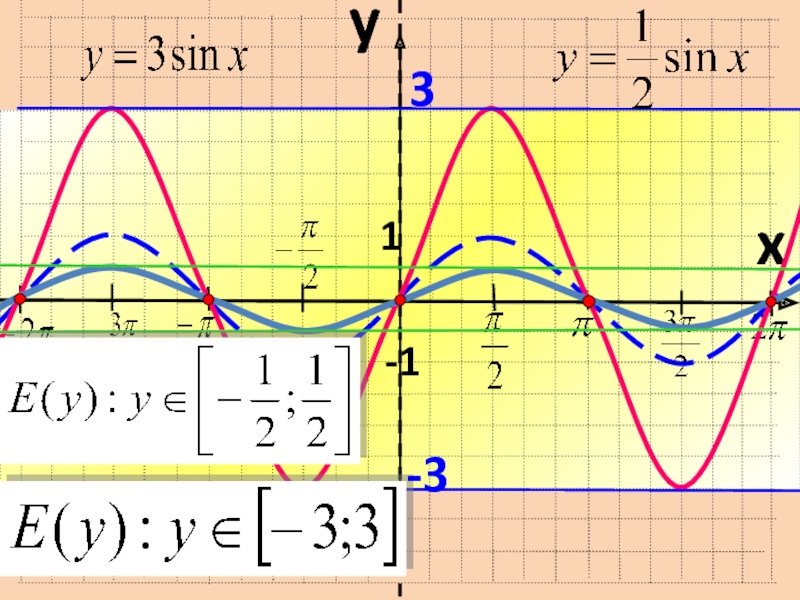
Если известен график функции y=f(x),
то график функции y=kf(x) строится посредством растяжения вдоль оси Оy исходного графика, пропорционально коэффициенту в k раз, а именно:
- если m>0, то растяжение в k раз
- если 0
- если m>0, то растяжение в k раз
- если 0
Слайд 12
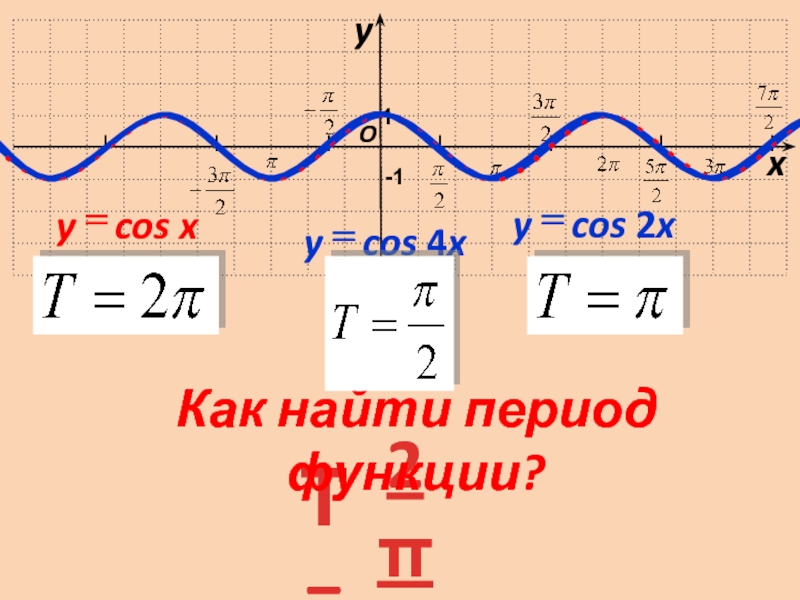
Если известен график функции y=f(x),
то график функции y=f(kx) строится посредством
сжатия по оси Оx исходного графика пропорционально коэффициенту k при аргументе, а именно:
- если k>1, то сжатие в k раз
- если 0
сжатия по оси Оx исходного графика пропорционально коэффициенту k при аргументе, а именно:
- если k>1, то сжатие в k раз
- если 0

![Свойства функции y = cos xОбласть определения: D(f): х ∈ R;Множество значений: у ∈ [-1;1];Периодичность:](/img/tmb/3/216039/94266e3cca6971fba9addc1681a02284-800x.jpg)
![Свойства функции y = sin xОбласть определения: D(f): х ∈ R;Множество значений: у ∈ [-1;1];Периодичность:](/img/tmb/3/216039/8f51c7f5594b551346a09c5a9599c888-800x.jpg)