- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Показатели вариации презентация
Содержание
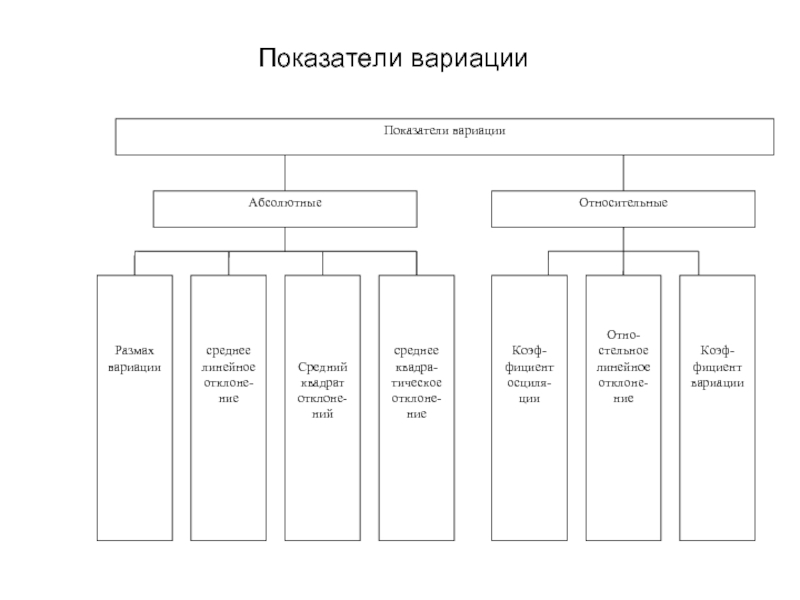
- 1. Показатели вариации
- 2. Показатели вариации (абсолютные) 1. Размах вариации
- 3. Показатели вариации (относительные) Коэффициент осцилляции:
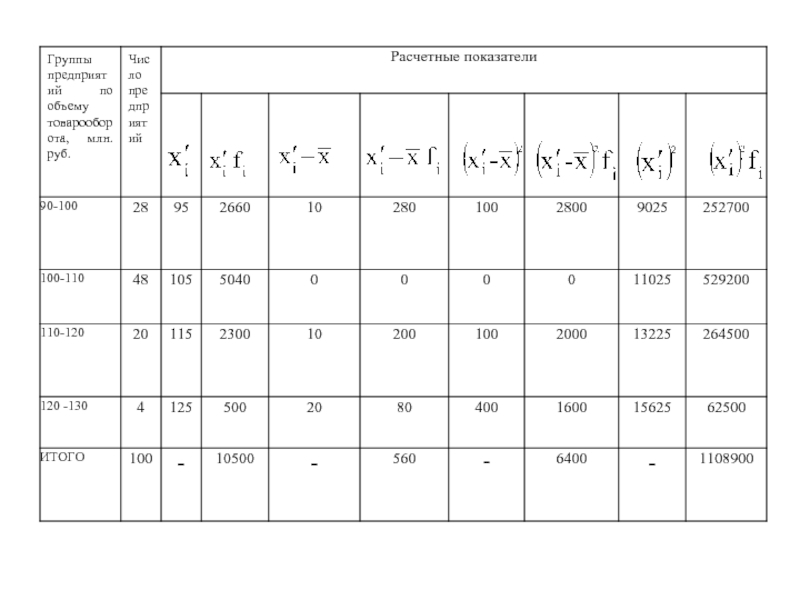
- 5. Решение примера 1 Средний объем товарооборота на
- 6. Виды дисперсий дисперсия признака по
- 7. Свойства дисперсии Общая дисперсия равна сумме средней
- 8. Продолжение решения примера 1
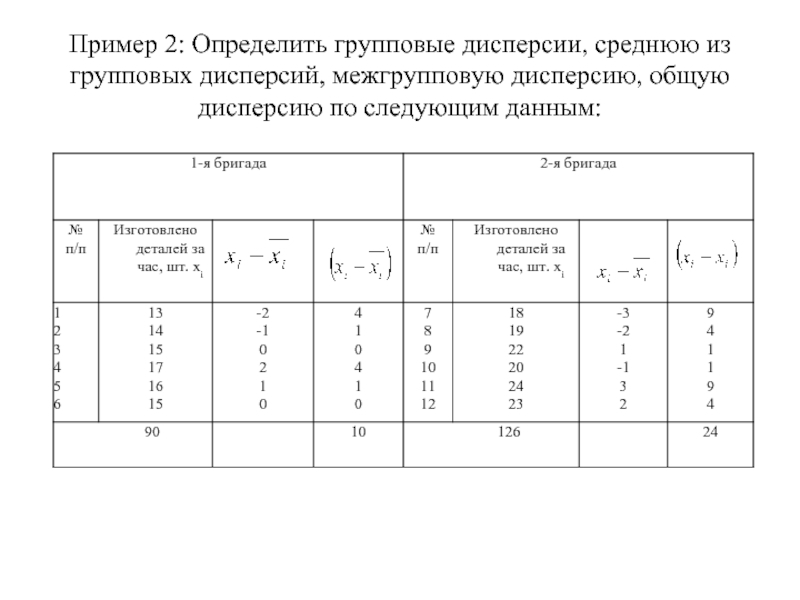
- 9. Пример 2: Определить групповые дисперсии, среднюю из
- 10. Решение: Для расчета групповых дисперсий вычислим средние
Слайд 2Показатели вариации (абсолютные)
1. Размах вариации
R = Xmax − Xmin
2. Среднее линейное отклонение
, или
, или
3. Дисперсия или средний квадрат отклонений
4. Среднее квадратическое отклонение:
Слайд 3Показатели вариации (относительные)
Коэффициент осцилляции:
Относительное линейное отклонение:
Коэффициент вариации:
Слайд 5Решение примера 1
Средний объем товарооборота на одно предприятие равен:
R = 130
млн. руб.
млн. руб.
млн. руб.
Слайд 6Виды дисперсий
дисперсия признака по всей изучаемой совокупности;
Общая дисперсия измеряет
межгрупповая дисперсия – это мера колеблемости частных средних по группами вокруг общей средней;
Межгрупповая дисперсия характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основание группировки.
xi и ni - соответственно средние и численности по отдельным группам.
Внутригрупповая дисперсия отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки.
и средняя из внутригрупповых дисперсий
Слайд 7Свойства дисперсии
Общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсии.
2. Если из всех значений вариант отнять какое-то постоянное число А, то средний квадрат отклонений от этого не изменится.
3. Если все значения вариант разделить на какое-то постоянное число А, то средний квадрат отклонений уменьшится от этого в А раз, а среднее квадратическое отклонение в А раз:
4. Дисперсия равна разности средней из квадратов значений признака и квадрата средней арифметической (способ моментов).
Слайд 9Пример 2: Определить групповые дисперсии, среднюю из групповых дисперсий, межгрупповую дисперсию,
Слайд 10Решение:
Для расчета групповых дисперсий вычислим средние по каждой группе:
Промежуточные расчеты дисперсий
Средняя из групповых дисперсий
Затем рассчитаем межгрупповую дисперсию. Для этого предварительно определим общую среднюю как среднюю взвешенную из групповых средних:
Теперь определим межгрупповую дисперсию:
Таким образом, общая дисперсия по правилу сложения дисперсий