двух переменных; комбинационный автомат и автомат с памятью
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основные понятия алгебры логики презентация
Содержание
- 1. Основные понятия алгебры логики
- 2. Введение Если аргументы функции принимают только значения
- 3. Определение Алгебра логики – это исчисление булевых функций на основе тождеств.
- 4. Виды логических схем Логические схемы комбинационного
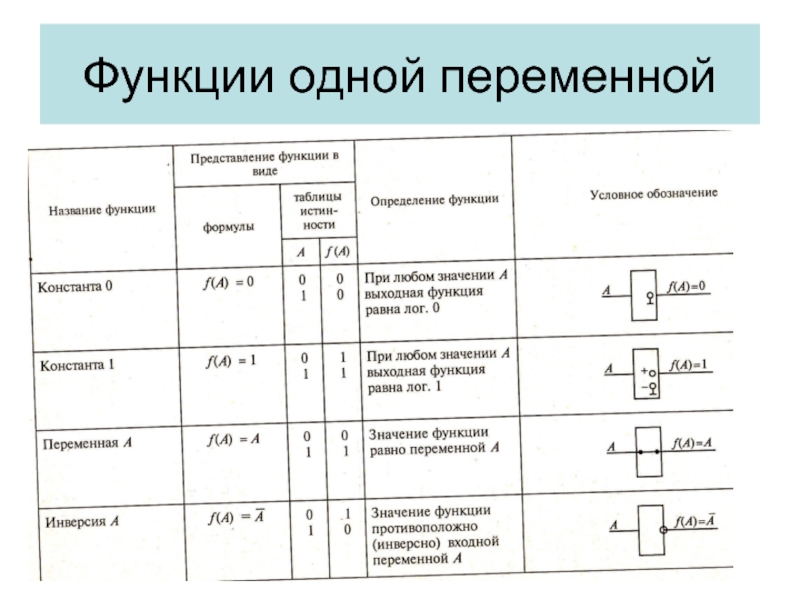
- 5. Функции одной переменной
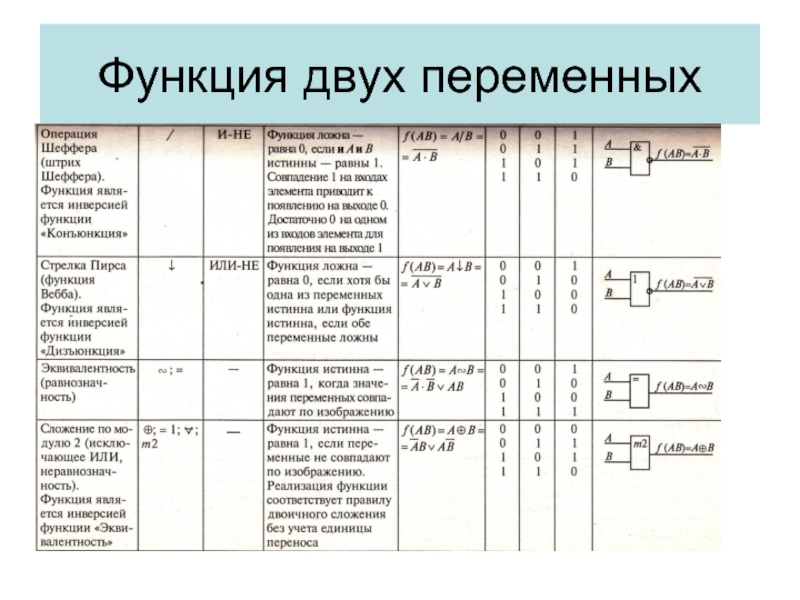
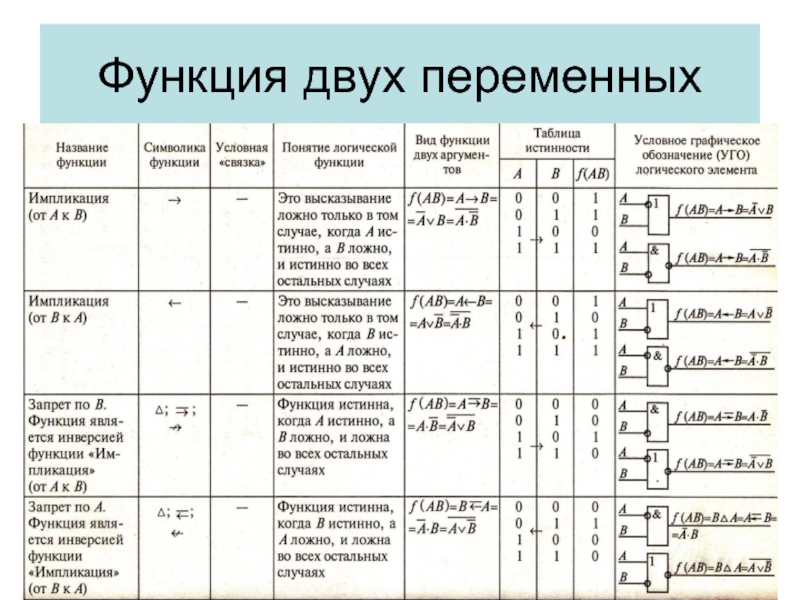
- 6. Функция двух переменных
- 7. Функция двух переменных
- 8. Функция двух переменных
- 9. Функциональное изображение логических элементов с двумя входами
- 10. Булевы тождества ВАЖНО. Одну и туже булеву
- 11. Тождества Коммутативные (переместительные) законы: Ассоциативные (сочетательные) законы:
- 12. Тождества Дистрибутивные (распределительные) законы: Законы повторения: Законы инверсии (двойственности):
- 13. Тождества Закон отрицания. Закон двойного отрицания. Закон поглощения. Закон склеивания.
- 14. Тождества их применение Операции с константами. и
- 15. Сводный список тождеств ЗАДАЧА. Дайте графическую интерпретацию этих тождеств
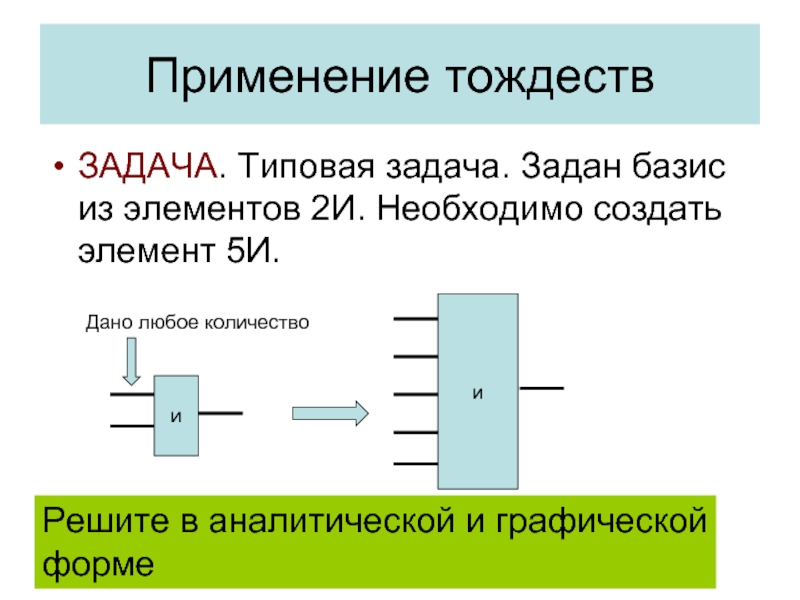
- 16. Применение тождеств ЗАДАЧА. Типовая задача. Задан
- 17. Используется для перехода от одного логического базиса
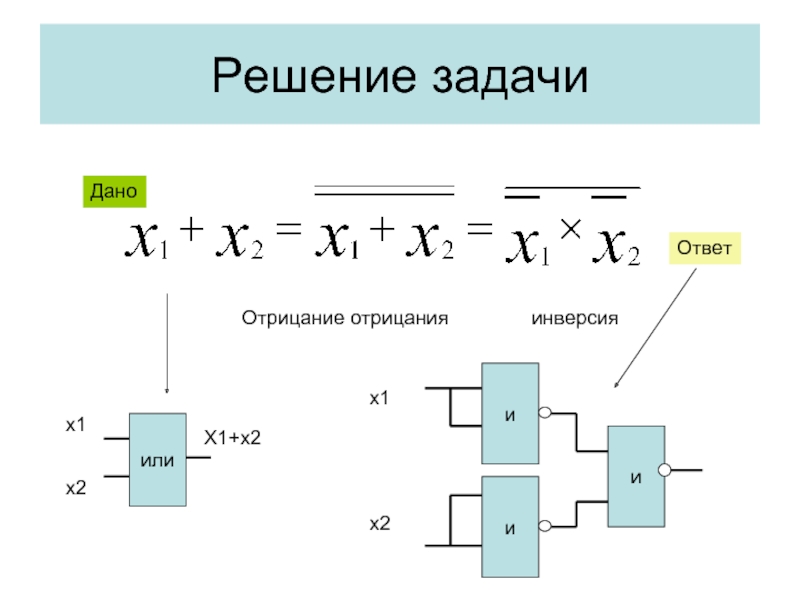
- 18. Решение задачи Отрицание отрицания инверсия или х1
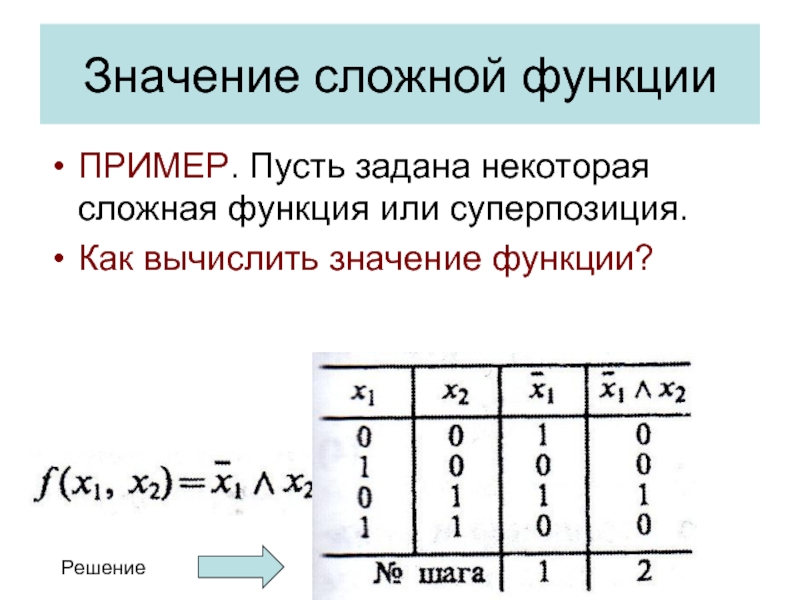
- 19. Значение сложной функции ПРИМЕР. Пусть задана некоторая
- 20. Пример 2. Вычислить значение функции. Значение сложной функции Из этой методики следует важное следствие
- 21. Логические выражения и логические схемы Задача. По формуле составьте изображение логической схемы
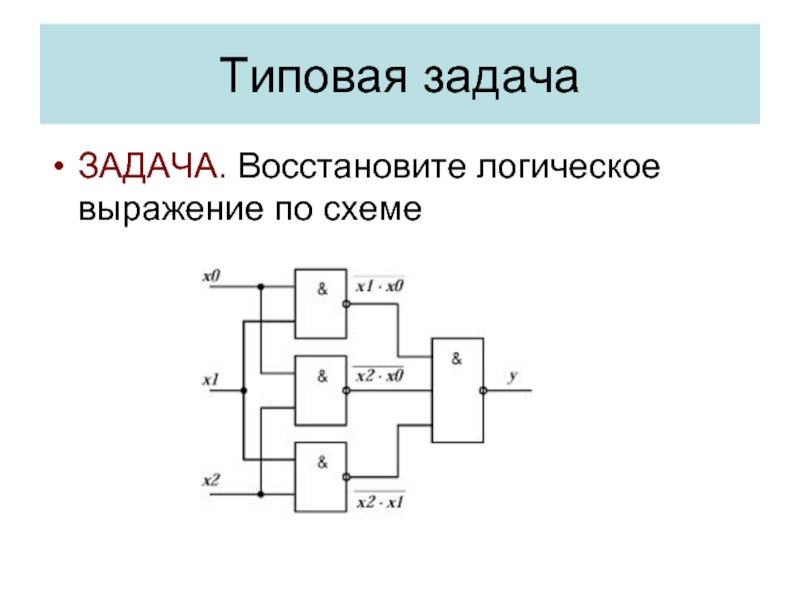
- 22. Типовая задача ЗАДАЧА. Восстановите логическое выражение по схеме
- 23. Булева функция N переменных ТЕОРЕМА. Любую булеву
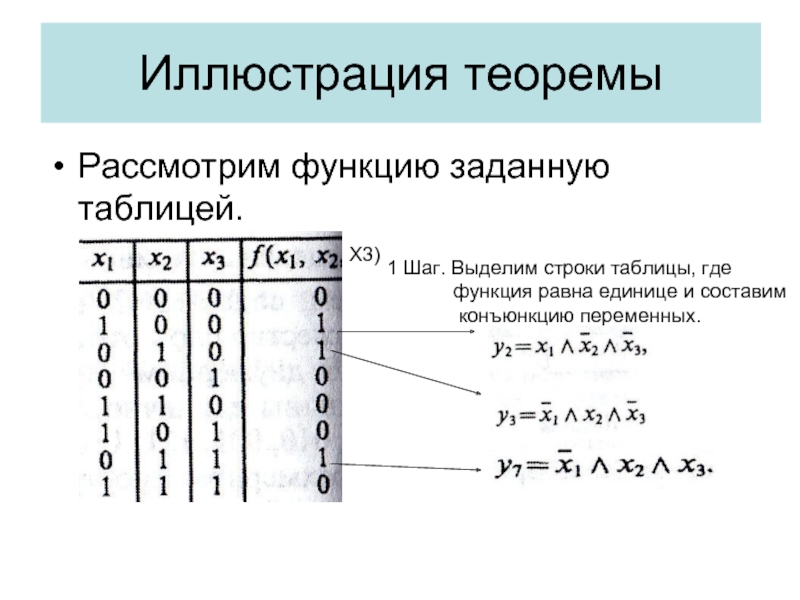
- 24. Иллюстрация теоремы Рассмотрим функцию заданную таблицей. 1
- 25. Шаг 2. Строим дизъюнкцию построенных конъюнкций. Продолжение
- 26. Дизъюнктивная и конъюнктивная нормальные формы представления функций
- 27. Определения Произведение переменных, в которое каждая из
- 28. Минтерм, макстерм, ранг Количество переменных, входящих в минтерм и макстерм, называется рангом
- 29. Пример Задана функция от двух переменных, как будут выглядеть минтермы и макстермы этой функции.
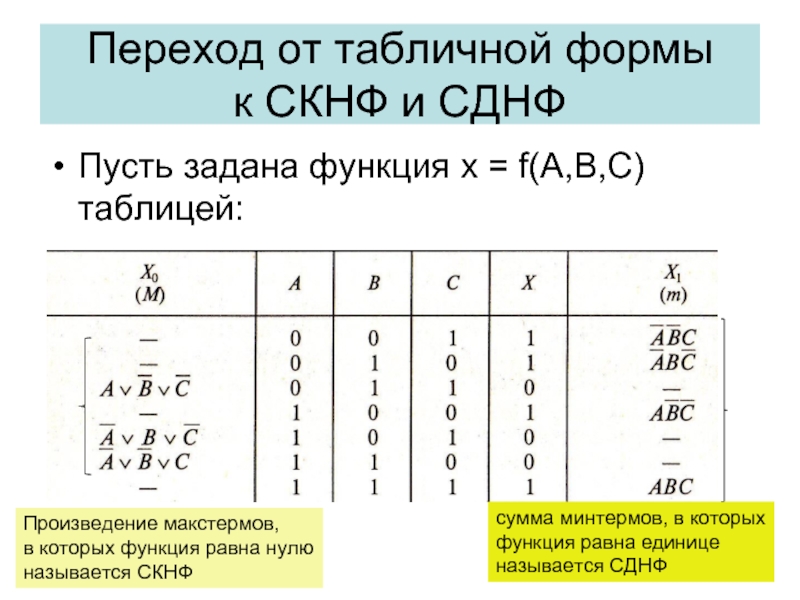
- 30. Переход от табличной формы к СКНФ
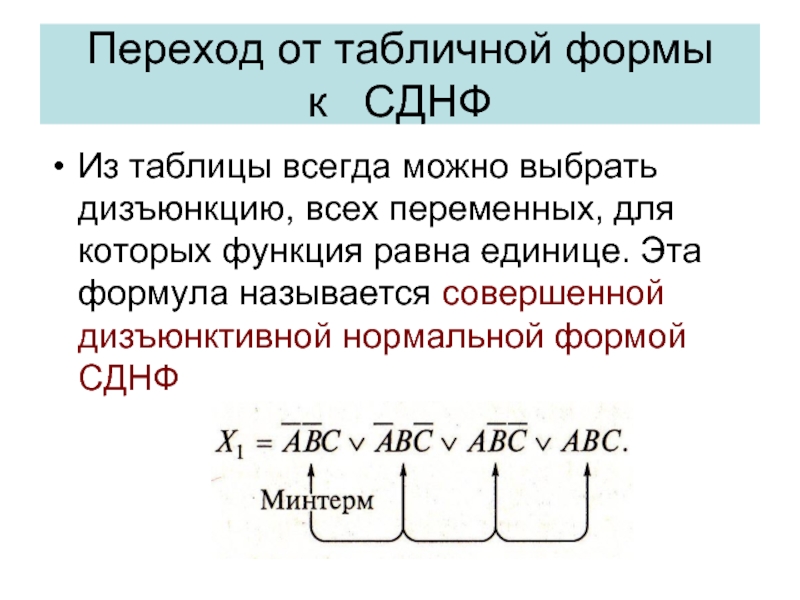
- 31. Из таблицы всегда можно выбрать дизъюнкцию, всех
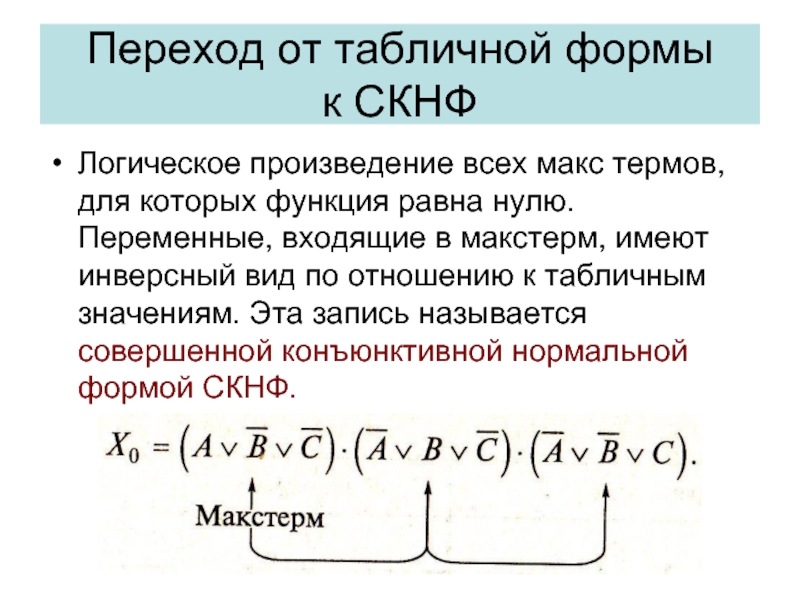
- 32. Логическое произведение всех макс термов, для которых
- 33. Неформальная и формальная постановка задачи Неформальная постановка
Введение Если аргументы функции принимают только значения 0 или 1, то функция так же может принимать значения 0 или 1. Независимая переменная, которая принимает всего два значения называется двоичной или логической
Слайд 2Введение
Если аргументы функции принимают только значения 0 или 1, то функция
так же может принимать значения 0 или 1.
Независимая переменная, которая принимает всего два значения называется двоичной или логической или булевой переменной.
Логическая схема, реализует функцию от заданного числа аргументов.
Разделяют функции от одного аргумента, от двух аргументов и от n – аргументов.
Независимая переменная, которая принимает всего два значения называется двоичной или логической или булевой переменной.
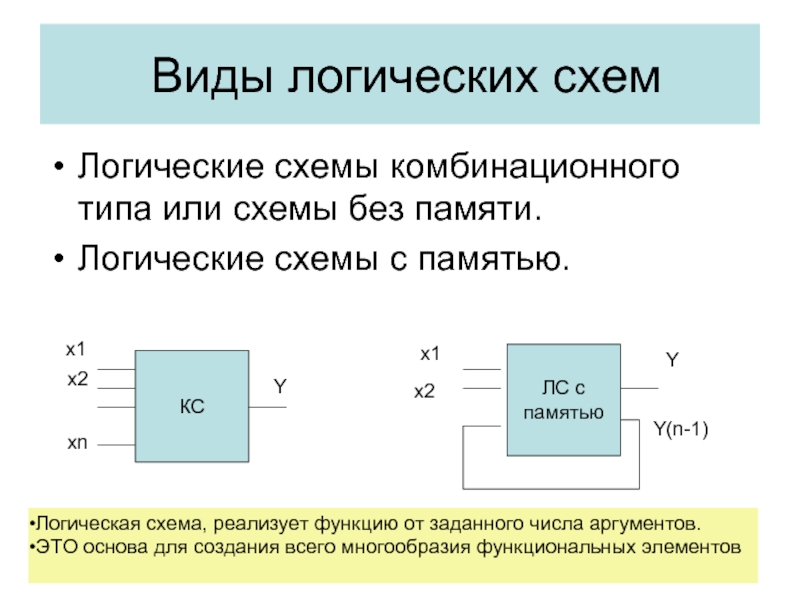
Логическая схема, реализует функцию от заданного числа аргументов.
Разделяют функции от одного аргумента, от двух аргументов и от n – аргументов.
Слайд 4 Виды логических схем
Логические схемы комбинационного типа или схемы без памяти.
Логические
схемы с памятью.
КС
ЛС с
памятью
х1
х1
х2
х2
хn
Y
Y
Y(n-1)
Логическая схема, реализует функцию от заданного числа аргументов.
ЭТО основа для создания всего многообразия функциональных элементов
Слайд 9Функциональное изображение логических элементов с двумя входами
Основа для создания
любой цифровой схемы
Обычные
логические
выходы нельзя
Соединять!!!!
выходы нельзя
Соединять!!!!
Слайд 10Булевы тождества
ВАЖНО. Одну и туже булеву функцию можно задать разными формулами.
Это и есть тождества.
Использую тождества можно менять аналитическое выражение функции, не изменяя ее значение.
Использую тождества можно менять аналитическое выражение функции, не изменяя ее значение.
Слайд 12Тождества
Дистрибутивные (распределительные) законы:
Законы повторения:
Законы инверсии (двойственности):
Слайд 16Применение тождеств
ЗАДАЧА. Типовая задача. Задан базис из элементов 2И. Необходимо
создать элемент 5И.
и
и
Решите в аналитической и графической
форме
Дано любое количество
Слайд 17Используется для перехода от одного логического базиса к другому.
ЗАДАЧА. Задан базис
элементов 2И-НЕ. Постройте из этого базиса логический элемент 2ИЛИ
Применение тождеств
Слайд 19Значение сложной функции
ПРИМЕР. Пусть задана некоторая сложная функция или суперпозиция.
Как вычислить
значение функции?
Решение
Слайд 20Пример 2. Вычислить значение функции.
Значение сложной функции
Из этой методики следует важное
следствие
Слайд 21Логические выражения и логические схемы
Задача. По формуле составьте изображение логической схемы
Слайд 23Булева функция N переменных
ТЕОРЕМА. Любую булеву функцию n переменных можно задать
с помощью формулы, употребляя только тождественный нуль, отрицание, конъюнкцию и дизъюнкцию.
Далее приведем пример
Далее приведем пример
Слайд 24Иллюстрация теоремы
Рассмотрим функцию заданную таблицей.
1 Шаг. Выделим строки таблицы, где
функция равна единице и составим
конъюнкцию переменных.
конъюнкцию переменных.
Х3)
Слайд 25Шаг 2. Строим дизъюнкцию построенных конъюнкций.
Продолжение иллюстрации теоремы
Функция стоящая в правой
части равенства называется
нормальной дизъюнктивной формой
нормальной дизъюнктивной формой
По формуле можно построить логическую схему устройства, условно
кодера, которая будет принимать значение единица при определенных
комбинациях х.
Слайд 26Дизъюнктивная и конъюнктивная нормальные формы представления функций в алгебре логики
Чтобы знать
переключательную функцию, необязательно задавать все ее значения при всех сочетаниях переменных. Достаточно знать состояния, при которых она равна единице.
В аналитическом виде функция в своей основе имеет набор логических произведений или сумм, связанных знаками сумм или произведений.
В аналитическом виде функция в своей основе имеет набор логических произведений или сумм, связанных знаками сумм или произведений.
Слайд 27Определения
Произведение переменных, в которое каждая из переменных входит только один раз
в прямом или инверсном виде, называется минтермом.
Сумма переменных, в которую каждая из переменных входит только один раз в прямом или инверсном виде, называется макстремом.
Сумма переменных, в которую каждая из переменных входит только один раз в прямом или инверсном виде, называется макстремом.
Слайд 28Минтерм, макстерм, ранг
Количество переменных, входящих в минтерм и макстерм, называется
рангом
Слайд 29Пример
Задана функция от двух переменных, как будут выглядеть минтермы
и макстермы
этой функции.
Слайд 30Переход от табличной формы
к СКНФ и СДНФ
Пусть задана функция х
= f(А,B,C) таблицей:
сумма минтермов, в которых
функция равна единице
называется СДНФ
Произведение макстермов,
в которых функция равна нулю
называется СКНФ
Слайд 31Из таблицы всегда можно выбрать дизъюнкцию, всех переменных, для которых функция
равна единице. Эта формула называется совершенной дизъюнктивной нормальной формой СДНФ
Переход от табличной формы
к СДНФ
Слайд 32Логическое произведение всех макс термов, для которых функция равна нулю. Переменные,
входящие в макстерм, имеют инверсный вид по отношению к табличным значениям. Эта запись называется совершенной конъюнктивной нормальной формой СКНФ.
Переход от табличной формы
к СКНФ
Слайд 33Неформальная и формальная
постановка задачи
Неформальная постановка задачи:
Необходимо разработать устройство для автомобиля с
кузовом седан. Устройство должно обладать звуковым и световым сигнализатором и срабатывать если водитель находится на своем сидении и открыта хотя бы одна дверь или багажник.
ЗАДАЧА. Сформулируйте логическое выражение и логическую схему устройства.
ЗАДАЧА. Сформулируйте логическое выражение и логическую схему устройства.
