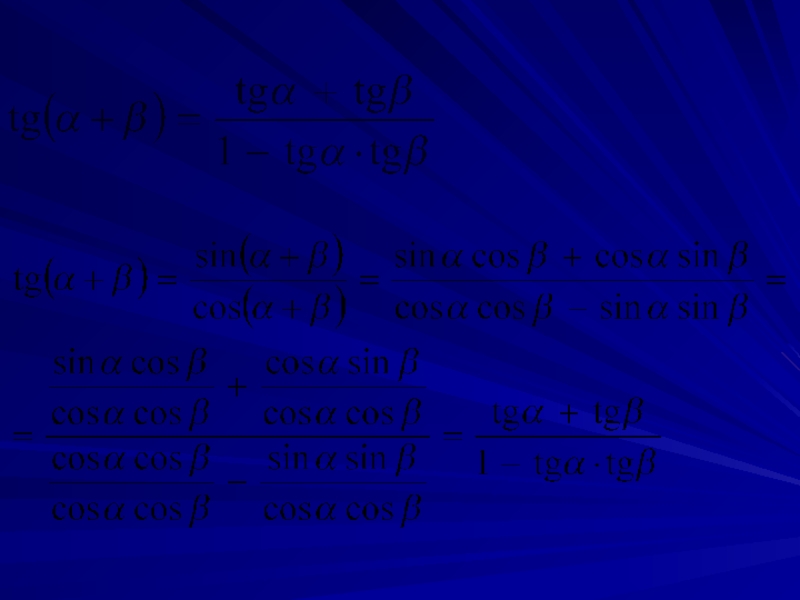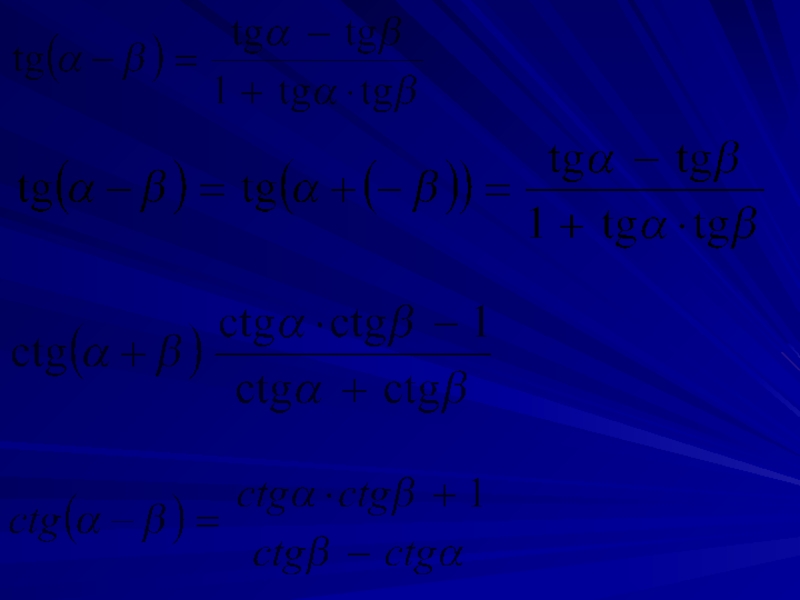- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тригонометрические формулы презентация
Содержание
- 1. Тригонометрические формулы
- 2. Синусом угла α называется ордината точки,
- 3. X (cos) y (sin)
- 4. Y cos ctg tg sin
- 5. Знаки тригонометрических функций х y (sin)
- 6. Свойство четности (нечетности) sin(-α) = -sinα, нечетная,
- 7. 1. Соотношения между тригонометрическими функциями
- 8. 1. Соотношения между тригонометрическими функциями
- 9. Формулы приведения Тригонометрические функции углов вида
- 10. Формулы приведения sin(π+α) = - sinα,
- 11. Формулы приведения sin(π - α) =
- 12. Формулы приведения sin(2π+α) = sinα,
- 13. Формулы приведения sin(2π - α) = -
- 14. Формулы приведения sin( + α)
- 15. Формулы приведения sin( - α)
- 16. Формулы приведения X (cos)
- 17. Формулы приведения X (cos)
- 18. 2. Формулы сложения и вычитания аргументов
- 19. cos(α+β) = cosα • cosβ - sinα
- 22. 3. Формулы двойных и тройных углов sin2α
- 23. sin3α = 3sinα - 4 sin3α
- 25. 4. Преобразование в произведение сумм sinα ± sinβ, cosα ± cosβ
- 26. 5. Формулы половинного аргумента
- 27. 6. Формулы универсальной подстановки
- 28. 7. Преобразование произведений в суммы или разности
- 29. 8. Преобразование выражений acosα + bsinα путем введения вспомогательного угла
- 30. Утверждение доказано
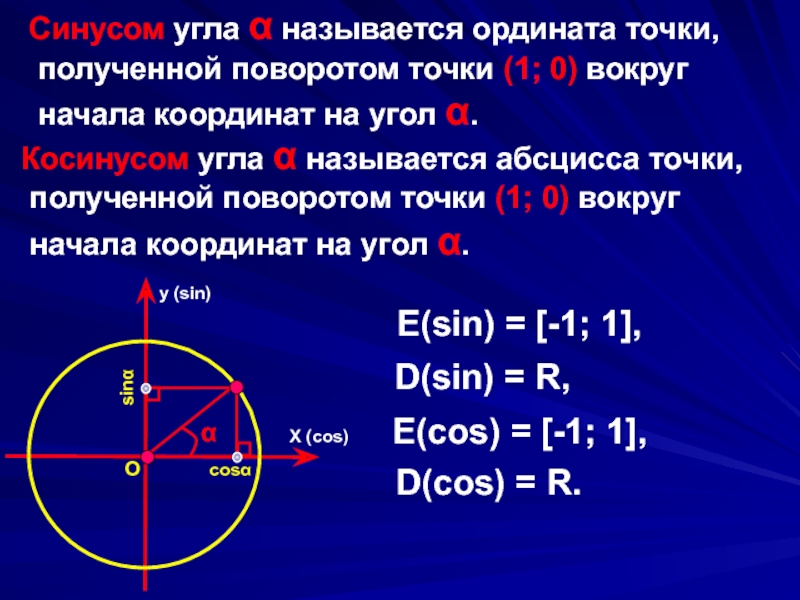
Слайд 2Синусом угла α называется ордината точки,
полученной поворотом точки (1;
начала координат на угол α.
Косинусом угла α называется абсцисса точки,
полученной поворотом точки (1; 0) вокруг
начала координат на угол α.
E(sin) = [-1; 1],
D(sin) = R,
E(cos) = [-1; 1],
D(cos) = R.
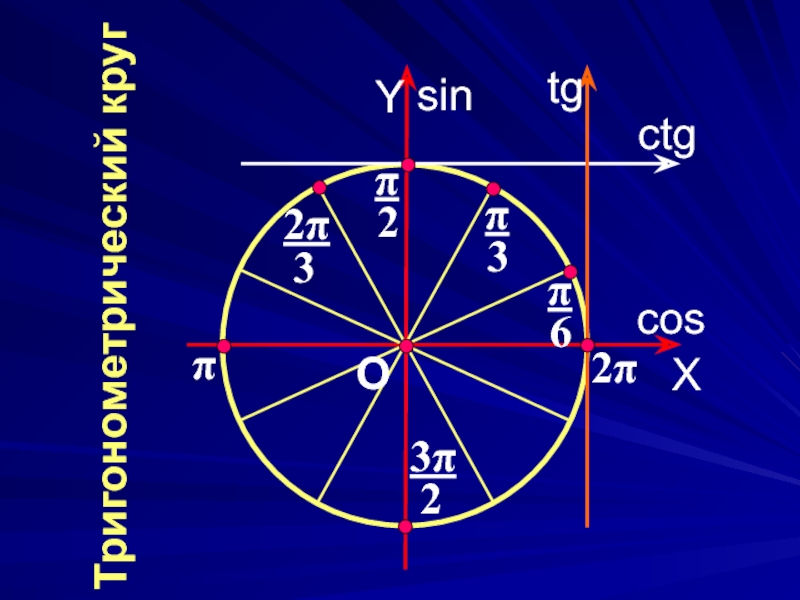
Слайд 3
X (cos)
y (sin)
α
O
cosα
sinα
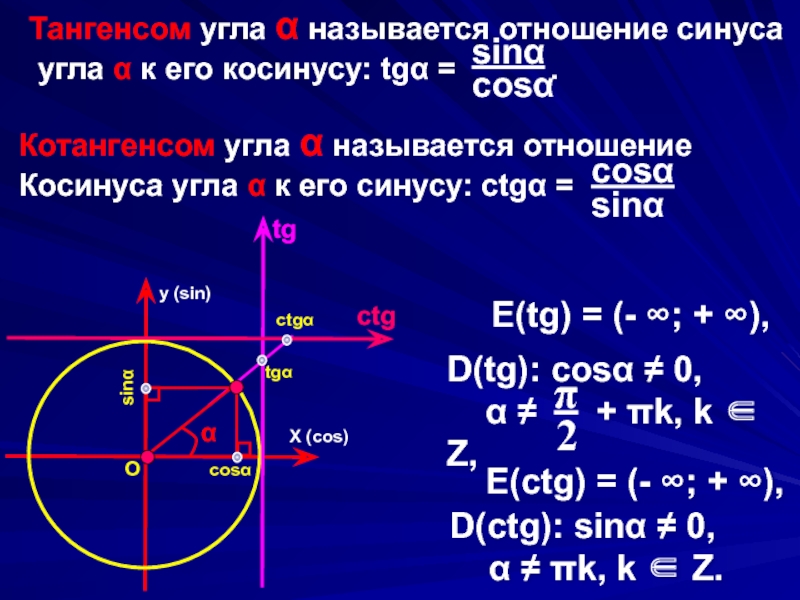
E(tg) = (- ∞; + ∞),
D(tg): cosα ≠ 0,
α ≠ + πk, k ∈ Z,
Котангенсом угла α называется отношение
Косинуса угла α к его синусу: ctgα =
E(ctg) = (- ∞; + ∞),
D(ctg): sinα ≠ 0,
α ≠ πk, k ∈ Z.
tg
ctg
tgα
ctgα
Тангенсом угла α называется отношение синуса
угла α к его косинусу: tgα = .
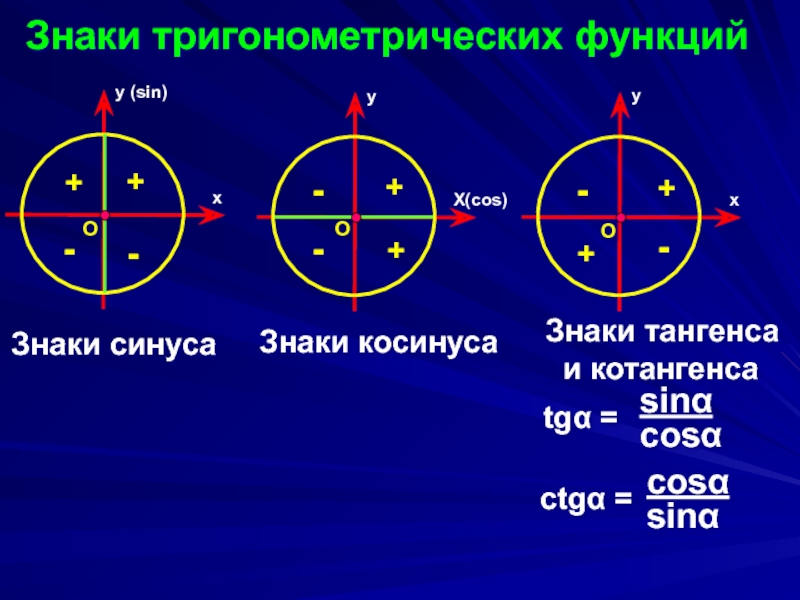
Слайд 5Знаки тригонометрических функций
х
y (sin)
O
Х(cos)
y
O
х
y
O
+
+
-
-
+
+
-
-
+
-
-
+
Знаки синуса
Знаки косинуса
Знаки тангенса
и котангенса
tgα
ctgα =
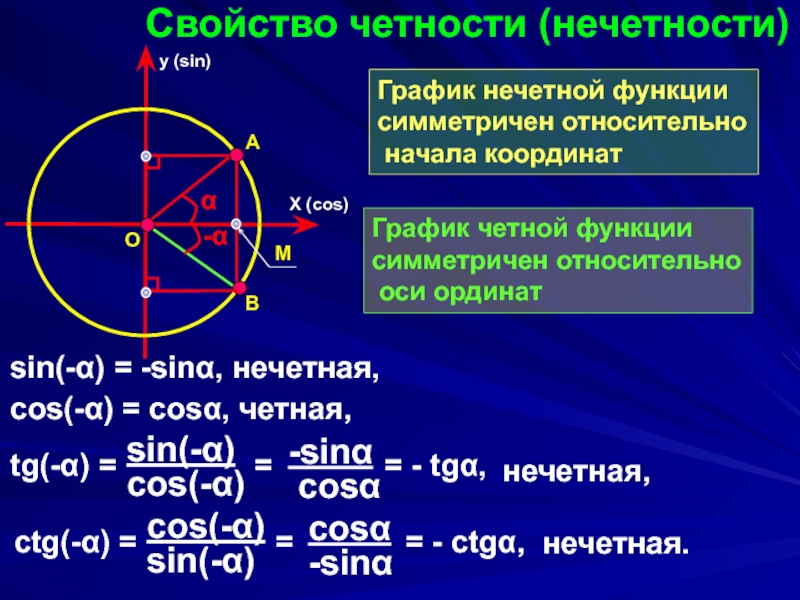
Слайд 6Свойство четности (нечетности)
sin(-α) = -sinα, нечетная,
X (cos)
y (sin)
α
O
-α
А
В
М
cos(-α) = cosα, четная,
нечетная,
нечетная.
График
симметричен относительно
начала координат
График четной функции
симметричен относительно
оси ординат
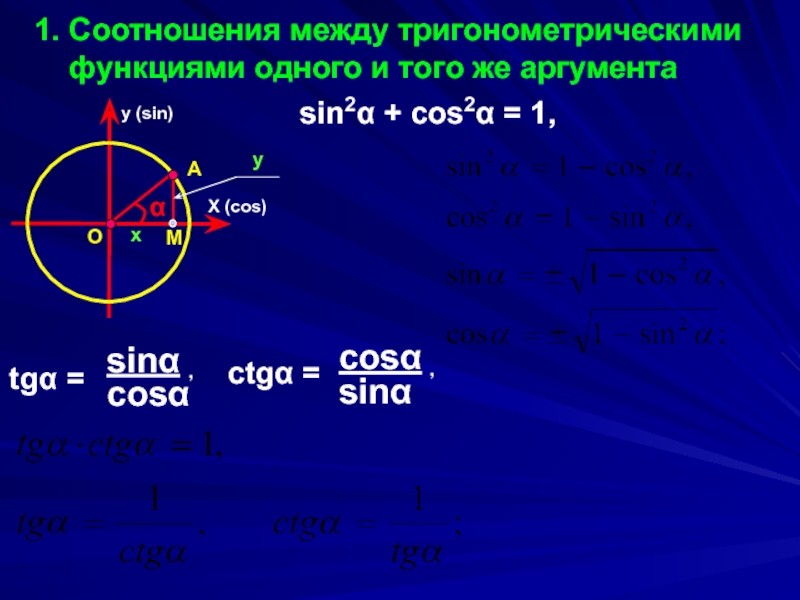
Слайд 71. Соотношения между тригонометрическими
функциями одного и того же аргумента
X
sin2α + cos2α = 1,
tgα =
y (sin)
α
O
А
М
х
у
,
,
Слайд 81. Соотношения между тригонометрическими
функциями одного и того же аргумента
sin2α
sin2α + cos2α = 1 ⎜ : sin2α ≠ 0
Слайд 9Формулы приведения
Тригонометрические функции углов вида
± α, π
могут быть выражены через функции угла α с
помощью формул, которые называются
формулами приведения.
Для углов π ± α и 2π ± α название исходной
функции сохраняется, для углов ± α, ± α
название исходной функции меняется:
синус на косинус, косинус на синус, тангенс на
котангенс, котангенс на тангенс.
2. Знак функции определяется, используя
тригонометрическую окружность.
Слайд 10
Формулы приведения
sin(π+α) = - sinα,
X (cos)
y (sin)
α
O
А
М
π + α
В
N
cos(π+α) =
tg(π+α) = tgα,
ctg(π+α) = ctgα;
Слайд 11
Формулы приведения
sin(π - α) = sinα,
X (cos)
y (sin)
α
O
А
М
π-α
В
N
cos(π - α)
tg(π - α) = - tgα,
ctg(π - α) = - ctgα;
Слайд 12Формулы приведения
sin(2π+α) = sinα,
X (cos)
y (sin)
α
O
А
М
2π + α
cos(2π+α) = cosα,
tg(2π+α)
ctg(2π+α) = ctgα;
sin(2πk+α) = sinα, k∈Z,
cos(2πk+α) = cosα, k∈Z,
tg(2πk+α) = tgα, k∈Z,
ctg(2πk+α) = ctgα, k∈Z;
Слайд 13Формулы приведения
sin(2π - α) = - sinα,
X (cos)
y (sin)
α
O
А
М
2π -
В
cos(2π - α) = cosα,
tg(2π - α) = - tgα,
ctg(2π - α) = - ctgα;
Слайд 14
Формулы приведения
sin( + α) = cosα,
X (cos)
y (sin)
α
O
А
М
В
N
cos(
tg( + α) = - ctgα,
ctg( + α) = - tgα;
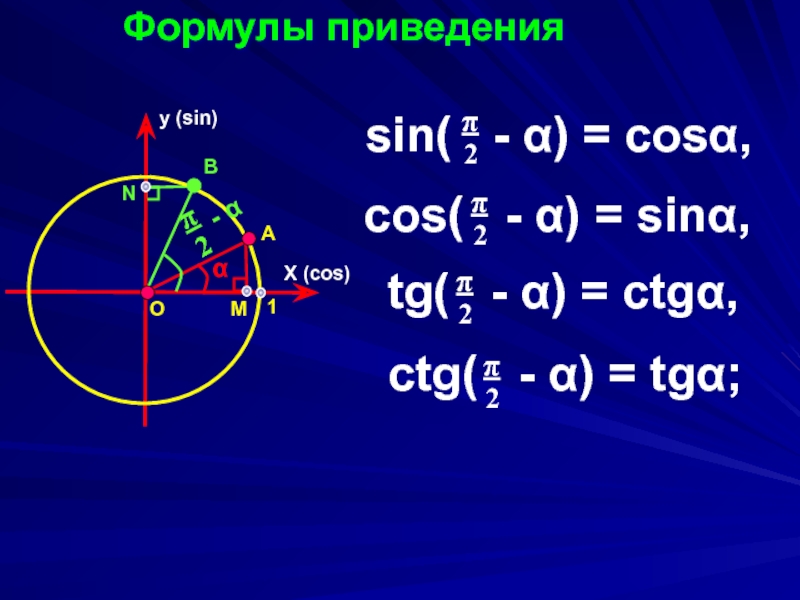
Слайд 15
Формулы приведения
sin( - α) = cosα,
X (cos)
y (sin)
α
O
А
М
В
N
cos(
tg( - α) = ctgα,
ctg( - α) = tgα;
Слайд 16
Формулы приведения
X (cos)
y (sin)
α
O
А
М
В
N
cos( + α) = sinα,
tg( +
ctg( + α) = - tgα;
Слайд 182. Формулы сложения и вычитания аргументов
cos(α-β) = cosα • cosβ + sinα • sinβ
X (cos)
y (sin)
α
O
Pα(cosα; sinα)
β
Pβ(cosβ; sinβ)
Слайд 19cos(α+β) = cosα • cosβ - sinα • sinβ
sin(α+β) = sinα
sin(α-β) = sinα • cosβ - cosα • sinβ
Слайд 223. Формулы двойных и тройных углов
sin2α = 2sinα cosα
sin2α = sin(α
cos2α = cos2α - sin2α = 2cos2α - 1 = 1 - 2sin2α
cos2α = cos(α + α) = cosαcosα - sinαsinα =
= cos2α - sin2α = cos2α - (1 – cos2α) = 2cos2α - 1
= 2(1 – sin2α) – 1 = 1 – 2sin2α
Слайд 23sin3α = 3sinα - 4 sin3α
sin3α = sin(α + 2α)
= sinα(1 - 2sin2α) + cosα 2sinαcosα =
= sinα - 2sin3α + 2cos2αsinα = sinα - 2sin3α +
+ 2(1 – sin2α)sinα = sinα - 2sin3α + 2sinα - 2sin3α =
= 3sinα - 4sin3α
cos3α = 4cos3α - 3cosα
cos3α = cos(α + 2α) = cosαcos2α - sinαsin2α =
= cosα(2cos2α - 1) - sinα 2sinαcosα =
= 2cos3α - cosα - 2sin2αcosα = 2cos3α - cosα -
- 2(1 – cos2α)cosα = 2cos3α - cosα - 2cosα + 2cos3α =
= 4cos3α - 3cosα