- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Общая постановка задачи оптимизации презентация
Содержание
- 1. Общая постановка задачи оптимизации
- 2. Целевая функция Известные переменные или функции
- 3. При заданных условиях найти такие значения
- 4. Если целевая функция, которую надо максимизировать задана
- 5. Когда переменных много, то решение системы уравнений,
- 6. Выявление всех процессов, происходящих в оптимизационной системе
- 7. Стратегия оптимизационных исследований
- 9. Составление математической модели
- 10. Целевая функция Целевая функция представляет собой математическое
- 11. Критерии оптимизации режимных задач Издержки производства на
- 12. Критерии оптимизации внутристанционных режимов электростанции Технические критерии,
- 13. Критерий оптимизации режимов электрической сети сетевого предприятия
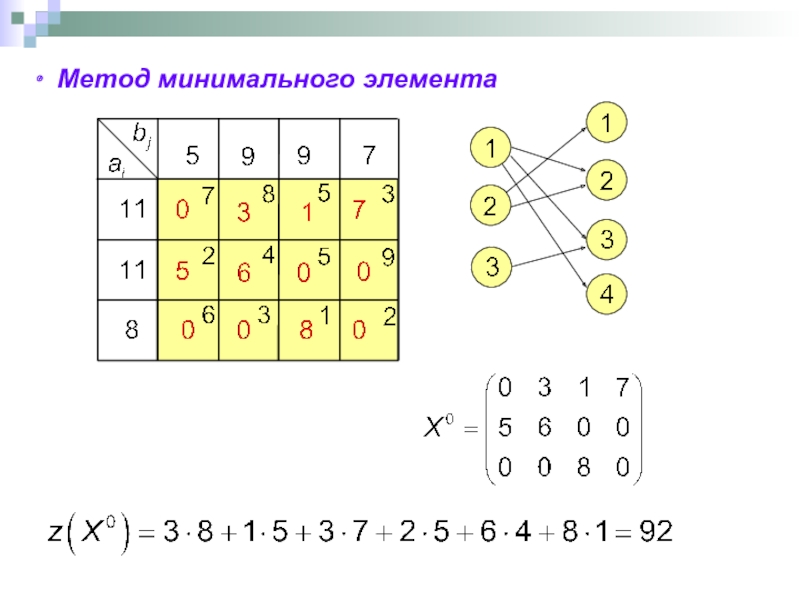
- 14. Критерий оптимизации режимов электрической сети для нескольких
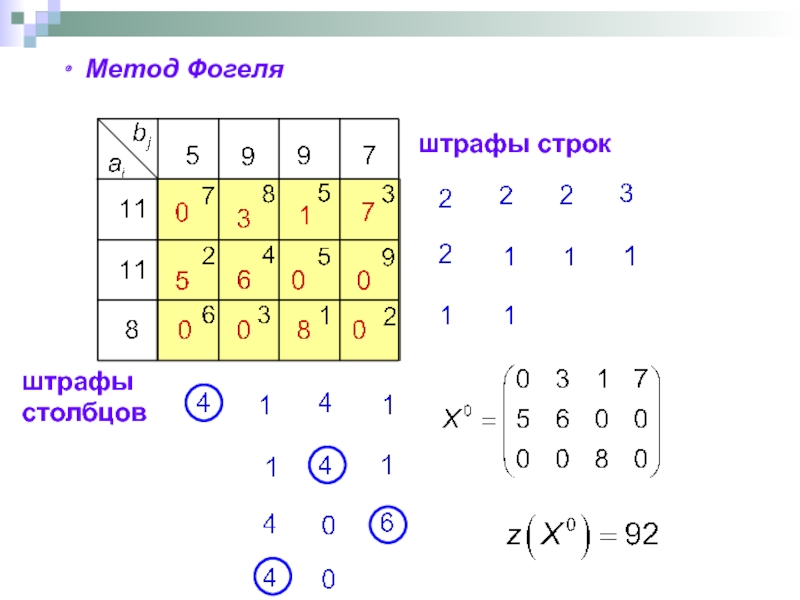
- 15. При оптимизации режима электроэнергетической системы Оптимизация режима
- 16. Ограничения на переменные
- 17. Ограничения могут быть в форме: Равенств, отражающих
- 18. В общем виде задача оптимизации формулируется
- 19. МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
- 20. Формирование математической модели по содержательной постановке задачи
- 21. Формирование математической модели по содержательной постановке задачи
- 22. Формирование математической модели по содержательной постановке задачи
- 23. Формирование математической модели по содержательной постановке задачи
- 24. Математические предположения для задачи ЛП: определенность
- 25. Линейное программирование Основная задача линейного программирования
- 26. Стандартная форма Первая стандартная форма задачи линейного программирования имеет вид
- 27. Стандартная форма Вторая стандартная форма задачи линейного программирования имеет вид
- 28. Каноническая форма Канонической формой задачи линейного программирования называется задача вида
- 29. Правила приведения Рассмотрим теперь те приёмы, которые
- 30. Правила приведения 2. Смена знака неравенства. Если
- 31. Правила приведения 3. Превращение равенства в систему
- 32. Правила приведения 4. Превращение неравенств в равенства.
- 33. Правила приведения То есть в неравенстве со
- 34. Математически задача ЛП – задача нахождения наибольшего
- 35. Вектор
- 36. Геометрический метод решения задачи ЛП
- 37. Теорема (об оптимальных экстремальных точках). Если в
- 38. При решении задачи ЛП возможны случаи:
- 39. Симплекс-метод решения задачи ЛП.
- 40. Стандартная задача минимизации Матричная и векторная форма записи
- 41. Каноническая задача максимизации (минимизации) Матричная и векторная форма записи
- 42. Эквивалентные преобразования. Нахождение максимума
- 43. Если имеется n таких переменных ,
- 44. Ограничение типа равенства можно заменить двумя
- 45. Базисное решение системы линейных уравнений Пусть
- 46. Базисным решением СЛУ, зависящим от множества индексов
- 47. Утверждение. Если у системы линейных
- 48. Перейдем к описанию формального алгоритма симплекс-метода для
- 49. Приведем данную систему к диагональной форме по переменным:
- 50. Симплексная таблица представляет собой таблицу коэффициентов диагональной
- 51. Классификация симплексных таблиц: симплексная таблица называется
- 52. Алгоритм прямого симплекс-метода (максимизация) 0. Начать вычисления
- 53. 2. Проверка условия неограниченности задачи ЛП
- 54. ведущий столбец ведущая строка алгоритм
- 55. Транспортная задача заключается
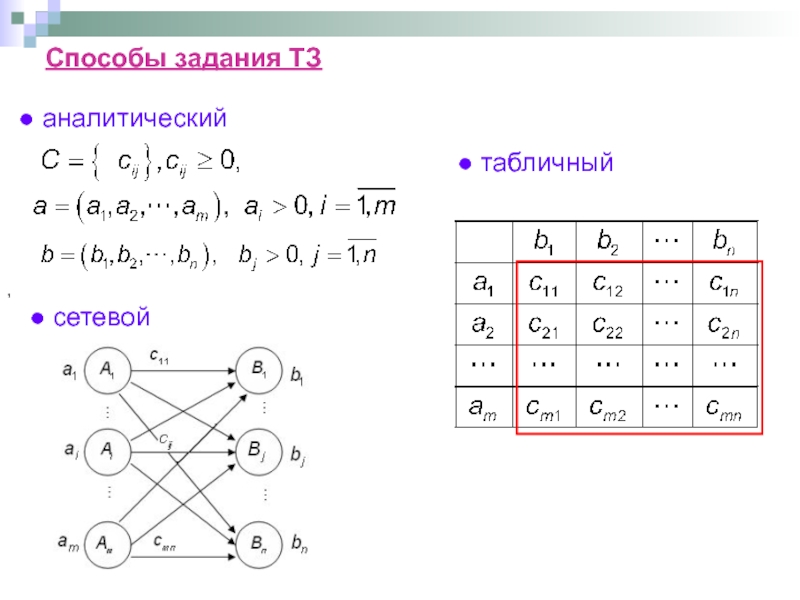
- 56. , Способы задания ТЗ
- 57. Математическая модель транспортной задачи Теорема
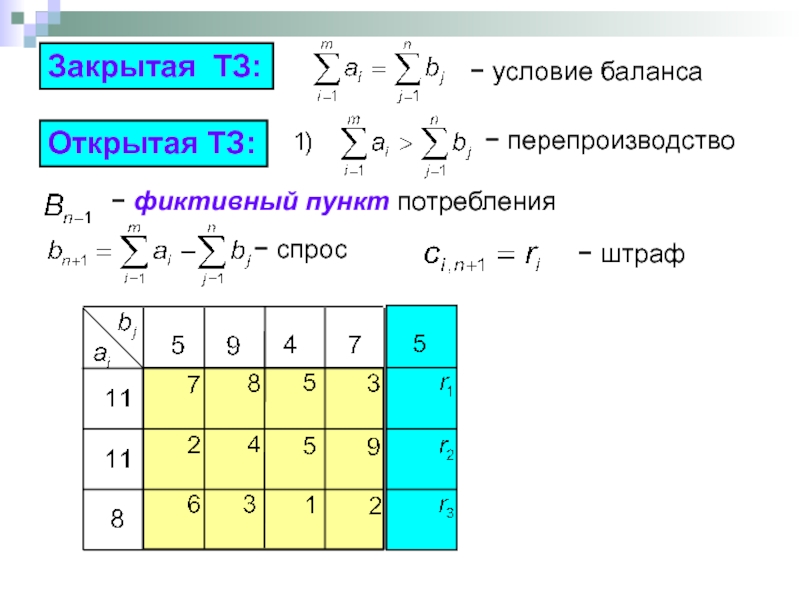
- 58. Закрытая ТЗ: Открытая ТЗ: − спрос − условие баланса − перепроизводство
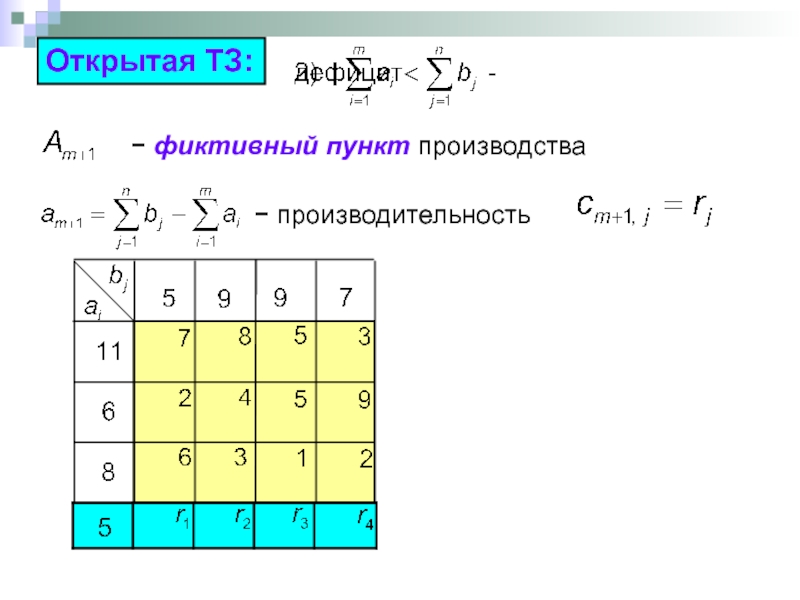
- 59. Открытая ТЗ:
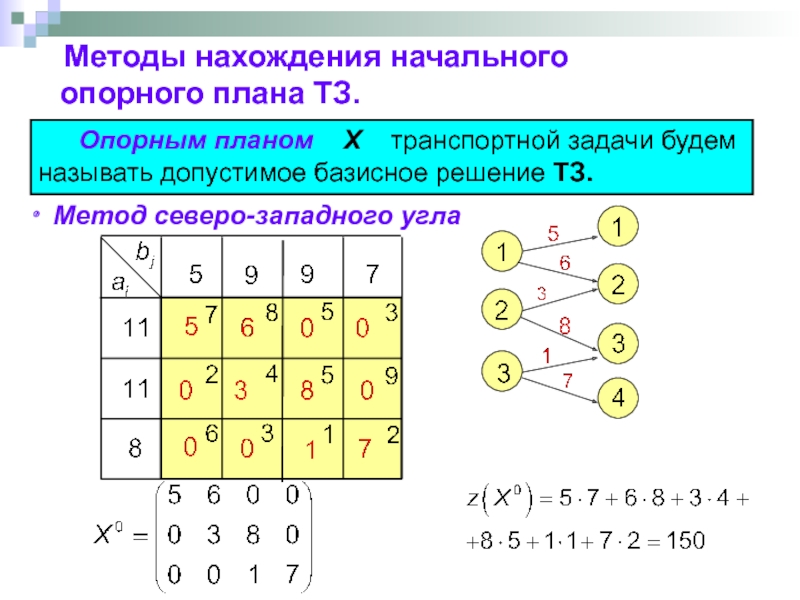
- 60. Методы нахождения начального
- 61. Метод минимального элемента
- 62. Метод Фогеля штрафы строк штрафы столбцов
- 63. Проверка плана ТЗ на опорность (метод
Слайд 2Целевая функция
Известные переменные или функции
Зависящие от нас факторы или неизвестные переменные
Целевая функция зависит от обеих групп факторов
Слайд 3При заданных условиях
найти такие значения ,
которые обращают показатель
Математическая задача оптимизации
Слайд 4Если целевая функция, которую надо максимизировать задана в следующем виде и
Производные равны
Ограниченное применение метода дифференцирования для решения задачи оптимизации
Слайд 5Когда переменных много, то решение системы уравнений, полученное дифференцированием, зачастую оказывается
Ограниченное применение метода дифференцирования для решения задачи оптимизации
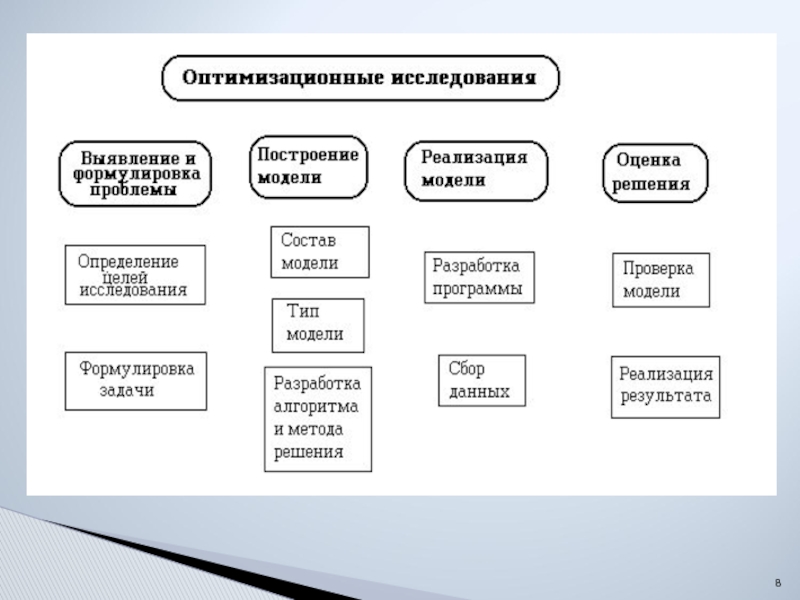
Слайд 6Выявление всех процессов, происходящих в оптимизационной системе для получения полной характеристики
Содержательная постановка задачи оптимизации для построения математической модели и выбор метода решения. Здесь главное отнесение задачи к определенному классу (развитие или функционирование), выбор критерия оптимизации и целевой функции.
Составление математической модели.
Определение математического метода решения задачи.
Разработка алгоритма решения задачи и собственно решение (как правило, на компьютере при наличие соответствующей программы).
Принятие оптимального решения специалистом на базе полученного решения.
Этапы постановки и решения оптимизационных задач
Слайд 10Целевая функция
Целевая функция представляет собой математическое выражение, дающее количественную оценку степени
- вектор заданных и зависимых (неизвестных) переменных
Слайд 11Критерии оптимизации режимных задач
Издержки производства на эксплуатацию и развитие
Критерии управления предприятием
Слайд 12Критерии оптимизации внутристанционных режимов электростанции
Технические критерии, которые могут быть представлены величинами
для ТЭС – минимум расхода топлива
либо для любой станции максимум КПД
Оптимизация режимов направлена на выбор оптимального состава работающего оборудования, активных и реактивных мощностей агрегатов.
Слайд 13Критерий оптимизации режимов электрической сети сетевого предприятия
Минимума потерь активной мощности
Минимума потерь
Слайд 14Критерий оптимизации режимов электрической сети для нескольких сетевых предприятий, взаимодействующих при
В интересах покупателей применяется критерий минимума стоимости передачи энергии всех сетевых предприятий, по которому определяются транспортные потоки мощностей
Слайд 15При оптимизации режима электроэнергетической системы
Оптимизация режима может проводиться в различных задачах
Слайд 17Ограничения могут быть в форме:
Равенств, отражающих зависимость между переменными. Они основываются
Неравенств, отражающих предельно допустимые значения переменных (граничные условия) или двухсторонние неравенства
или однозначные
Слайд 20Формирование математической модели по содержательной постановке задачи
Задача о рациональном использовании ресурсов
Задача о рациональной загрузке оборудования
Транспортная задача
Задача о рациональной смеси
Слайд 21Формирование математической модели по содержательной постановке задачи
1-я группа – задачи, строго
- транспорт материалов и зап.частей;
- распределение топлива на складах;
- расстановка ремонтных бригад на трассе.
Слайд 22Формирование математической модели по содержательной постановке задачи
2-я группа – задачи высокой
Слайд 23Формирование математической модели по содержательной постановке задачи
3-я группа – задачи, допускающие
Слайд 24Математические предположения для задачи ЛП:
определенность (детерминированность) – все параметры модели
линейность (эквивалентна пропорциональности и аддитивности) – все функциональные соотношения модели линейны относительно основных переменных;
пропорциональность – эффект влияния переменной задачи пропорционален значению этой переменной;
аддитивность – эффект влияния нескольких переменных задачи равен сумме эффектов от каждой переменной;
делимость – все основные переменные задачи могут принимать произвольные вещественные значения в определенном диапазоне (бесконечно делимы).
Слайд 28Каноническая форма
Канонической формой задачи линейного программирования называется задача вида
Слайд 29Правила приведения
Рассмотрим теперь те приёмы, которые позволяют произвольные формы задач линейного
1. Превращение max в min и наоборот.
Если целевая функция в задаче линейного программирования задана в виде
то, умножая её на (- 1), приведем её к виду
так как смена знака приводит к смене min на max.
Аналогично можно заменить max на min.
,
Слайд 30Правила приведения
2. Смена знака неравенства.
Если ограничение задано в виде
то, умножая на
Аналогично, неравенство вида больше либо равно можно превратить в неравенство вида меньше либо равно .
Слайд 31Правила приведения
3. Превращение равенства в систему неравенств.
Если ограничение задано в виде
то его можно заменить эквивалентной системой двух неравенств
или такой же системой неравенств со знаками больше либо равно.
Указанные выше приемы позволяют приводить задачи линейного программирования к стандартной форме.
Слайд 32Правила приведения
4. Превращение неравенств в равенства.
Для приведения задачи к канонической форме,
Слайд 33Правила приведения
То есть в неравенстве со знаком меньше либо равно добавляют
В целевую функцию эти дополнительные переменные включают с коэффициентом 0, т.е. фактически они в целевой функции отсутствуют.
Получив решение задачи в канонической форме, для получения решения исходной задачи надо просто выбросить из решения значения введенных дополнительных переменных.
Слайд 34Математически задача ЛП – задача нахождения наибольшего (наименьшего) значения линейной функции
задача максимизации ЛП
при ограничениях
задача минимизации ЛП
при ограничениях
−заданные параметры
− условие неотрицательности переменной
− целевая функция
− переменные
Слайд 35 Вектор
Множеством допустимых решений задачи ЛП называется множество векторов ,
удовлетворяющих всем ограничениям задачи.
Вектор доставляющий максимум (минимум) функции z при заданных ограничениях, называется оптимальным решением задачи ЛП.
Наибольшее (наименьшее) значение целевой функции
называется значением задачи ЛП.
Решить задачу ЛП − означает найти оптимальное реше-
ние и значение целевой функции.
Слайд 36Геометрический метод решения задачи ЛП
Пример Решим графически задачу :
Геометрический метод реализуется
построение допустимого множества решений задачи ЛП;
нахождение оптимального решения задачи ЛП.
Слайд 37Теорема (об оптимальных экстремальных точках).
Если в задаче ЛП существует оптимальное решение,
Алгоритм графического метода для задач ЛП :
записать каждое ограничение как равенство и нарисовать прямую;
найти для каждого ограничения допустимую область и множество допустимых решений задачи ЛП;
найти градиент целевой функции
нарисовать линию уровня целевой функции
сдвигать линию уровня в направлении градиента, до последней точки пересечения с множеством доп. решений.
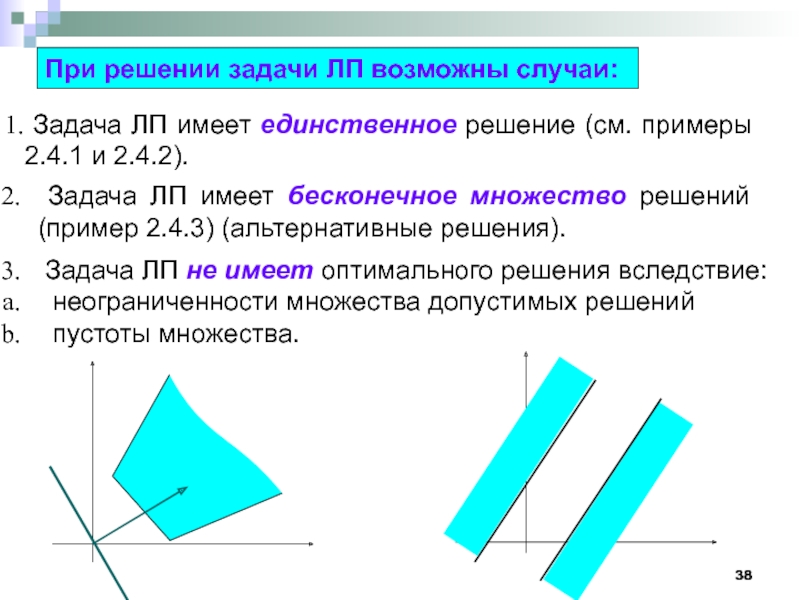
Слайд 38При решении задачи ЛП возможны случаи:
Задача ЛП имеет единственное
Задача ЛП имеет бесконечное множество решений (пример 2.4.3) (альтернативные решения).
Задача ЛП не имеет оптимального решения вследствие:
неограниченности множества допустимых решений
пустоты множества.
Слайд 39Симплекс-метод решения задачи ЛП.
Стандартная задача максимизации
Матричная и векторная форма записи
Слайд 42Эквивалентные преобразования.
Нахождение максимума линейной функции эквивалентно нахождению минимума этой
Если на переменную не накладывается условие неотрицательности, то ее можно заменить разностью двух неотрицательных переменных:
Слайд 43 Если имеется n таких переменных , то их можно заменить
Ограничение типа неравенства можно представить в виде равенства, используя слабые переменные, следующим образом:
Слайд 44 Ограничение типа равенства можно заменить двумя неравенствами:
Если имеется m
Знак неравенства можно заменить на противоположный, умножив данное неравенство на (-1)!
Слайд 45Базисное решение системы линейных уравнений
Пусть СЛУ AX =B совместна, т. е.
Слайд 46 Базисным решением СЛУ, зависящим от множества индексов
привести данную систему, используя метод Гаусса, к диагональной форме по переменным:
- базисные переменные
взяв небазисные переменные,
получим
Слайд 47
Утверждение.
Если у системы линейных уравнений существует
решение, то существует и
Утверждение.
Если задача ЛП имеет допустимое решение, то она имеет и допустимое базисное решение.
Утверждение.
Если задача ЛП имеет оптимальное решение, то она имеет и оптимальное базисное решение.
Слайд 48 Перейдем к описанию формального алгоритма симплекс-метода для канонической задачи максимизации:
Выполним ряд
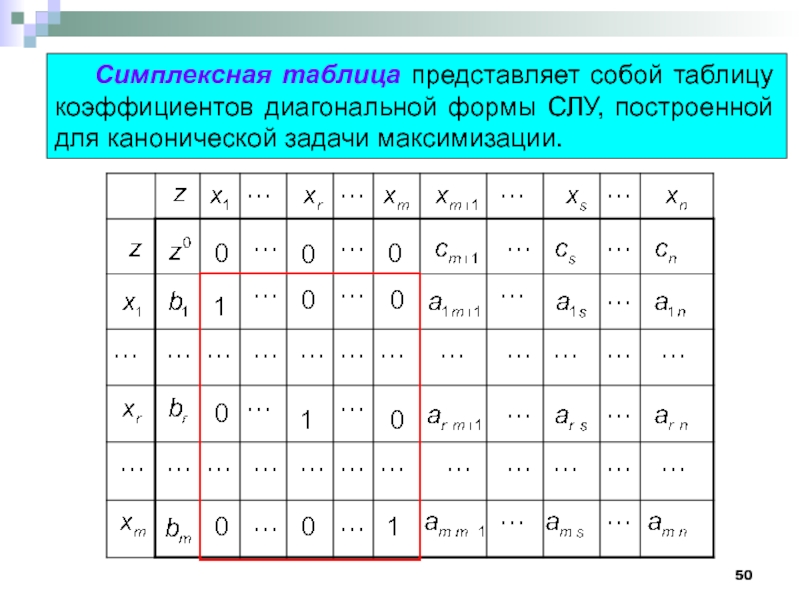
Слайд 50 Симплексная таблица представляет собой таблицу коэффициентов диагональной формы СЛУ, построенной для
Слайд 51Классификация симплексных таблиц:
симплексная таблица называется прямо-допустимой,
если
симплексная таблица
симплексная таблица называется оптимальной, если она одновременно и прямо-допустимая, и двойственно-допустимая. Оптимальная СТ соответствует оптимальному базисному решению.
Слайд 52Алгоритм прямого симплекс-метода (максимизация)
0. Начать вычисления с прямо-допустимой СТ.
В противном
номер которой находится по правилу:
Если то текущее базисное решение является оптимальным.
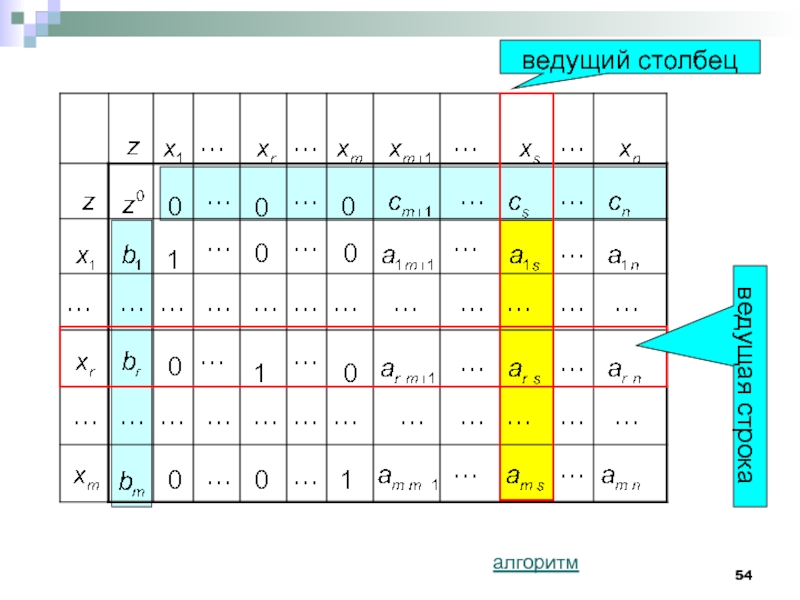
Столбец s называется ведущим столбцом СТ.
1. Проверка оптимальности или нахождение ведущего столбца СТ.
ИТЕРАЦИЯ
Слайд 53
2. Проверка условия неограниченности задачи ЛП или
нахождение ведущей строки СТ.
В противном случае следует выводить из базиса переменную, для которой:
Строка под номером r называется ведущей строкой СТ,
3. Преобразование СТ.
то решение задачи неограниченно.
− ведущим элементом СТ,
Слайд 55
Транспортная задача заключается в опре-делении плана перевозок, при котором удовлетворен спрос
Транспортная задача (ТЗ)
Содержательная постановка:
Слайд 57
Математическая модель транспортной задачи
Теорема 3.4.1. (О разрешимости ТЗ)
Для существования
Слайд 60
Методы нахождения начального опорного плана ТЗ.
Опорным планом
Метод северо-западного угла
Слайд 63Проверка плана ТЗ на опорность
(метод вычеркиваний):
вычеркнуть все строки в
более одного положительного элемента;
в получившейся матрице вычеркнуть все столбцы, содержащие не более одного положительного элемента;
далее процесс вычеркивания строк и столбцов применя-
ется к оставшейся подматрице.
Процесс заканчивается одним из двух исходов:
1. Все строки (столбцы) вычеркнуты. Тогда Х − опорный.
2. Получена подматрица, в каждой строке (столбце) которой не менее 2 положительных элементов. Х − не опорный. Из оставшихся элементов можно построить цикл.