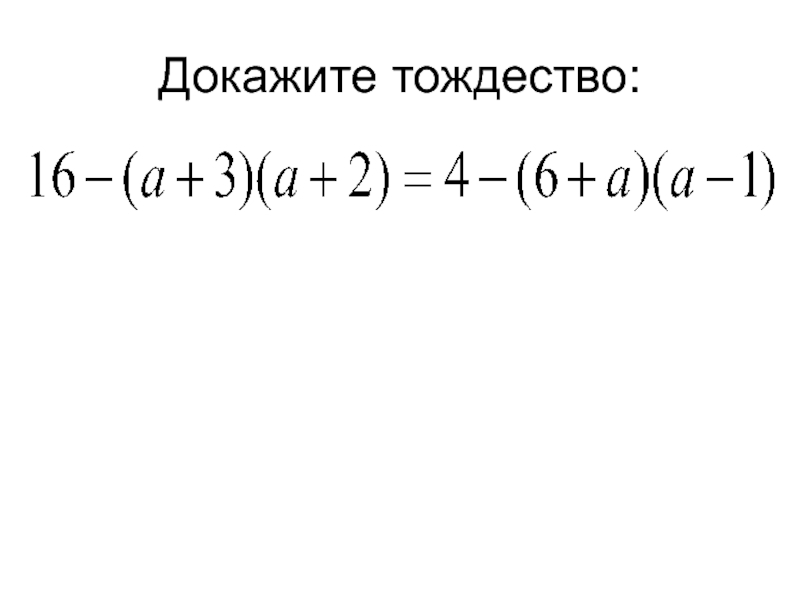- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тождества. Тождественные преобразования выражений. (7 класс) презентация
Содержание
- 1. Тождества. Тождественные преобразования выражений. (7 класс)
- 2. Найдем значение выражений при х=5 и
- 3. ВЫВОД: Мы получили один и тот же
- 4. Рассмотрим теперь выражения 2х+у и 2ху.
- 5. ВЫВОД: Выражения 3(х+у) и 3х+3у являются тождественно
- 6. ТОЖДЕСТВО Равенство 3(х+у) и 3х+3у верно при
- 8. Тождествами являются равенства, выражающие основные свойства действий
- 9. Можно привести и другие примеры тождеств:
- 10. Запомним: ВЫРАЖЕНИЯ, СООТВЕТСВЕННЫЕ ЗНАЧЕНИЯ КОТОРЫХ РАВНЫ ПРИ
- 11. Запиши: Способы доказательства тождеств: Преобразование левой части
- 12. Проверьте, данное выражение – тождество?
- 13. Решение: Преобразуем левую часть равенства:
- 14. Вывод: В результате тождественного преобразования левой части
- 15. В теорию (способы доказательства тождеств): 2.
- 16. Проверьте, данное выражение – тождество?
- 17. Решение: Преобразуем правую часть равенства (а+2)(а+5)=
- 18. Вывод: В результате тождественного преобразования правой части
- 19. В теорию (способы доказательства тождеств): Преобразование обеих частей тождества…..(должны получится одинаковые выражения)
- 20. Докажите тождество:
- 21. Решение: Упростим обе части равенства
- 22. Вывод: Так как левая и правая части
- 23. В теорию (способы доказательства тождеств): 4.
- 24. Докажите тождество: (m-a)(m-b) = m²- (a+b)m + ab
- 26. Вывод: Так как разность между левой
- 27. Работаем по задачнику: № 36.6 (а) - № 36.10 (а)
Найдем значение выражений
при х=5 и у=4
3(х+у)=3(5+4)=3*9=27 3х+3у=3*5+3*4=27 Найдем значение выражений
при х=6 и у=5 3(х+у)=3(6+5)=3*11=33 3х+3у=3*6+3*5=33
Слайд 2Найдем значение выражений
при х=5 и у=4
3(х+у)=3(5+4)=3*9=27
3х+3у=3*5+3*4=27
Найдем значение выражений
при х=6
и у=5
3(х+у)=3(6+5)=3*11=33
3х+3у=3*6+3*5=33
3(х+у)=3(6+5)=3*11=33
3х+3у=3*6+3*5=33
Слайд 3ВЫВОД:
Мы получили один и тот же результат.
Из распределительного свойства следует,
что вообще при любых значениях переменных значения выражений 3(х+у) и 3х+3у равны.
3(х+у) = 3х+3у
3(х+у) = 3х+3у
Слайд 4Рассмотрим теперь выражения 2х+у и 2ху.
при х=1 и у=2 они
принимают равные значения:
2х+у=2*1+2=4
2ху=2*1*2=4
при х=3, у=4 значения выражений разные
2х+у=2*3+4=10
2ху=2*3*4=24
2х+у=2*1+2=4
2ху=2*1*2=4
при х=3, у=4 значения выражений разные
2х+у=2*3+4=10
2ху=2*3*4=24
Слайд 5ВЫВОД:
Выражения 3(х+у) и 3х+3у являются тождественно равными, а выражения 2х+у и
2ху не являются тождественно равными.
Определение:
Два выражения, значения которых равны при любых значениях переменных, называются тождественно равными.
Определение:
Два выражения, значения которых равны при любых значениях переменных, называются тождественно равными.
Слайд 6ТОЖДЕСТВО
Равенство 3(х+у) и 3х+3у верно при любых значениях х и у.
Такие равенства называются тождествами.
Определение: Равенство, верное при любых значениях переменных, называется тождеством.
Тождествами считают и верные числовые равенства. С тождествами мы уже встречались.
Определение: Равенство, верное при любых значениях переменных, называется тождеством.
Тождествами считают и верные числовые равенства. С тождествами мы уже встречались.
Слайд 8Тождествами являются равенства, выражающие основные свойства действий над числами.
a + b
= b + a
ab = ba
(a + b) + c = a + (b + c)
(ab)c = a(bc)
a(b + c) = ab + ac
Слайд 9Можно привести и другие примеры тождеств:
а + 0 = а
а
* 1 = а
а + (-а) = 0
а * (-b) = - ab
а-b = a + (-b)
(-a) * (-b) = ab
а + (-а) = 0
а * (-b) = - ab
а-b = a + (-b)
(-a) * (-b) = ab
Замену одного выражения другим, тождественно равным ему выражением, называют тождественным преобразованием или просто преобразованием выражения.
Слайд 10Запомним:
ВЫРАЖЕНИЯ, СООТВЕТСВЕННЫЕ ЗНАЧЕНИЯ КОТОРЫХ РАВНЫ ПРИ ЛЮБЫХ ДОПУСТИМЫХ ЗНАЧЕНИЯХ ПЕРЕМЕННЫХ, НАЗЫВАЮТСЯ
ТОЖДЕСТВЕННО РАВНЫМИ.
Например: (a²)³ и a6
ab∙(-a²b) и –a³b²
ЗАМЕНУ ОДНОГО ВЫРАЖЕНИЯ ДРУГИМ, ТОЖДЕСТВЕННО РАВНЫМ ЕМУ, НАЗЫВАЮТ ТОЖДЕСТВЕННЫМ ПРЕОБРАЗОВАНИЕМ
Слайд 11Запиши:
Способы доказательства тождеств:
Преобразование левой части тождества так, чтобы получилась её правая
часть
(если после преобразования левой части, выражение получится как в правой части , то данное выражение является тождеством)
(если после преобразования левой части, выражение получится как в правой части , то данное выражение является тождеством)
Слайд 13Решение:
Преобразуем левую часть равенства:
а(в - х) + х(а +
в) =
= ав – ах + ах + хв =
= ав + хв = в(а + х)
= ав – ах + ах + хв =
= ав + хв = в(а + х)
Слайд 14Вывод:
В результате тождественного преобразования левой части равенства, мы получили его
правую
часть и тем самым доказали,
что данное равенство является тождеством.
что данное равенство является тождеством.
Слайд 15В теорию (способы доказательства тождеств):
2. Преобразование правой части тождества так,
чтобы получилась её левая часть
Слайд 18Вывод:
В результате тождественного преобразования правой части равенства, мы получили его левую
часть и тем самым доказали, что данное равенство является тождеством.
Слайд 19В теорию (способы доказательства тождеств):
Преобразование обеих частей тождества…..(должны получится одинаковые выражения)
Слайд 22Вывод:
Так как левая и правая части данного равенства равны одному и
тому же выражению, то они тождественно равны между собой.
Значит исходное равенство –
тождество.
Значит исходное равенство –
тождество.
Слайд 23В теорию (способы доказательства тождеств):
4. Найти разность между правой и левой
частями выражения. (если эта разность равна нулю, то данное выражение - тождество)
Слайд 25
Решение:
(найдем разность между левой и правой частями выражения)
(m-a)(m-b) – [m² - (a+b)m + ab] =
=m² - mb – ma + ab - [m² - am – bm + ab ] =
= m² - mb – ma + ab - m² + am + bm - ab =
= 0
Слайд 26Вывод:
Так как разность между левой и правой частями выражения равна
нулю,
то данное выражения является
тождеством
то данное выражения является
тождеством
