- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Школа олимпийского резерва. (задача) презентация
Содержание
Создадим 3 массива, согласно году рождения Отсортируем каждый из массивов по убыванию баллов Переберем значения M94, M95, M96:
проверяем M94 + M95 + M96 = M и
T94[M94] > T95[M95],
Слайд 2Создадим 3 массива, согласно году рождения
Отсортируем каждый из массивов по убыванию
баллов
Переберем значения M94, M95, M96: проверяем M94 + M95 + M96 = M и T94[M94] > T95[M95], T95[M95] > T96[M96]
T94 Т95 Т96 Ищем минимум
М96 Сложность O(N3)
M94 M95 25 баллов
Переберем значения M94, M95, M96: проверяем M94 + M95 + M96 = M и T94[M94] > T95[M95], T95[M95] > T96[M96]
T94 Т95 Т96 Ищем минимум
М96 Сложность O(N3)
M94 M95 25 баллов
Слайд 3Заметим, что если мы фиксировали значения M94 и M95, то M96
= A + B + C – (M94 + M95), так как
A + B + C = M94 + M95 + M96 = M по условию
Остается проверить, что полученное значение M96 удовлетворяет условиям
1 ≤ M96 ≤ N96, T94[M94] > T95[M95], T95[M95] > T96[M96]
и найти среди таких троек ту, на которой достигается минимум функции
Сложность O(N2) 50 баллов
A + B + C = M94 + M95 + M96 = M по условию
Остается проверить, что полученное значение M96 удовлетворяет условиям
1 ≤ M96 ≤ N96, T94[M94] > T95[M95], T95[M95] > T96[M96]
и найти среди таких троек ту, на которой достигается минимум функции
Сложность O(N2) 50 баллов
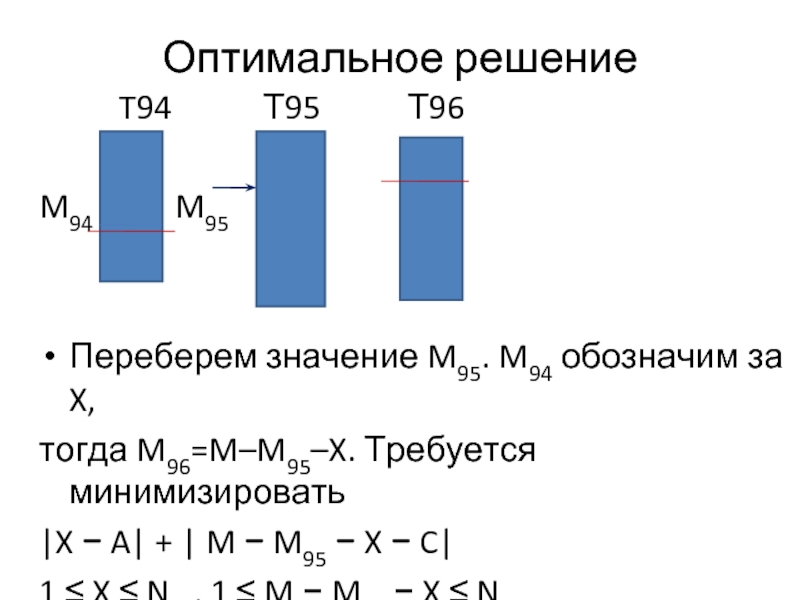
Слайд 4Оптимальное решение
T94 Т95
Т96
М96
M94 M95
Переберем значение M95. M94 обозначим за X,
тогда M96=M–M95–X. Требуется минимизировать
|X − A| + | M − M95 − X − C|
1 ≤ X ≤ N94, 1 ≤ M − M95 − X ≤ N96
М96
M94 M95
Переберем значение M95. M94 обозначим за X,
тогда M96=M–M95–X. Требуется минимизировать
|X − A| + | M − M95 − X − C|
1 ≤ X ≤ N94, 1 ≤ M − M95 − X ≤ N96
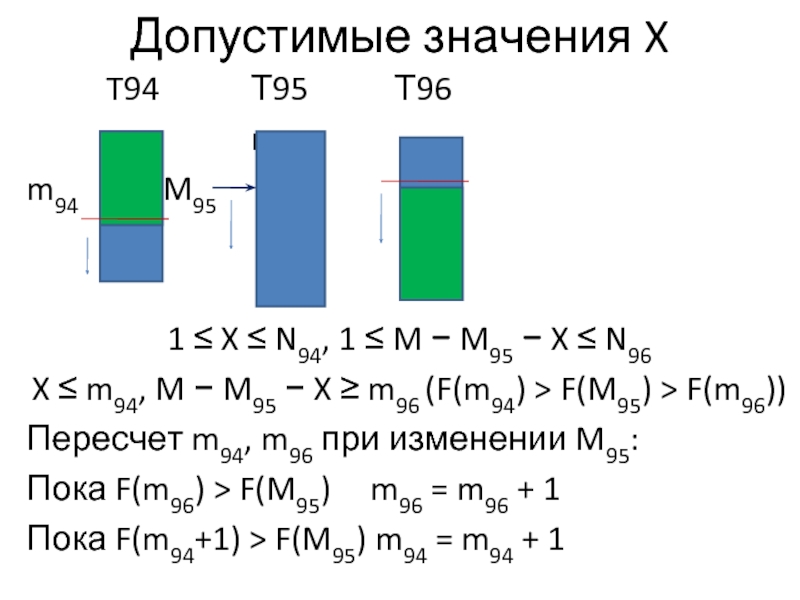
Слайд 5Допустимые значения X
T94 Т95
Т96
m96
m94 M95
1 ≤ X ≤ N94, 1 ≤ M − M95 − X ≤ N96
X ≤ m94, M − M95 − X ≥ m96 (F(m94) > F(M95) > F(m96))
Пересчет m94, m96 при изменении M95:
Пока F(m96) > F(M95) m96 = m96 + 1
Пока F(m94+1) > F(M95) m94 = m94 + 1
m96
m94 M95
1 ≤ X ≤ N94, 1 ≤ M − M95 − X ≤ N96
X ≤ m94, M − M95 − X ≥ m96 (F(m94) > F(M95) > F(m96))
Пересчет m94, m96 при изменении M95:
Пока F(m96) > F(M95) m96 = m96 + 1
Пока F(m94+1) > F(M95) m94 = m94 + 1
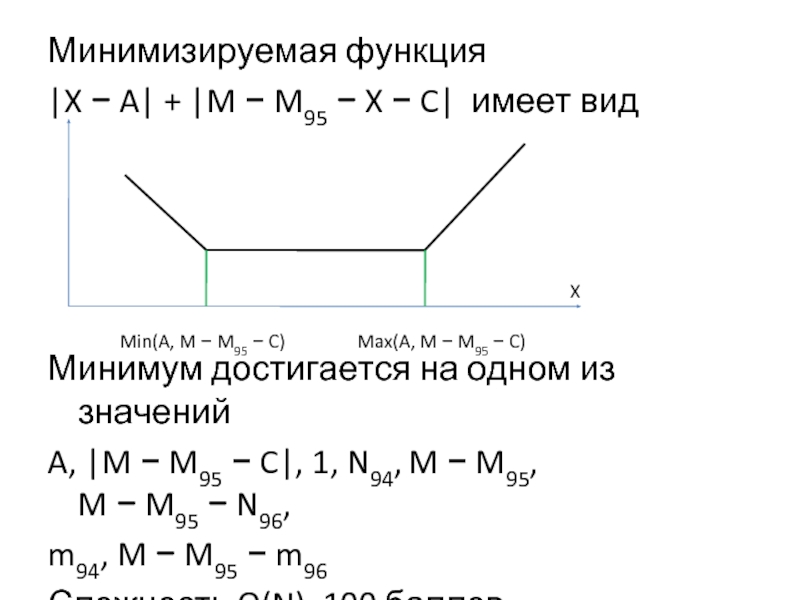
Слайд 6Минимизируемая функция
|X − A| + |M − M95 − X − C| имеет вид
Минимум достигается на одном из значений
A, |M − M95 − C|, 1,
N94, M − M95, M − M95 − N96,
m94, M − M95 − m96
Сложность O(N), 100 баллов
m94, M − M95 − m96
Сложность O(N), 100 баллов
Min(A, M − M95 − C)
Max(A, M − M95 − C)
X
