- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Аттестационная работа. Метод рационализации применим к решению неравенств, систем неравенств на ЕГЭ презентация
Содержание
- 1. Аттестационная работа. Метод рационализации применим к решению неравенств, систем неравенств на ЕГЭ
- 2. Гипотеза Метод рационализации применим к решению неравенств
- 3. Задачи: 1. Изучить книжную литературу и Интернет-ресурсы
- 4. Методы исследования: Изучение литературы (научной и Интернет-ресурсов)
- 5. Актуальность Тема решения неравенств методом рационализации является
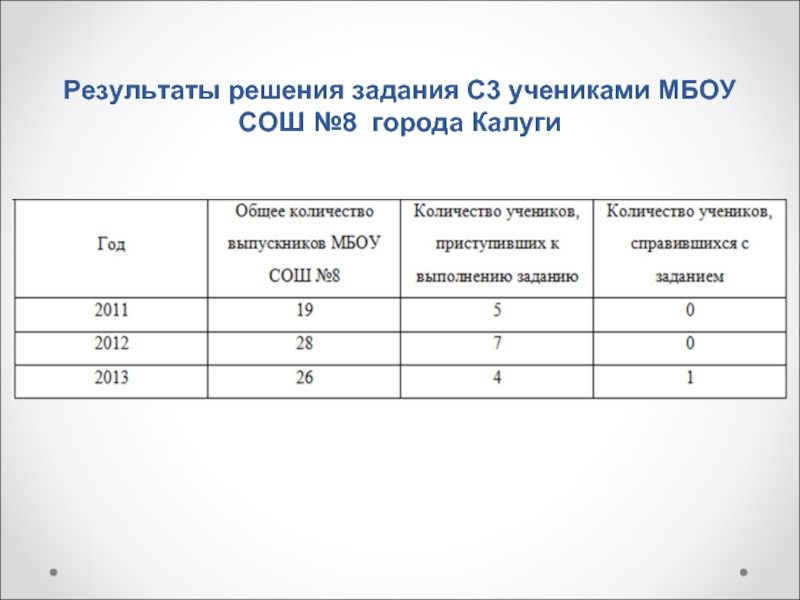
- 6. Результаты решения задания С3 учениками МБОУ СОШ №8 города Калуги
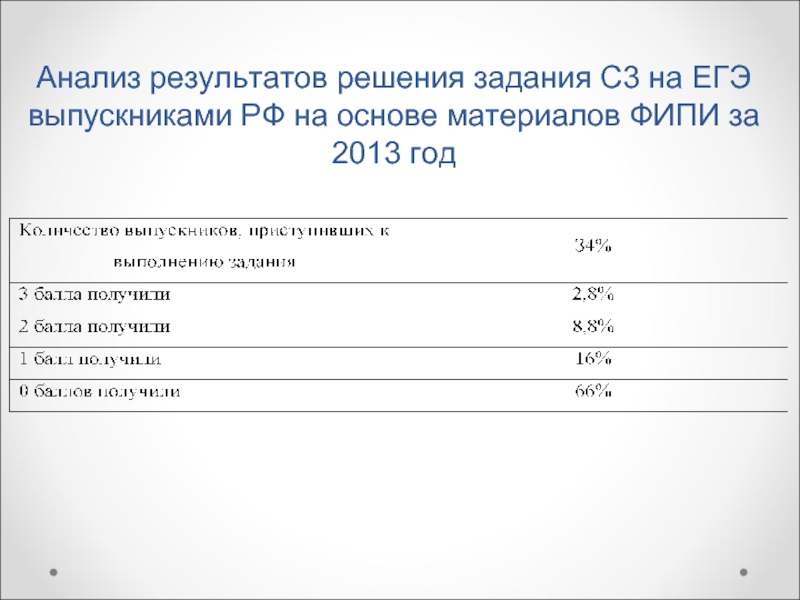
- 7. Анализ результатов решения задания С3 на ЕГЭ
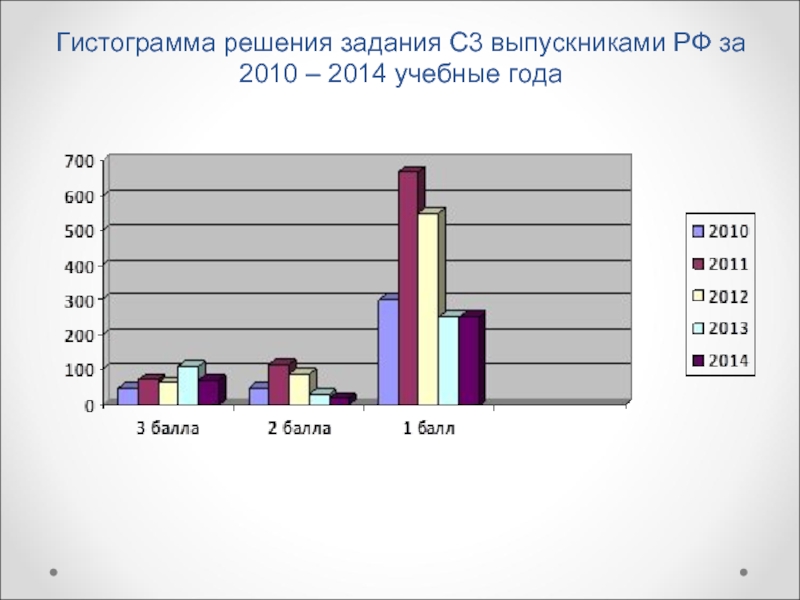
- 8. Гистограмма решения задания С3 выпускниками РФ за 2010 – 2014 учебные года
- 9. Таблица перехода иррациональных и трансцендентных выражений к рациональным
- 10. Алгоритм метода рационализации Выписать условия, задающие ОДЗ
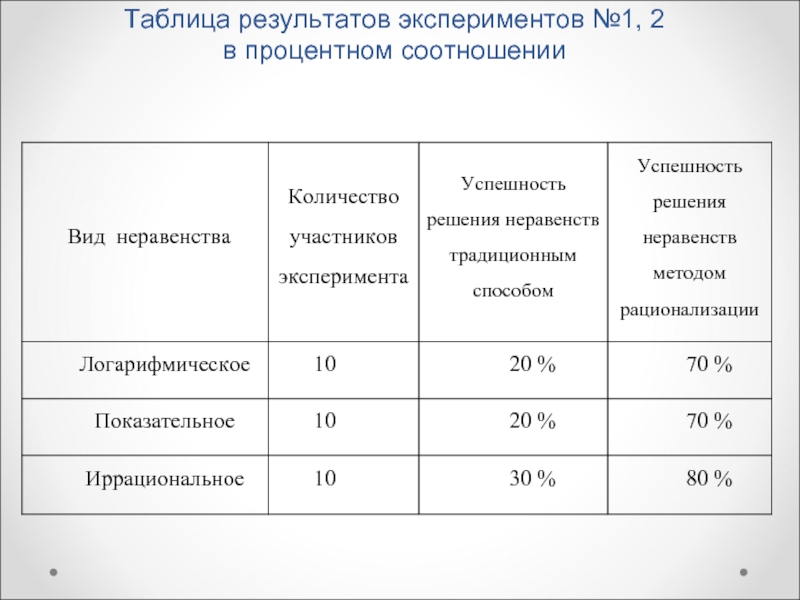
- 11. Таблица экспериментов №1, 2
Слайд 1Использование Метода рационализации при решении неравенств на Едином государственном экзамене
Слайд 2Гипотеза
Метод рационализации применим к решению неравенств (систем неравенств) на ЕГЭ.
Цель работы
Практически
оценить метод рационализации при решении иррациональных, логарифмических и показательных неравенств, выявив значимость данного метода с точки зрения экономии времени и объема решения.
Слайд 3Задачи:
1. Изучить книжную литературу и Интернет-ресурсы по проблеме исследования.
2. Обработать и
систематизировать информацию по поднятой теме.
3. Передать накопленный опыт учащимся 11 класса МБОУ «Средняя общеобразовательная школа №8» г. Калуги.
3. Передать накопленный опыт учащимся 11 класса МБОУ «Средняя общеобразовательная школа №8» г. Калуги.
Слайд 4Методы исследования:
Изучение литературы (научной и Интернет-ресурсов)
2. Опрос (выпускников школы и учителей
математики)
3. Работа в архивах (с документами, содержащими статистические данные о решаемости тех или иных заданий ЕГЭ учениками)
4. Практические занятия (среди учащихся 11 класса МБОУ СОШ №8)
5. Анализ результатов по проблеме исследования.
3. Работа в архивах (с документами, содержащими статистические данные о решаемости тех или иных заданий ЕГЭ учениками)
4. Практические занятия (среди учащихся 11 класса МБОУ СОШ №8)
5. Анализ результатов по проблеме исследования.
Слайд 5Актуальность
Тема решения неравенств методом рационализации является актуальной, т. к. ее изучение
может быть полезно учащимся школ (преимущественно выпускникам) и педагогам как несколько иной способ решения неравенств.
Новизна
Новизна работы заключается в том,
что несмотря на довольно долгую известность данного метода решения неравенств (систем неравенств), в школьной программе он не изложен, следовательно, не известен ученикам.
Новизна
Новизна работы заключается в том,
что несмотря на довольно долгую известность данного метода решения неравенств (систем неравенств), в школьной программе он не изложен, следовательно, не известен ученикам.
Слайд 7Анализ результатов решения задания С3 на ЕГЭ выпускниками РФ на основе
материалов ФИПИ за 2013 год
Слайд 10Алгоритм метода рационализации
Выписать условия, задающие ОДЗ исходного неравенства.
Привести исходное неравенство к
стандартному виду.
Указать область допустимых значений для получившегося неравенства.
Заменить все выражения на рациональные (используя специальную таблицу перехода к рациональным выражениям).
Решить полученное неравенство. (Например, методом интервалов.)
6. Записать ответ полученного неравенства (он же является ответом исходного неравенства).
Указать область допустимых значений для получившегося неравенства.
Заменить все выражения на рациональные (используя специальную таблицу перехода к рациональным выражениям).
Решить полученное неравенство. (Например, методом интервалов.)
6. Записать ответ полученного неравенства (он же является ответом исходного неравенства).