Лекции- 26 часов
Практические занятия- 26 часов
Экзамен, зачет.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория вероятностей, математическая статистика и случанйные процессы презентация
Содержание
- 1. Теория вероятностей, математическая статистика и случанйные процессы
- 2. Литература 1 .Гмурман
- 3. Пространство элементарных событий Ω Пространством элементарных событий
- 4. Случайные события Случайным событием или просто событием
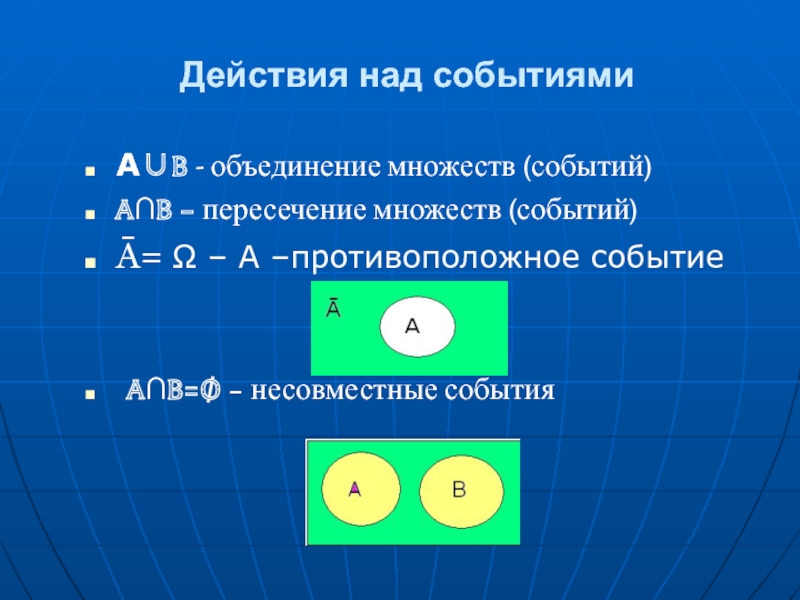
- 5. Действия над событиями A∪B - объединение множеств
- 6. Комбинаторика Основное правило комбинаторики: пусть требуется совершить
- 7. Сочетания: Перестановки:
- 8. Вероятность Аксиоматическое определение вероятности: Вероятность на
- 9. Классическая вероятность:
- 10. Вероятность суммы вероятность суммы для совместных событий
- 11. Условная вероятность Условная вероятность для
- 12. Вероятность произведения Вероятность произведения двух событий равна
- 13. Формула полной вероятности
- 14. Формула Байеса
- 15. Испытания Бернулли Производится последовательность независимых испытаний, в
- 16. Случайная величина Случайная величина ξ
- 17. Случайная величина дискретного типа Закон задается в
- 18. Функция распределения F(x)=P(ξ
- 19. Свойства функции распределения F(-∞)=0; F(∞)=1; F(x)-неубывающая функция; х1
- 20. Случайная величина непрерывного типа
- 21. Плотность вероятностей Плотность распределения
- 22. Свойства плотности вероятностей График плотности вероятностей f(x)
- 23. Числовые характеристики случайных величин Математическое
- 24. Свойства математического ожилания 1 Математическое ожидание постоянной
- 25. Дисперсия случайной величины Дисперсией случайной величины ξ
- 26. Для дискретной ξ:
- 27. Свойства дисперсии 1 Дисперсия положительная величина
- 28. 4 Дисперсия суммы и разности независимых
- 29. Моменты Начальный момент К порядка:
- 30. Центральный момент К порядка:
- 31. Квантиль Квантиль порядка Р для распределения F(x)
- 32. Типовые законы распределения случайных величин Биномиальный закон:
- 33. Целочисленная случайная величина ξ подчинена биномиальному
- 34. Закон Пуассона ξ – дискретная случайная величина,
- 35. Равномерное распределение Непрерывная случайная величина ξ распределена
- 36. Функция распределения
- 37. Закон экспоненциального распределения Непрерывная случайная величина ξ
- 38. Функция распределения Математическое
- 39. Закон нормального распределения (закон Гаусса) Плотность вероятностей:
- 40. Интеграл вероятностей
- 41. Локальная теорема Муавра-Лапласа При неограниченном увеличении числа
- 42. Интегральная теорема Муавра-Лапласа При неограниченном увеличении
- 43. Системы случайных величин Совокупность нескольких случайных величин,
- 44. Законы распределения системы Таблица распределения является формой
- 45. Функция распределения системы F(x,y)=P(ξ
- 46. Плотность системы случайных величин
- 47. Вероятность попадания системы в область D:
- 48. Дисперсия системы Дисперсия системы определяется по
- 49. Корреляционный момент Корреляционный момент есть
- 50. Для непрерывной системы: х,у
- 51. Свойства корреляционного момента Корреляционный момент симметричен:
- 52. Коэффициент корреляции Наличие размерности
- 53. Коэффициент корреляции обладает свойствами
- 54. Условное математическое ожидание; линейная регрессия Для дискретной
- 55. В практике функция регрессии относится
Слайд 1 ШАЛАЕВ Ю.Н. доцент каф. ИПС, АВТФ ТЕОРИЯ ВЕРОЯТНОСТЕЙ, МАТЕМАТИЧЕСКАЯ СТАТИСТИКА И СЛУЧАНЙНЫЕ
Слайд 2Литература
1 .Гмурман В.Е. Курс теории вероятностей. М.: В.Ш.
2. Вентцель Е. С. Теория вероятностей М.: Наука, 1979,2000.
3. Чистяков В.П. Курс теории вероятностей. М.:1987.
Свешников А.А. Сборник задач по теории вероятностей, математической статистике и теории случайных функций. М.: Наука, 1965.
Слайд 3Пространство элементарных событий Ω
Пространством элементарных событий Ω
называется множество элементарных
событий ωi ,
Слайд 4Случайные события
Случайным событием или просто
событием называется подмножество А
множества Ω:
Для дискретного Ω число случайных событий N=2n.
Слайд 5Действия над событиями
A∪B - объединение множеств (событий)
A∩B – пересечение множеств (событий)
Ā=
A∩B=Ø – несовместные события
Слайд 6Комбинаторика
Основное правило комбинаторики:
пусть требуется совершить одно за другим К действий и
N=n1·n2···nk
способами.
Слайд 8Вероятность
Аксиоматическое определение вероятности:
Вероятность на пространстве элементарных
событий Ω называется функция Р(А),
обладающая
Слайд 9Классическая вероятность:
Геометрическая вероятность: Р(А)=LA/LΩ; Р(А)=SA/SΩ; Р(А)=VA/VΩ, где L-длина, S-площадь, V-объем.
Статистическая вероятность:
Р(А)=limnA/n. n-∞
Слайд 10Вероятность суммы
вероятность суммы для совместных событий А и В определяется по
Р(А U В) = Р(А) + Р(В) – Р(А ∩ В);
Вероятность противоположного события
Р(Ā)=1-Р(А)
Слайд 11Условная вероятность
Условная вероятность для зависимых событий определяется по соотношению
События А и В независимы, если условная вероятность равна своей безусловной вероятности
Р(А/В) = Р(А);
Слайд 12Вероятность произведения
Вероятность произведения двух событий равна произведению вероятностей одного из этих
Для трех событий:
Р(А∩В∩С)=Р(А)·Р(В/А)·Р(С/АВ);
для независимых событий вероятность произведения равна произведению вероятностей Р(А ∩ В) = Р(А) Р(В);
Вероятность произведения коммутативна:
Р(А∩В)=Р(А)·Р(В/А);
Р(А∩В)=Р(В)·Р(А/В).
Слайд 13Формула полной вероятности
А-произвольное событие;
События Н1, Н2,…Нn попарно
Слайд 15Испытания Бернулли
Производится последовательность независимых испытаний, в каждом из которых с постоянной
Слайд 16Случайная величина
Случайная величина ξ это действительная функция
Т.е. случайная величина-это функция; аргумент у которой, элементарное событие; значение-число.
Случайные события (А,В,…) качественные характеристики случайных явлений. Случайная величина дает количественную характеристику явлений.
Слайд 17Случайная величина дискретного типа
Закон задается в виде ряда распределения-это совокупность пар
Слайд 18Функция распределения
Функция распределения неслучайная функция; аргумент-вещественное х; значение-число.
Слайд 19Свойства функции распределения
F(-∞)=0; F(∞)=1;
F(x)-неубывающая функция; х1
P(а≤ξ<в)= F(в) – F(а)
Слайд 20Случайная величина непрерывного типа
f(x) – плотность распределения вероятностей случайной величины ξ.
Слайд 21Плотность вероятностей
Плотность распределения вероятностей случайной
величины ξ, называется предел
длине этого интервала:
Если этот предел существует, то он равен производной
от функции распределения
Слайд 22Свойства плотности вероятностей
График плотности вероятностей f(x) – кривая распределения вероятностей;
Плотность вероятностей
Плотность вероятностей нормирована на единицу:
Вероятность попадания на интервал [а,в):
Слайд 23Числовые характеристики случайных величин
Математическое ожидание –
это число, которое характеризует
Для непрерывной ξ:
Слайд 24Свойства математического ожилания
1 Математическое ожидание постоянной величины С равно
самой
2 Постоянную величину можно выносить за оператор
математического ожидания: МСξ=СМξ;
3 Математическое ожидание суммы случайных величин
равно сумме математических ожиданий этих величин:
М(ξ + η)=Мξ + Мη :
4 Математическое ожидание произведения независимых случайных
величин равно произведению математическое ожиданий
этих величин: Мξη=Мξ*Мη.
Слайд 25Дисперсия случайной величины
Дисперсией случайной величины ξ называется число
Которое является мерой рассеяния случайной значений
величины около ее математического ожидания.
После преобразования правой части получим второе
соотношение для дисперсии:
Dξ=Mξ2 – (Mξ)2.
Слайд 27Свойства дисперсии
1 Дисперсия положительная величина
2 Дисперсия постоянной величины равна нулю: DC=0;
3 Константу можно выносить за оператор дисперсии в
квадрате
DCξ=C2Dξ;
Слайд 28
4 Дисперсия суммы и разности независимых случайных величин равна сумме дисперсий
D(ξ+η)=Dξ+Dη;
D(ξ-η)=Dξ+Dη;
5 Среднее квадратическое отклонение:
6 Дисперсия показывает средний квадрат разброса случайной величины относительно центра (математического ожидания).
Слайд 30
Центральный момент К порядка:
μк=М(ξ-Мξ)к, μ1=0,
Для дискретной ξ: Для непрерывной ξ:
Слайд 31Квантиль
Квантиль порядка Р для распределения F(x)
называется значение εР для которого
F(εР )=P.
Слайд 32Типовые законы распределения случайных величин
Биномиальный закон:
Проводится серия из “n”однородных и независимых
ξ=k; k=0,1,2,…, “n” .
Слайд 33
Целочисленная случайная величина ξ подчинена биномиальному закону, если вероятности ряда распределения
Дисперсия: D ξ=npq.
Слайд 34Закон Пуассона
ξ – дискретная случайная величина, которая принимает целые неотрицательные значения:
Математическое ожидание Mξ=a;
Дисперсия Dξ=a.
Слайд 35Равномерное распределение
Непрерывная случайная величина ξ распределена по равномерному закону, если плотность
Слайд 37Закон экспоненциального распределения
Непрерывная случайная величина ξ распределена по экспоненциальному закону, если
Слайд 39Закон нормального распределения
(закон Гаусса)
Плотность вероятностей:
Функция распределения:
Математическое ожидание: Мξ=а;
Дисперсия:
Слайд 40Интеграл вероятностей
Интеграл вероятностей есть функция распределения Гауссовской случайной величины Z:
Слайд 41Локальная теорема Муавра-Лапласа
При неограниченном увеличении числа испытаний “n” формула Бернулли сводится
Формула справедлива для всех 0<р<1 и 0≤k≤n.
Слайд 42Интегральная теорема Муавра-Лапласа
При неограниченном увеличении числа испытаний “n”
вероятность попадания случайной
Слайд 43Системы случайных величин
Совокупность нескольких случайных величин, рассматриваемых совместно называется системой случайных
Слайд 44Законы распределения системы
Таблица распределения является формой записи закона распределения системы дискретной
Pij=P(ξ=xi, η=yj);
Слайд 45Функция распределения системы
Слайд 46Плотность системы случайных величин
Свойства плотности вероятностей системы
1 Плотность
Слайд 48Дисперсия системы
Дисперсия системы определяется по законам отдельных составляющих системы:
Среднее квадратическое отклонение характеризует рассеивание системы относительно центра (математического ожидания).
Слайд 49Корреляционный момент
Корреляционный момент есть математическое ожидание центрированной системы:
Слайд 50Для непрерывной системы:
х,у – возможные значения ξ, η;
f(x,y) – плотность вероятностей
Геометрически Кξη показывает величину отклонения системы от центра. Если Кξη ≠0, то система коррелированна. Если Кξη =0, то система не коррелированна. Из независимости системы вытекает некоррелированность, обратное может быть и неверно.
Слайд 51Свойства корреляционного момента
Корреляционный момент симметричен:
Кξξ = Dξ; Кξξ = M(x-Mξ)(x-Mξ)=Dξ;
Kηη= Dη; Kηη= M(y-Mη)(y-Mη)=Dη;
Совокупность всех корреляционных моментов, расположенных в квадратной таблице называется корреляционной матрицей системы:
Слайд 52Коэффициент корреляции
Наличие размерности у корреляционного момента вызывает неудобства, поэтому
Слайд 53
Коэффициент корреляции обладает свойствами корреляционного момента:
показывает меру линейной связи
rξη = 0, если ξ,η некоррелированные случайные величины;
коэффициент корреляции системы симметричен: rξη = rηξ;
/ rξη /≤1; (1 – максимальное значение);
Совокупность всех коэффициентов корреляции в виде таблице образуют нормированную корреляционную матрицу системы:
Слайд 54Условное математическое ожидание;
линейная регрессия
Для дискретной ξ:
Для непрерывной ξ :
Функция регрессии показывает
Слайд 55
В практике функция регрессии относится к линейной:
Коэффициенты регрессии подбирают так, чтобы обеспечить минимум среднего разброса η относительно прямой регрессии (метод наименьших квадратов): вводится уклонение η относительно прямой регрессии: Δ = (у – (β0 + β1х)):
находим дисперсию:
Δ2(β0, β1) = М(у – (β0 + β1х)) 2 min→ β0, β1 : после преобразования получим:
φ(х)=β0 + β1х = Мη + rξη∙ση/σξ∙(x - Mξ).