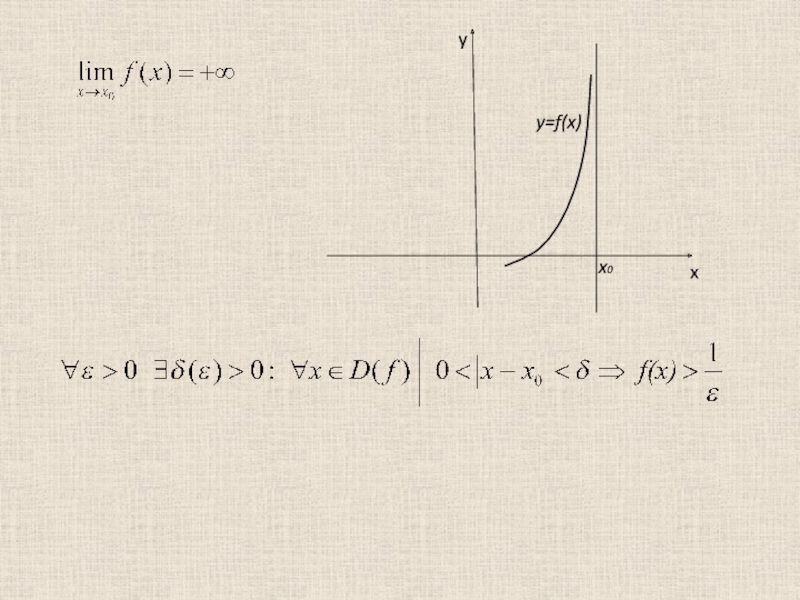- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория пределов презентация
Содержание
- 1. Теория пределов
- 2. Числовая последовательность 1 2 3 4 … n… 2 4 8 16 … 2ⁿ… а1 а2 а3 а4 … аn…
- 3. Предел числовой последовательности 0 1
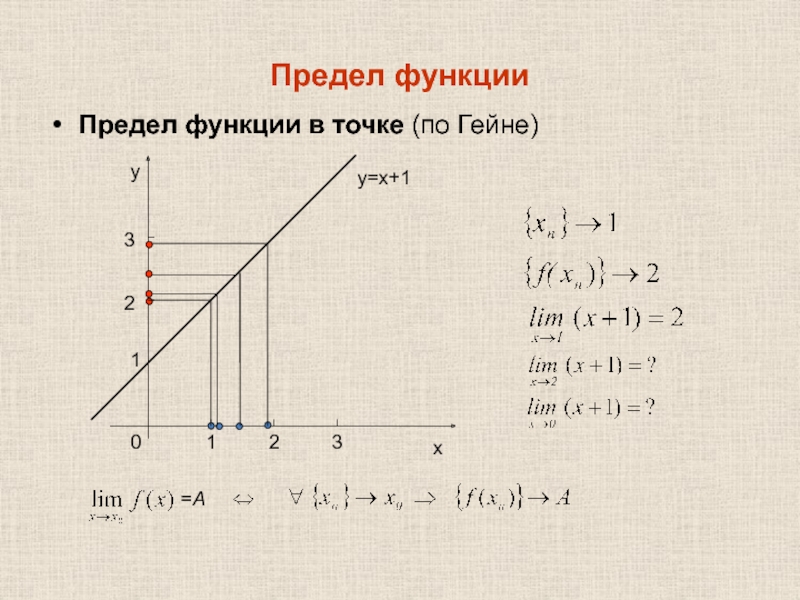
- 4. Предел функции Предел функции в точке (по
- 5. Предел функции в точке (по Коши)
- 6. Бесконечные пределы х у А y=f(x) х у А y=f(x)
- 8. Бесконечно малые и бесконечно большие функции
- 9. Теорема о связи между функцией и ее
- 10. Теорема о связи бесконечно малой и бесконечно
- 11. Свойства бесконечно малых функций
- 12. Свойства бесконечно больших функций
- 13. Сравнение бесконечно малых функций Пусть α(х) и
- 14. Свойства эквивалентных бесконечно малых 1. α ~ β
- 15. Основные теоремы о пределах О пределе постоянной.
- 16. Теорема об арифметике
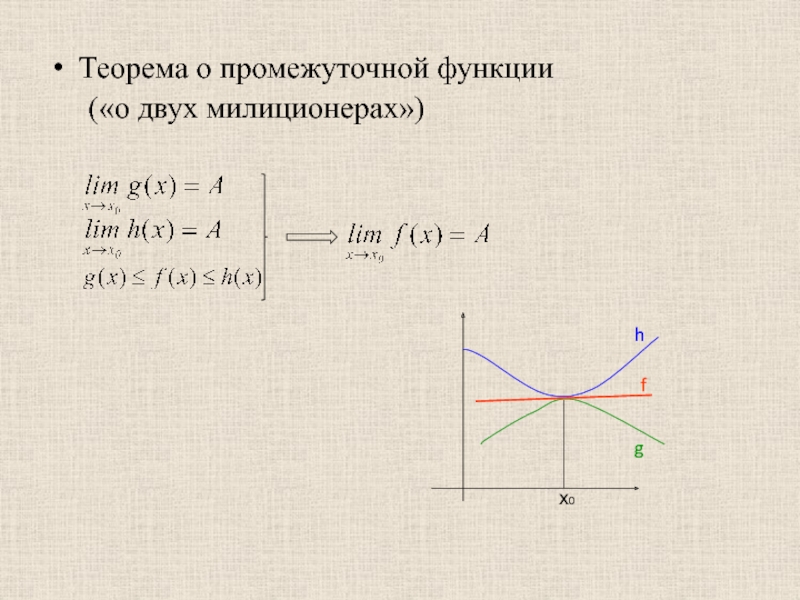
- 17. Теорема о промежуточной функции («о двух
- 18. Предел отношения синуса бесконечно малой дуги к
- 19. Вопросы к семинару 2. Числовая последовательность и
- 20. Техника вычисления пределов . Найти пределы
Слайд 2Числовая последовательность
1 2 3 4 … n…
2 4 8 16 … 2ⁿ…
а1 а2 а3 а4 … аn…
-аргумент
-члены последовательности
: 1/2, 1/3, 1/4, ….
Слайд 8Бесконечно малые
и бесконечно большие функции
- бесконечно малая при
, если
-
, если
х
у
0
y=x²
Слайд 9Теорема о связи между функцией и ее пределом
Если функция при х→х0
равный А, то разность между функцией и значением ее предела бесконечно мала при х→х0 :
Слайд 10Теорема о связи бесконечно малой и бесконечно большой функций
- бесконечно малая
Если
и
в некоторой окрестности точки х0 , то
является бесконечно большой при
функция
- бесконечно большая при
Если
является бесконечно малой при
то функция
Слайд 13Сравнение бесконечно малых функций
Пусть α(х) и β(х) – бесконечно малые при
А≠0, А≠1: α и β – бесконечно малые одинакового порядка;
А=0: α – более высокого порядка малости,
А=±∞: β – более высокого порядка малости;
А=1: α и β – эквивалентные бесконечно малые, α~β.
Слайд 14Свойства эквивалентных бесконечно малых
1. α ~ β ↔ β ~ α (рефлексивность)
2.
3. α ~ β → α = β +o(α) (эквивалентные бесконечно малые отличаются друг от друга на бесконечно малую высшего порядка).
4. Под знаком предела в отношении или произведении бесконечно малые можно заменять эквивалентными.
Слайд 15Основные теоремы о пределах
О пределе постоянной.
О единственности предела.
Необходимые условия существования конечного
3. О локальной ограниченности.
4. О локальном повторении функцией свойств предела.
Достаточные условия существования конечного предела:
5. Об арифметике.
6. О промежуточной функции.
7. О пределе монотонной ограниченной функции.
Слайд 18Предел отношения синуса бесконечно малой дуги к самой дуге (в радианах)
Следствия:
Числовая последовательность
имеет конечный предел, равный е:
Следствия:
Замечательные пределы
Слайд 19Вопросы к семинару 2.
Числовая последовательность и ее предел.
Предел функции в точке:
Односторонние пределы.
Бесконечные пределы.
Бесконечно малые и бесконечно большие функции, их свойства.
Теорема о связи между функцией и ее пределом.
Теорема о связи бесконечно малой и бесконечно большой функций.
Сравнение бесконечно малых функций.
Свойства бесконечно малых функций.
Основные теоремы о пределах: о пределе постоянной, о единственности предела, о локальной ограниченности, о локальном повторении функцией свойств предела, об арифметике, о промежуточной функции, о пределе монотонной ограниченной функции.
Замечательные пределы.