- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория Множеств презентация
Содержание
- 1. Теория Множеств
- 2. Введение в теорию множеств 1. Основные определения,
- 3. Следует отметить, что объект а и множество
- 4. Определение 1 Множество А называется подмножеством В,
- 5. N ⊂ Z ⊂ Q ⊂ R
- 6. Определение 2 Множества А и В называются
- 7. Равенство множеств Если А В
- 8. Определение 3 Множество называется пустым, если оно
- 9. 2. Операции над множествами Определение 1 Объединением
- 10. Объединение множеств Теорема 1 Пусть А, В,
- 11. Пересечение множеств Определение 2 Пересечением множеств А
- 12. Теорема 2 Пусть А, В, С – произвольные
- 13. Объединение и пересечение множеств Теорема 3 1)
- 14. Разность множеств, дополнение, симметрическая разность Определение
- 15. Разность множеств Теорема 4 Пусть А,
- 17. Дополнение множеств Определение 4 Пусть U – универсальное
- 18. Дополнение множеств 1) 2) 3)
- 19. Симметрическая разность Определение 5 Симметрической разностью множеств
- 20. Спасибо за внимание!!!
- 21. Равна ли часть целому? Основная догма, которую
- 22. Трудно примериться, что дорога в миллион световых
- 23. Любой отрезок [a, b] , эквивалентен отрезку
- 24. Тайны бесконечности Математики и философы всегда интересовались
- 25. Конечные множества Множество называется конечным ,если оно
- 26. Задачи Из 100 туристов, отправляющихся в заграничное
- 27. Задание 1. Найдите объединение и пересечение множеств
Слайд 2Введение в теорию множеств
1. Основные определения, терминология
Под множеством А мы
Обозначение
Указанием определяющего свойства
Перечислением элементов
Пример 1
Иногда второе обозначение распространяется и на некоторые бесконечные множества. Так,
N={1,2,3,...,n,...}
Z={...,-n,...,-2,-1,0,1,2,...,n,...}.
Слайд 3Следует отметить, что объект а и множество {а} - это различные
первое - это объект, обозначенный через а, второе-это множество, состоящее из (единственного) объекта а.
Другая форма обозначения состоит в указании общего свойства объектов, из которых мы образуем множество. Оно имеет вид: M={x | P (x) }
Читается: “множество всех х таких, что Р (х)” , где Р обозначает свойство, характеризующее в точности все элементы данного множества.
Например
{x | x- целое число, делящееся на 2} - означает множество четных чисел
Слайд 4Определение 1
Множество А называется подмножеством В, если для любого х (
Обозначение:
Другими словами, символ " " есть сокращение для высказывания Теорема 1
Для любых множеств А, В, С верно следующее:
а) ;
б) и .
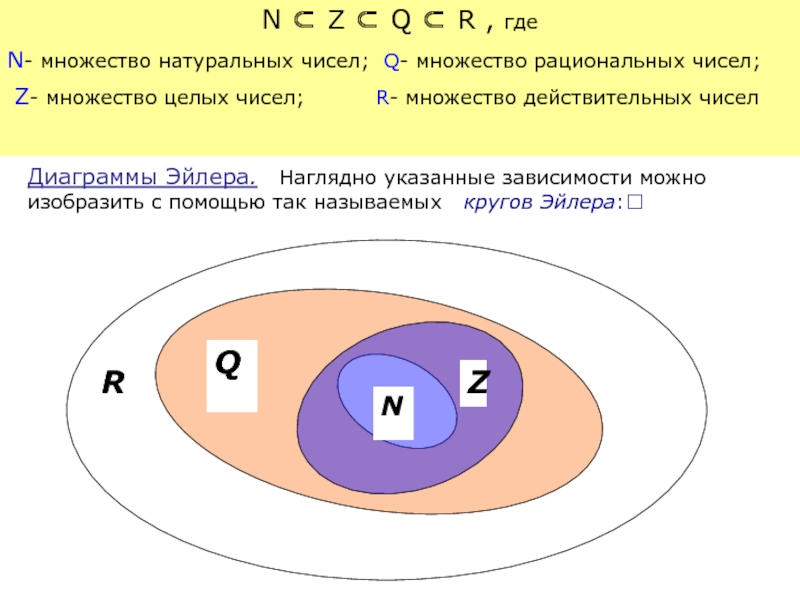
Слайд 5N ⊂ Z ⊂ Q ⊂ R , где
N- множество
Z- множество целых чисел; R- множество действительных чисел
Z
N
R
Q
Диаграммы Эйлера. Наглядно указанные зависимости можно изобразить с помощью так называемых кругов Эйлера:
Слайд 6Определение 2
Множества А и В называются равными, если они состоят из
Пример
Указать равные множества
A={0;1;2}, B = {1;0;2}, C={0;1;2;0}, D={{1;2};0}, E={1;2}, F={x:x3-3x2+2x=0}.
Слайд 7Равенство множеств
Если А В и В А
называют равными и обозначают: А=В.
Даны множества:
А - множество целых чисел;
В - множество четных чисел;
С - множество нечетных чисел;
D - множество чисел, кратных 3;
Е- множество чисел, кратных 6;
Т - множество чисел, оканчивающихся цифрой 0;
К - множество чисел, которые при делении на 8 дают в остатке 5;
F - множество чисел, кратных 2 и 3 одновременно; М - множество чисел, кратных 2 и 5 одновременно.
Имеются ли среди данных множеств равные множества?
Слайд 8Определение 3
Множество называется пустым, если оно не содержит ни одного элемента,
Слайд 92. Операции над множествами
Определение 1
Объединением двух множеств А и В называется
Пример
Пусть А={1,2,3,4}, B={2,4,6,8}, тогда = {1,2,3,4,6,8}.
A
B
Слайд 10Объединение множеств
Теорема 1
Пусть А, В, С – произвольные множества. Тогда:
а)
б) – коммутативность объединения;
в) – ассоциативность объединения;
г) ;
д)
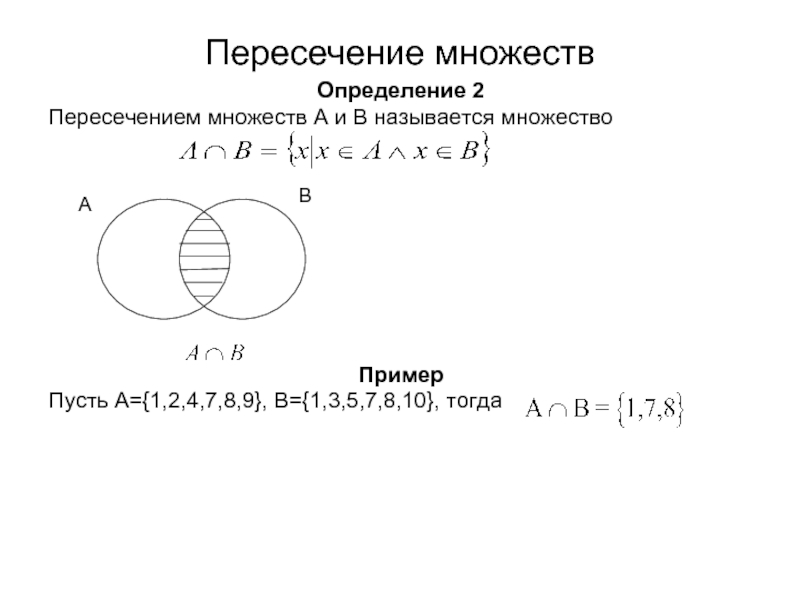
Слайд 11Пересечение множеств
Определение 2
Пересечением множеств А и В называется множество
Пример
Пусть A={1,2,4,7,8,9}, B={1,3,5,7,8,10}, тогда
A
B
Слайд 12Теорема 2
Пусть А, В, С – произвольные множества, тогда:
а)
б) - коммутативность пересечения;
в) - ассоциативность пересечения;
г)
Пересечение множеств
Слайд 14 Разность множеств, дополнение, симметрическая разность
Определение 3
Разностью множеств A и B
.
Пример
Пусть А={1,3,4,7,8,9,10}, B={2,3,4,5,6,7}, тогда A\B={1,8,9,10}, B\A={2,5,6}.
A
B
Слайд 15Разность множеств
Теорема 4
Пусть А, В, С – произвольные множества, тогда:
1)
2)
3)
4)
Теорема 5 (законы
а)
б)
Слайд 16
Множество U назовем "универсальным", если оно содержит все элементы и все множества являются его подмножествами. Понятие "универсального множества" у нас будет зависеть от круга задач, которые мы рассматриваем. Довольно часто под универсальным множеством понимают множество R –– множество вещественных чисел или множество С – комплексных чисел. Возможны и другие примеры. Всегда в контексте необходимо оговорить, что мы понимаем под универсальным множеством U.
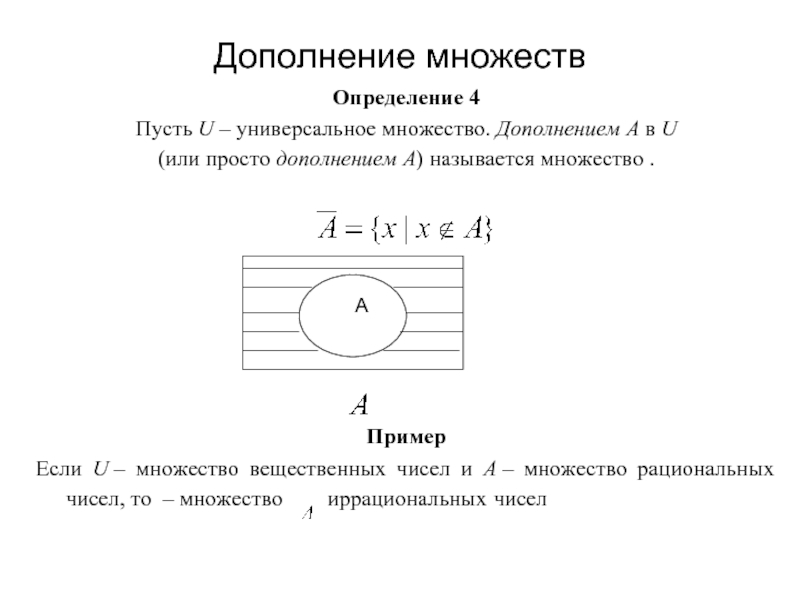
Слайд 17Дополнение множеств
Определение 4
Пусть U – универсальное множество. Дополнением А в U
(или
Пример
Если U – множество вещественных чисел и А – множество рациональных чисел, то – множество иррациональных чисел
A
Слайд 19Симметрическая разность
Определение 5
Симметрической разностью множеств A и B называют множество
Задача (3
Доказать, что
A
B
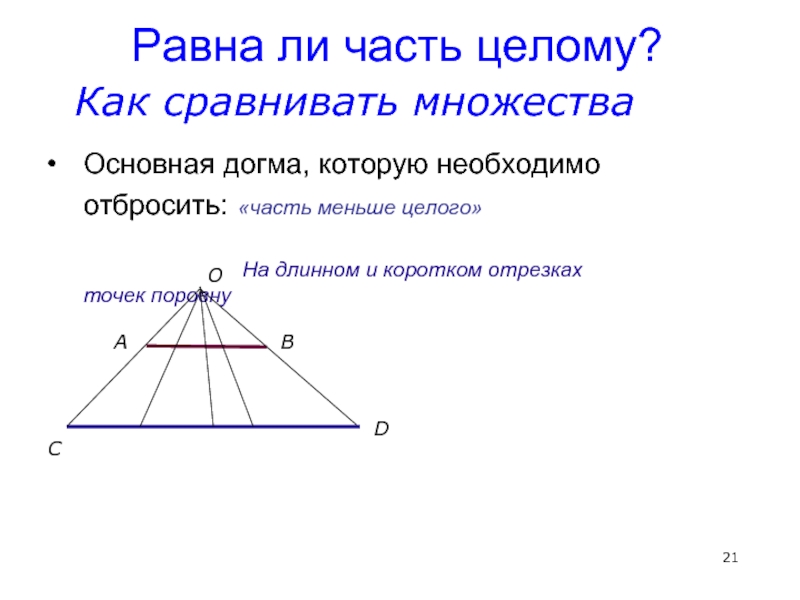
Слайд 21Равна ли часть целому?
Основная догма, которую необходимо отбросить: «часть меньше целого»
На
Как сравнивать множества
О
В
С
D
А
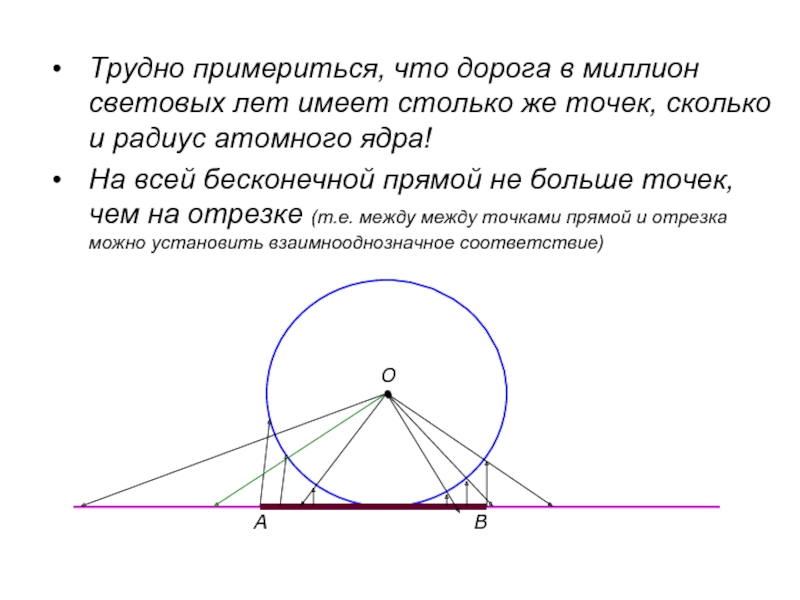
Слайд 22Трудно примериться, что дорога в миллион световых лет имеет столько же
На всей бесконечной прямой не больше точек, чем на отрезке (т.е. между между точками прямой и отрезка можно установить взаимнооднозначное соответствие)
О
А
В
Слайд 23Любой отрезок [a, b] , эквивалентен отрезку [0, 1] .
Доказательство.
Искомое
х у
у =( b - a )x+a.
А также и геометрически:
Слайд 24Тайны бесконечности
Математики и философы всегда интересовались понятием бесконечности.
Парадоксы бесконечности приучили древних
(парадокс Зенона о том, что стрела не может сдвинуться с места, Ахиллес никогда не догонит черепаху)
Например: Евклид, формулировал свою знаменитую теорему о бесконечности простых чисел, выражается так: «Простых чисел существует больше всякого предложенного количества простых чисел», а бесконечно много или нет – об этом Евклид умалчивает.
Основные заслуги в развитии теории множеств принадлежат Г. Кантору (родился в 1845 г в Петербурге, умер в 1918 г в Галле).
Исследования бесконечных множеств потребовало развития математической логики. Первоначально эта область математики была очень далека
от практических приложений, но впоследствии её принципы составили идейную основу конструирования электронных вычислительных машин и программирования вычислений на этих машинах.
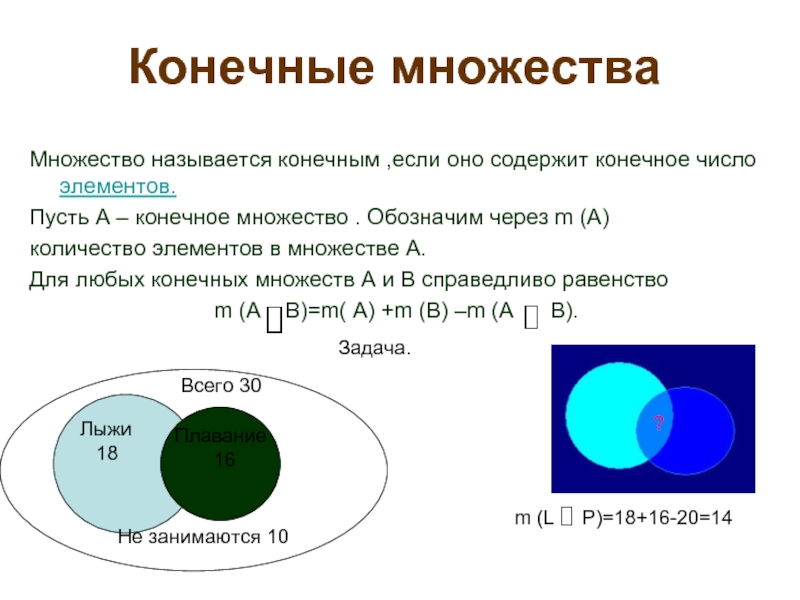
Слайд 25Конечные множества
Множество называется конечным ,если оно содержит конечное число элементов.
Пусть А
количество элементов в множестве А.
Для любых конечных множеств А и В справедливо равенство
m (A B)=m( A) +m (B) –m (A B).
Задача.
Лыжи
18
Плавание
16
Не занимаются 10
Всего 30
?
m (L P)=18+16-20=14
Слайд 26Задачи
Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30
Определите разность множеств А и В, разность множеств В и А ,пересечение множеств и объединение множеств.
А={1,2,3,4,5,6}, В={2,4,6,8,10}.
В классе 32 ученика. 12 учеников занимаются волейболом, 15 – баскетболом, 8 – и баскетболом, и волейболом. Сколько человек не занимаются ни тем, на другим?
В третьем классе дети коллекционируют марки и монеты. Марки коллекционируют 8 человек, монеты – 5 человек. Всего коллекционируют 11 человек. Сколько человек коллекционируют только марки и монеты?
Экзамен по математике сдавали 250 абитуриентов. Оценку ниже 5 баллов получили 180 человек, а выдержали экзамен 210 абитуриентов. Сколько человек получили оценку 3 и 4?
Слайд 27Задание
1. Найдите объединение и пересечение множеств А и В, если
А={a,
2. Каждый ребенок в группе изучает английский или французский язык. Английский язык изучают 25 детей, французский – 27 детей, а тот и другой – 18 человек. Сколько детей в группе?
3. В группе детского сада 25 детей, среди них 20 детей младше 6 лет и 15 детей старше 7 лет. может ли быть такое?
4. В группе 25 студентов, из них 19 человек предпочитают волейбол, а 8 человек – волейбол и баскетбол. Сколько студентов может играть в баскетбол?
5. Из 38 учащихся класса 24 занимаются в хоре и 15 – в лыжной секции. Сколько учащихся занимается и в хоре, и в лыжной секции, если в классе нет учащихся, не посещающих занятий хора или лыжной секции?
6. В школьной олимпиаде по математике участвовали 100 человек, по физике – 50, по информатике – 48. Когда учеников опросили: в скольких участвовали в школьных олимпиадах, ответ «в двух» дали вдвое меньше, чем «в одной», а «в трех» втрое меньше, чем «в одной». Сколько всего учеников участвовало в олимпиадах?

















![Любой отрезок [a, b] , эквивалентен отрезку [0, 1] . Доказательство.Искомое взаимно однозначное соответствие можно](/img/tmb/1/96593/0da66918b234c22061902e93b92ebfbf-800x.jpg)