- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Комплексные числа презентация
Содержание
- 1. Комплексные числа
- 2. ПЛАН: Основные понятия. Формы записи. Действия над
- 3. Основные понятия. Определение. Комплексным числом Ζ
- 4. Основные понятия. Два комплексных числа называются
- 5. Примеры. Пример 1. Пример 2.
- 6. Геометрическое изображение комплексных чисел. Всякое комплексное
- 7. Геометрическое изображение комплексных чисел. Плоскость,
- 8. Геометрическое изображение комплексных чисел. Комплексное число можно
- 9. Формы записи комплексных чисел. Алгебраическая. Тригонометрическая.
- 10. Формы записи комплексных чисел. Запись числa
- 11. Переход от одной формы к другой. От
- 12. При переходе от алгебраической формы комплексного числа
- 13. Пример: Комплексное число изобразить на плоскости и
- 14. Комплексное число можно записать в показательной
- 15. 2. Действия над комплексными числами Суммой двух
- 16. Сложение (вычитание) комплексных чисел Примеры: 1. 2.
- 17. Произведение и частное комплексных чисел в алгебраической
- 18. Произведение и частное комплексных чисел в алгебраической форме. Произведение: Частное:
- 19. Произведение и частное комплексных чисел в тригонометрической
- 20. Произведение и частное комплексных чисел в тригонометрической форме. Произведение: Частное:
- 21. Произведение и частное комплексных чисел в показательной форме.
- 22. Возведение комплексных чисел в степень. Правило умножения
- 23. Возведение комплексных чисел в степень. Пример. Найти
- 24. Извлечение корней из комплексных чисел в тригонометрической
- 25. Извлечение корней из комплексных чисел. Пример.
ПЛАН: Основные понятия. Формы записи. Действия над комплексными числами: Сложение комплексных чисел; Вычитание комплексных чисел; Умножение комплексных чисел; Деление комплексных чисел ; Возведение в n-степень; Извлечение корней из комплексных чисел.
Слайд 2ПЛАН:
Основные понятия. Формы записи.
Действия над комплексными числами:
Сложение комплексных чисел;
Вычитание комплексных чисел;
Умножение
комплексных чисел;
Деление комплексных чисел ;
Возведение в n-степень;
Извлечение корней из комплексных чисел.
Деление комплексных чисел ;
Возведение в n-степень;
Извлечение корней из комплексных чисел.
Слайд 3Основные понятия.
Определение.
Комплексным числом Ζ называется выражение вида
,
где α и β- действительные числа, а i - мнимая единица, и
Например, Ζ1 = 6+2i или Ζ2 = 1-5i .
Число α называется действительной частью комплексного числа и обозначается α=Re z,
а β − мнимой частью и обозначается β=Im z.
где α и β- действительные числа, а i - мнимая единица, и
Например, Ζ1 = 6+2i или Ζ2 = 1-5i .
Число α называется действительной частью комплексного числа и обозначается α=Re z,
а β − мнимой частью и обозначается β=Im z.
Слайд 4Основные понятия.
Два комплексных числа называются равными тогда и только тогда, когда
равны их действительные и мнимые части.
Два комплексных числа, отличающихся лишь знаком мнимой части, называются комплексно- сопряженными.
Два комплексных числа, отличающихся лишь знаком мнимой части, называются комплексно- сопряженными.
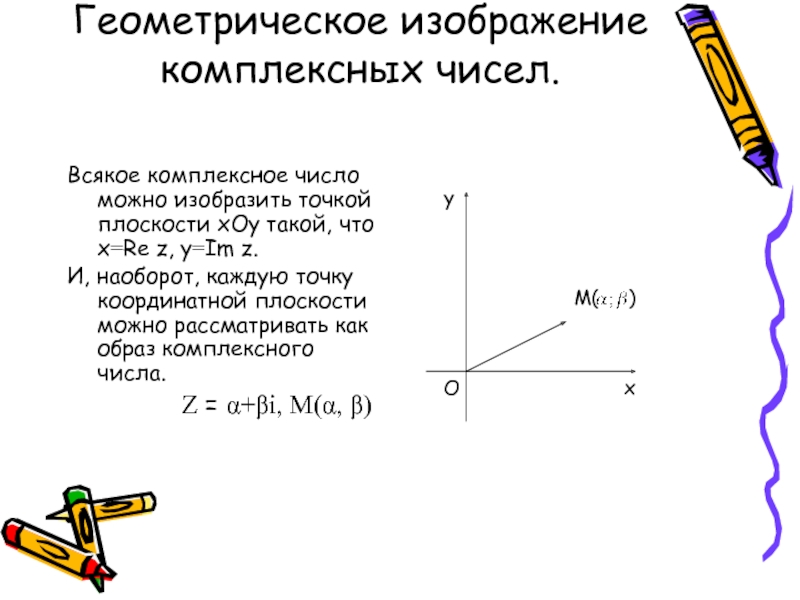
Слайд 6Геометрическое изображение комплексных чисел.
Всякое комплексное число можно изобразить точкой плоскости xOy
такой, что x=Re z, y=Im z.
И, наоборот, каждую точку координатной плоскости можно рассматривать как образ комплексного числа.
Ζ = α+βi, М(α, β)
И, наоборот, каждую точку координатной плоскости можно рассматривать как образ комплексного числа.
Ζ = α+βi, М(α, β)
Слайд 7Геометрическое изображение комплексных чисел.
Плоскость, на которой изображается комплексные числа, называется комплексной
плоскостью.
Ось абсцисс Ox называется действительной осью.
Ось ординат Oy называется мнимой осью.
Ось абсцисс Ox называется действительной осью.
Ось ординат Oy называется мнимой осью.
Слайд 8Геометрическое изображение комплексных чисел.
Комплексное число можно задавать с помощью радиус-вектора
.
Длина вектора называется модулем этого числа и обозначается фΖ фили r .
Величина угла между положительным направлением оси Ox и вектором
называется аргументом этого комплексного числа и обозначается Arg Ζ или ϕ.
Аргумент комплексного числа определяется с точностью до слагаемого 2πκ.
Длина вектора называется модулем этого числа и обозначается фΖ фили r .
Величина угла между положительным направлением оси Ox и вектором
называется аргументом этого комплексного числа и обозначается Arg Ζ или ϕ.
Аргумент комплексного числа определяется с точностью до слагаемого 2πκ.
φ
Слайд 9Формы записи
комплексных чисел.
Алгебраическая.
Тригонометрическая.
Показательная.
Любое комплексное число
можно записать в любой форме.
Слайд 10Формы записи
комплексных чисел.
Запись числa
z=α+βi
называется
алгебраической формой комплексного числа.
Запись числа
z в виде z=r(cosφ+isinφ)
называется тригонометрической формой
комплексного числа.
комплексного числа.
Модуль r и аргумент ϕ можно рассматривать как полярные координаты вектора
Тогда получаем
Комплексное число z=α+βi можно записать в виде
Или
Слайд 11Переход от одной формы к другой.
От алгебраической формы к тригонометрической
Т.к.
То
От тригонометрической формы к алгебраической
Слайд 12При переходе от алгебраической формы комплексного числа к тригонометрической достаточно определить
главное значение аргумента, т.е.
Т.к.
то
Слайд 13Пример: Комплексное число изобразить на плоскости и записать в тригонометрической форме
2
2
φ
x
y
0
Слайд 14Комплексное число можно записать в показательной
(или экспонентной) форме
Где
и
В силу формулы Эйлера
функция периодическая с основным периодом 2π.
Для записи комплексного числа в показательной форме надо определить главное значение аргумента и модуль.
В силу формулы Эйлера
функция периодическая с основным периодом 2π.
Для записи комплексного числа в показательной форме надо определить главное значение аргумента и модуль.
Слайд 152. Действия над комплексными числами
Суммой двух комплексных чисел
Называется комплексное число
Разностью двух комплексных чисел
Называется комплексное число
Геометрически комплексные числа складываются и вычитаются, как векторы.
Слайд 17Произведение и частное комплексных чисел в алгебраической форме.
Произведением двух комплексных чисел
называется
комплексное число
Формула получается путем перемножения двучленов!
Формула получается путем перемножения двучленов!
Частным двух комплексных чисел
называется комплексное число
На практике используют умножение числителя и знаменателя на число, сопряженное знаменателю!
Слайд 19Произведение и частное комплексных чисел в тригонометрической форме.
Произведение чисел
Находим по формуле
При
умножении модули перемножаются, а аргументы складываются!
Частное чисел
Находим по формуле
При делении модули делятся, а аргументы вычитаются!
Слайд 22Возведение комплексных чисел в степень.
Правило умножения комплексных чисел позволяет возвести число
в n-степень:
Получим Формулу Муавра:
Для показательной формы используют формулу:
Получим Формулу Муавра:
Для показательной формы используют формулу:
Слайд 23Возведение комплексных чисел в степень.
Пример.
Найти
Запишем число в тригонометрической форме:
Слайд 24Извлечение корней из комплексных чисел в тригонометрической форме.
Определение.
Корнем n-й
степени из комплексного числа z называется комплексное число ω, удовлетворяющее равенству:
Данное действие выполняется над комплексными числами в тригонометрической форме.
Получим n различных корней!
Данное действие выполняется над комплексными числами в тригонометрической форме.
Получим n различных корней!
Слайд 25Извлечение корней из комплексных чисел.
Пример.
Найти
, если
В тригонометрической форме число имеет вид:
Используем формулу:
Найдем 6 возможных корней, придавая k последовательно значения 0,1,2,3,4,5:
В тригонометрической форме число имеет вид:
Используем формулу:
Найдем 6 возможных корней, придавая k последовательно значения 0,1,2,3,4,5:
