- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория комплексных чисел. Показательная форма комплексного числа. (Тема 4) презентация
Содержание
- 1. Теория комплексных чисел. Показательная форма комплексного числа. (Тема 4)
- 2. Показательная форма комплексного числа Если комплексному числу
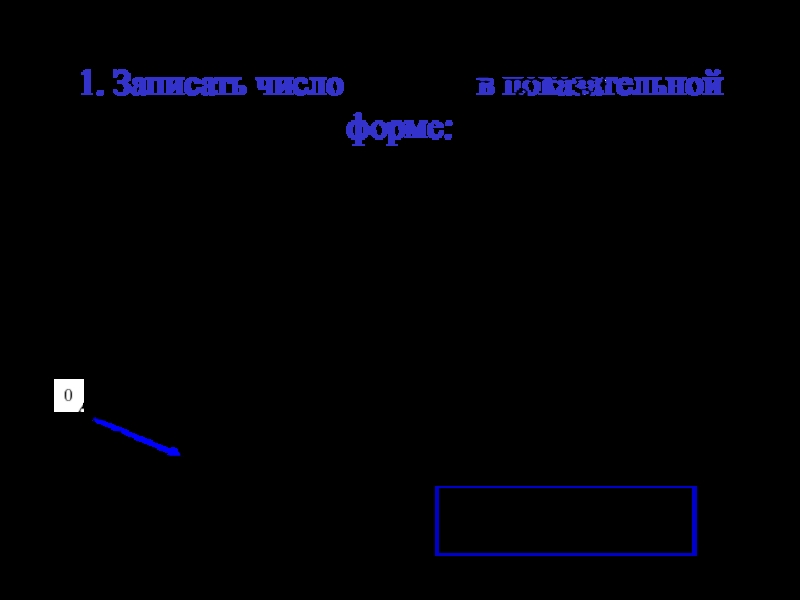
- 3. 1. Записать число в показательной форме:
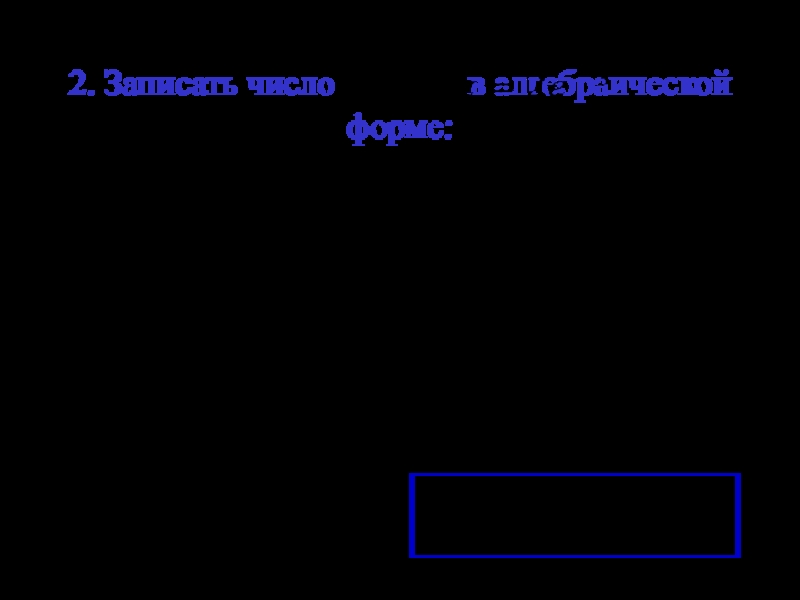
- 4. 2. Записать число в алгебраической форме:
- 5. Действия над комплексными числами в показательной форме Пусть
- 6. Доказательства Пусть
- 7. 3. Найти произведение и частное комплексных чисел:
- 8. 4. Представить в показательной форме комплексное число:
- 9. Пусть Запишем каждое из чисел в показательной форме.
- 10. х у 1 0 ϕ
- 11. х у 1 0 ϕ -1
- 12. или
- 13. 5. Представить в показательной форме комплексное число:
- 14. х у 1 0 ϕ -1 Пусть
- 16. 6. Записать все значения корня в показательной форме.
- 17. х у 1 0 ϕ Запишем данное число в показательной форме: Пусть
- 19. Пусть тогда
- 20. 5. Показать, что
- 21. 6. Показать, что
- 22. 7. Записать число в тригонометрической форме.
Показательная форма комплексного числа Если комплексному числу модуль которого равен 1, поставить в соответствие показательное выражение еiϕ,то получим соотношение которое называется формулой Эйлера
Слайд 2Показательная форма комплексного числа
Если комплексному числу
модуль которого равен 1, поставить
в соответствие показательное
выражение еiϕ,то получим соотношение
которое называется формулой Эйлера
показательная форма
выражение еiϕ,то получим соотношение
которое называется формулой Эйлера
показательная форма
Слайд 19Пусть
тогда
Формулами пользуются, в частности, для выражения степеней
cosφ и sinφ и их произведений через cos и sin кратных дуг.
Слайд 227. Записать число в тригонометрической форме.
комплексная степень числа е
Для степени е
с комплексным показателем сохраняются все свойства степеней с действительными показателями.
