- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Параллельность прямой и плоскости презентация
Содержание
- 1. Параллельность прямой и плоскости
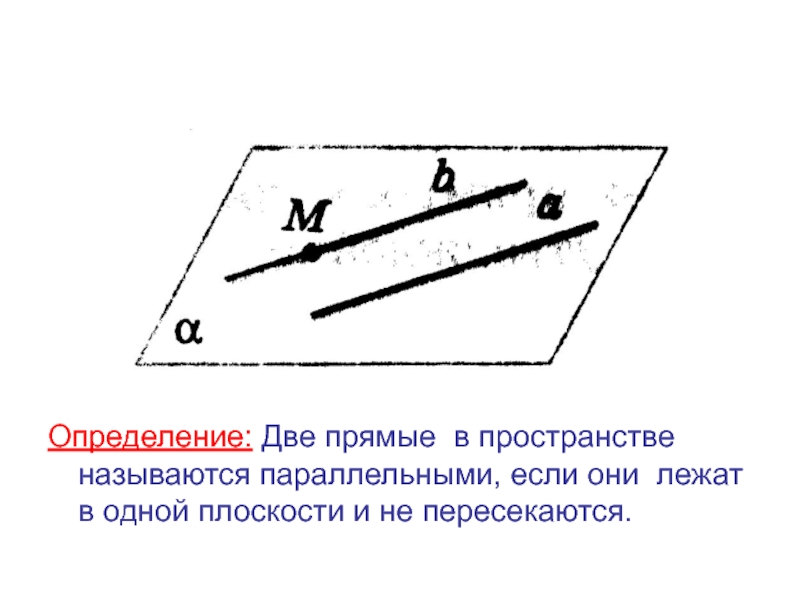
- 2. Определение: Две прямые в пространстве называются параллельными,
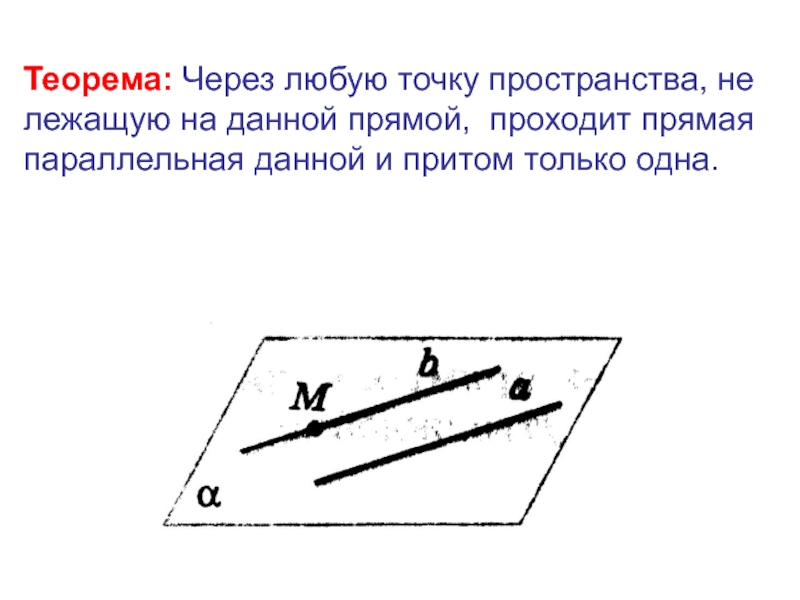
- 3. Теорема: Через любую точку пространства, не лежащую
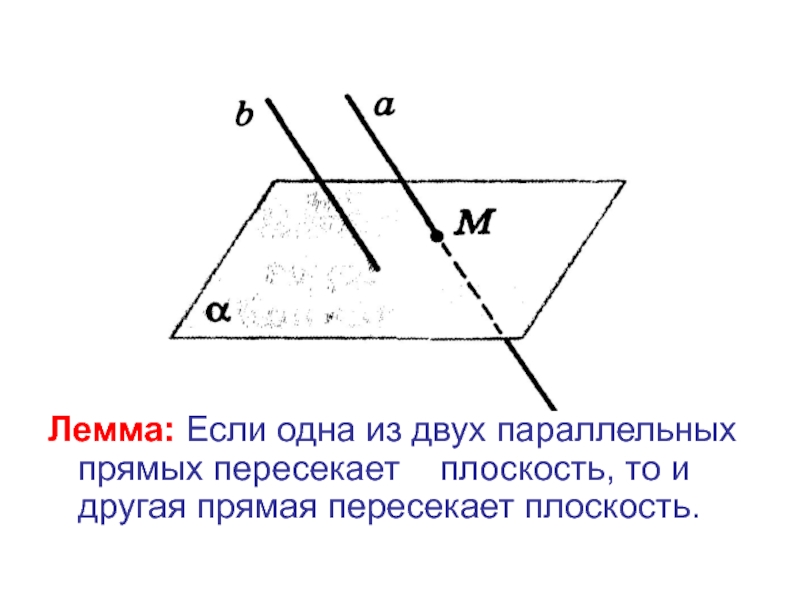
- 4. Лемма: Если одна из двух параллельных прямых
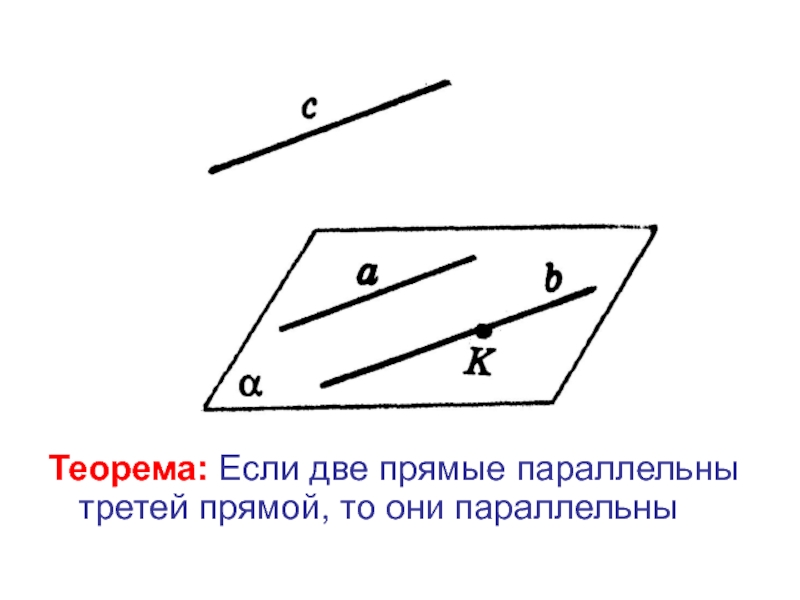
- 5. Теорема: Если две прямые параллельны третей прямой, то они параллельны
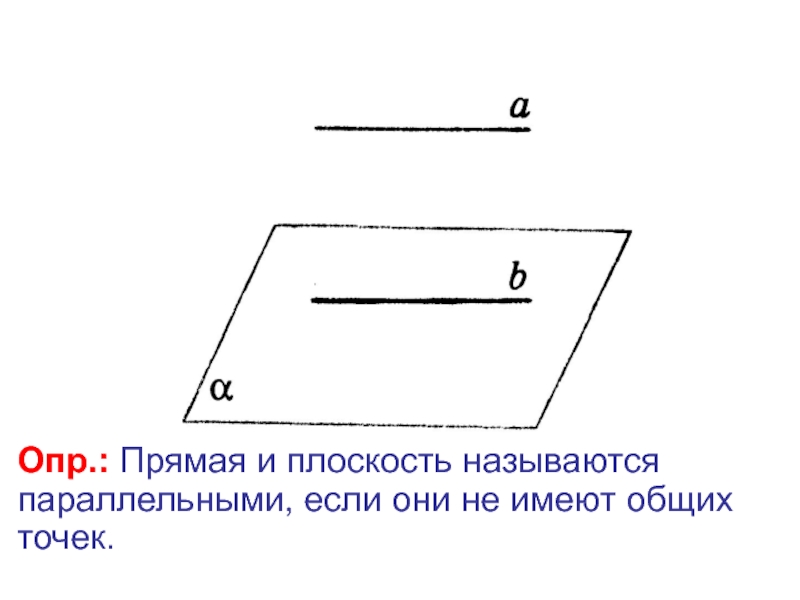
- 6. Опр.: Прямая и плоскость называются параллельными, если они не имеют общих точек.
- 7. Теорема (признак параллельности прямой и плоскости): Если
- 8. Свойства прямой и плоскости. Теорема 1: Если
- 9. Теорема 2: Если одна из двух параллельных
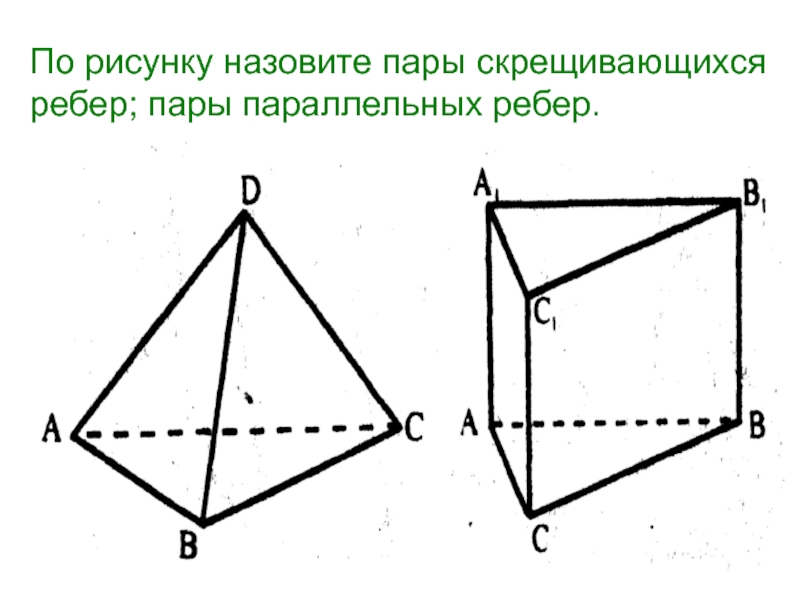
- 10. По рисунку назовите пары скрещивающихся ребер; пары параллельных ребер.
- 11. На модели куба укажите: а)
- 12. АВСDА1В1С1D1 - куб. Все грани -
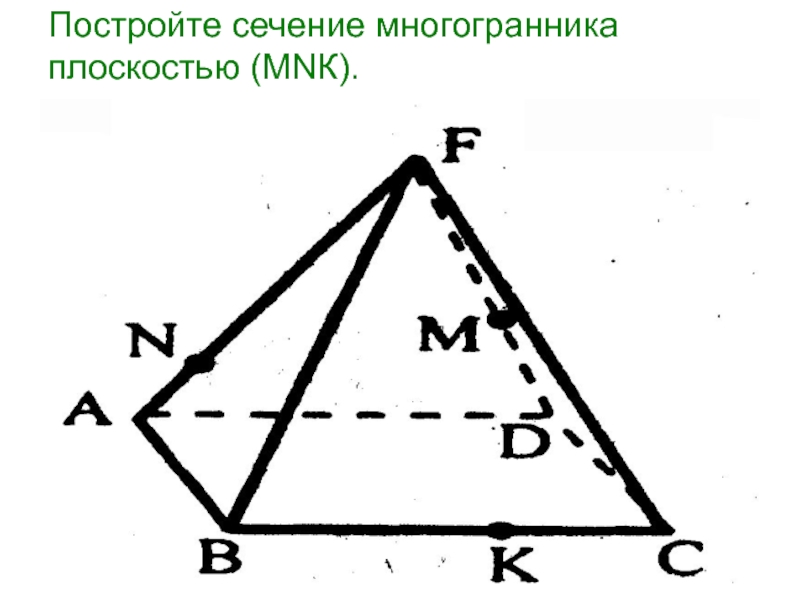
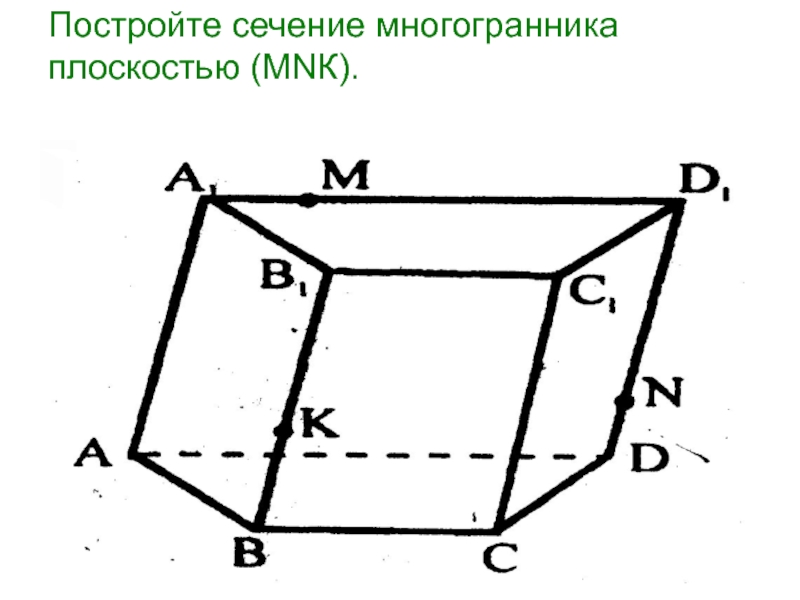
- 13. Постройте сечение многогранника плоскостью (МNК).
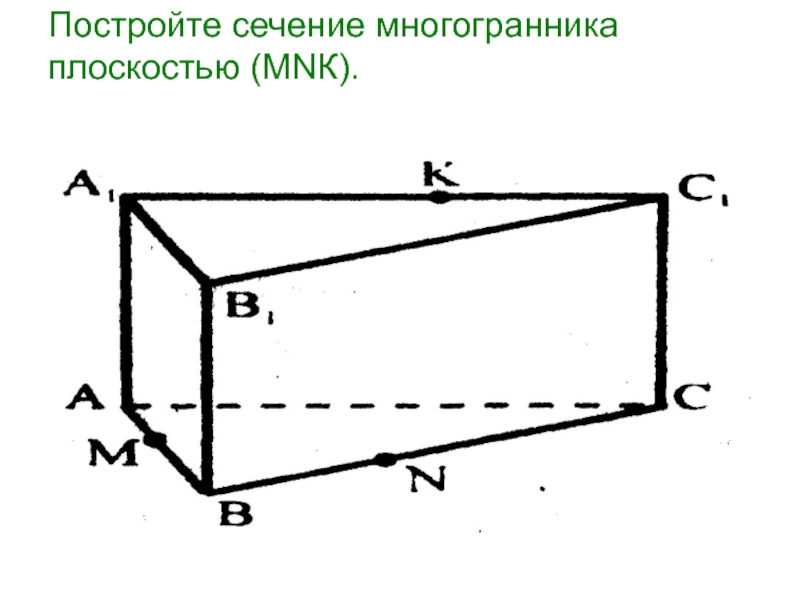
- 14. Постройте сечение многогранника плоскостью (МNК).
- 15. Постройте сечение многогранника плоскостью (МNК).
- 16. Домашнее задание: Стр. 9-13, № 27, 28,31,54
Слайд 2Определение: Две прямые в пространстве называются параллельными, если они лежат в
одной плоскости и не пересекаются.
Слайд 3Теорема: Через любую точку пространства, не лежащую на данной прямой, проходит
прямая параллельная данной и притом только одна.
Слайд 4Лемма: Если одна из двух параллельных прямых пересекает плоскость, то
и другая прямая пересекает плоскость.
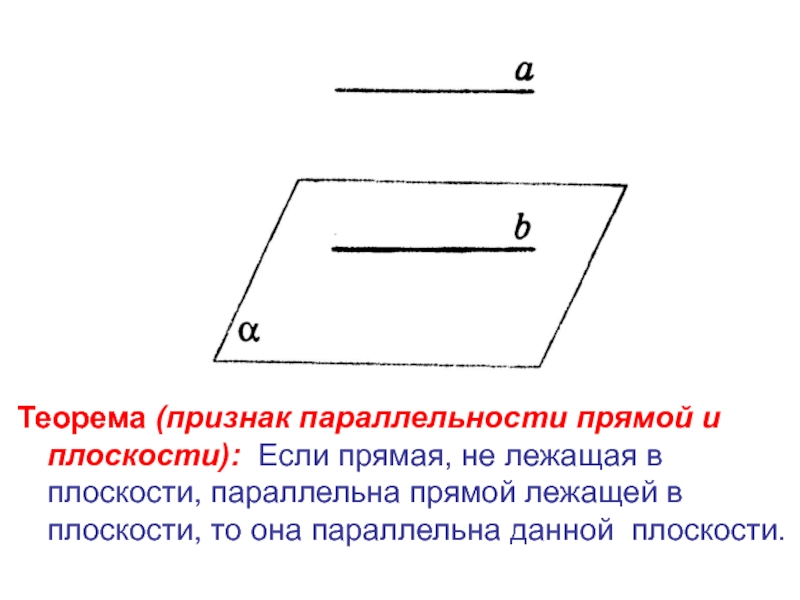
Слайд 7Теорема (признак параллельности прямой и плоскости): Если прямая, не лежащая в
плоскости, параллельна прямой лежащей в плоскости, то она параллельна данной плоскости.
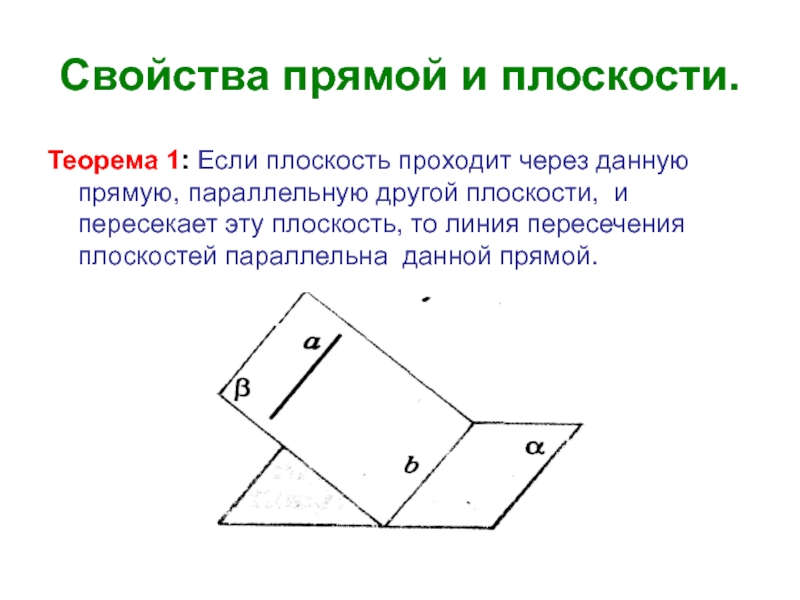
Слайд 8Свойства прямой и плоскости.
Теорема 1: Если плоскость проходит через данную прямую,
параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
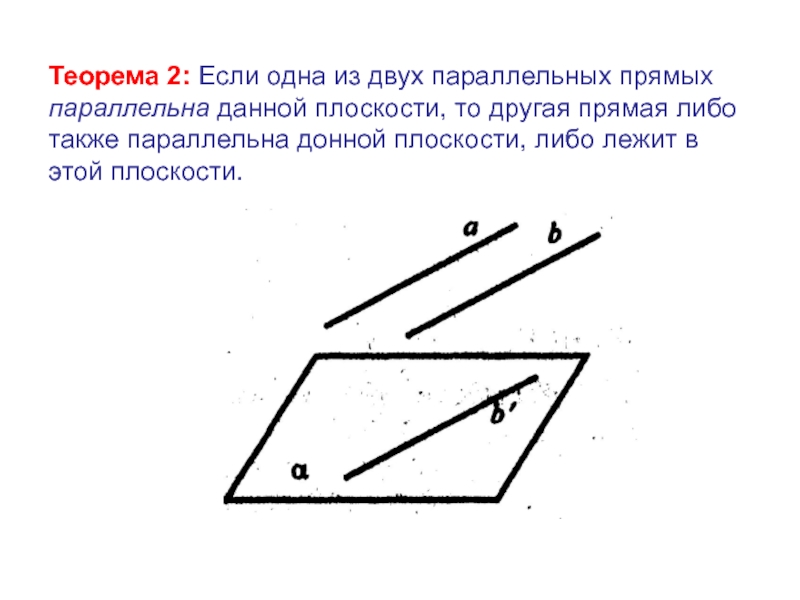
Слайд 9Теорема 2: Если одна из двух параллельных прямых параллельна данной плоскости,
то другая прямая либо также параллельна донной плоскости, либо лежит в этой плоскости.
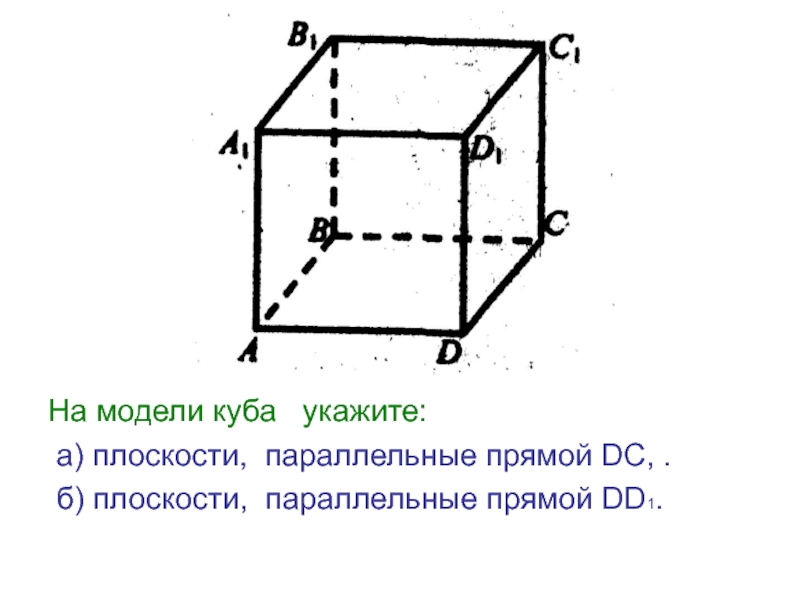
Слайд 11На модели куба укажите:
а) плоскости, параллельные прямой DC, .
б) плоскости, параллельные прямой DD1.
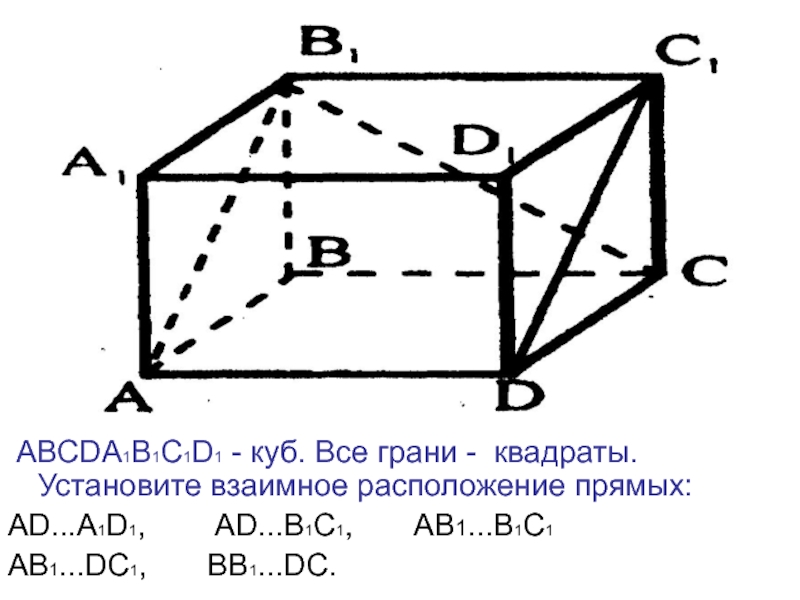
Слайд 12 АВСDА1В1С1D1 - куб. Все грани - квадраты. Установите взаимное расположение
прямых:
АD...А1D1, АD...В1С1, АВ1...В1С1
АВ1...DC1, BB1...DC.
АD...А1D1, АD...В1С1, АВ1...В1С1
АВ1...DC1, BB1...DC.