- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема о площади треугольника презентация
Содержание
- 1. Теорема о площади треугольника
- 2. Цели: - доказать теорему о площади треугольника;
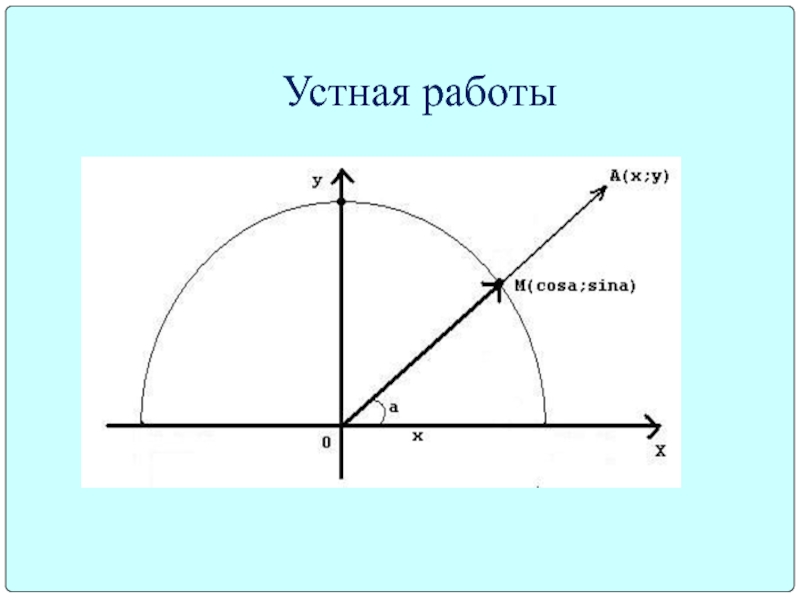
- 4. Устная работы
- 5. Формулы площади треугольника S= ab,
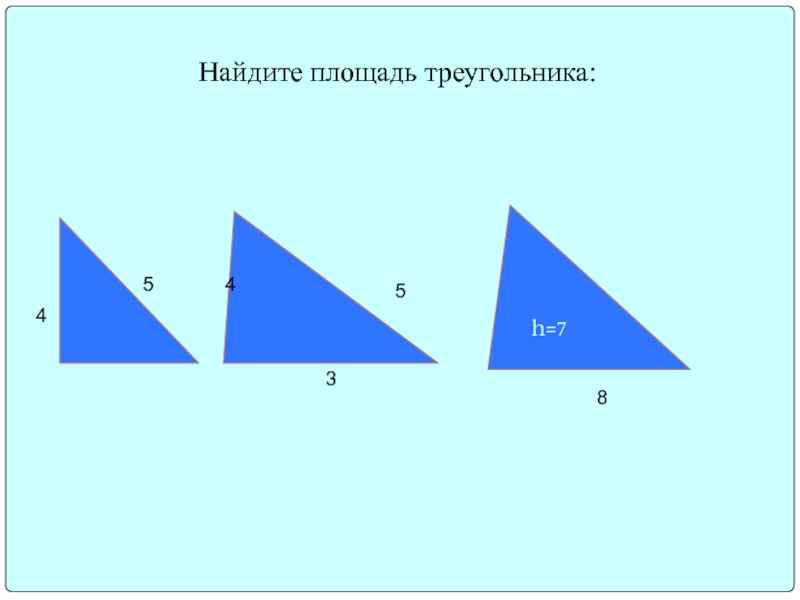
- 6. Найдите площадь треугольника: h=7 4 5 4 5 8 3
- 7. Ответы: 6; 6; 28
- 8. Теорема о площади треугольника Дано: ABC, BC=a,
- 9. Решение задач 1) № 1020(а) Дано: АВС,
- 10. Самостоятельная работа по вариантам ( 3 уровня)
- 11. Домашнее задание П. 96 (доказательство теоремы) № 1020 (б, в ) , 1021, 1023
Цели: - доказать теорему о площади треугольника; - научить учащихся решать задачи на применение теоремы о площади треугольника; -активизировать познавательную деятельность учащихся, поддержать интерес к предмету; - воспитывать уважение друг к
Слайд 2Цели:
- доказать теорему о площади треугольника;
- научить учащихся решать задачи на
применение теоремы о площади треугольника;
-активизировать познавательную деятельность учащихся, поддержать интерес к предмету;
- воспитывать уважение друг к другу, взаимопонимание, уверенность в себе.
-активизировать познавательную деятельность учащихся, поддержать интерес к предмету;
- воспитывать уважение друг к другу, взаимопонимание, уверенность в себе.
Слайд 3
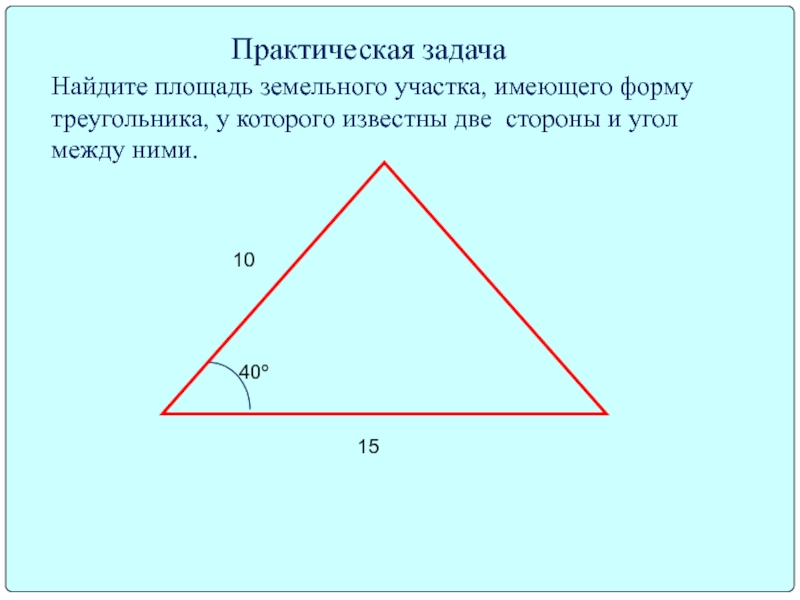
10
15
40º
Практическая задача
Найдите площадь земельного участка, имеющего форму треугольника, у которого известны две стороны и угол между ними.
Слайд 5Формулы площади треугольника
S= ab, где а, в - катеты
прямоугольного треугольника
S= ah, где а - основание треугольника, h- высота
S=
S= ah, где а - основание треугольника, h- высота
S=
р- полупериметр, а, в, с- стороны треугольника
Слайд 8Теорема о площади треугольника
Дано:
ABC, BC=a, CA=b,
S -площадь треугольника.
Доказать: S=
absinC
Доказательство: S= ah, h=bsinC.
Сл. S= absinC
Доказательство: S= ah, h=bsinC.
Сл. S= absinC
А(bcos C; bsin C)
h
c
B
C
b
a
Теорема: Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
Слайд 9Решение задач
1) № 1020(а)
Дано: АВС, АВ = 6 см,
АС = 4 см, <А = 60˚
Найти: S = ?
Ответ: 12
2) № 1022
Дано: S = 60 см, АС = 15 см, <А = 30˚
Найти: АВ = ?
Ответ: 16 см.
3) Найти площадь равнобедренного треугольника с углом при основании 15˚ и боковой стороной, равной 5 см.
Ответ: см .
4) В параллелограмме АВСD АВ = 6, АD = 4, sinA = 0,8. Найдите большую высоту параллелограмма.
Ответ: 4,8
5) . Основания равнобедренной трапеции равны 6 и 12. Синус острого угла трапеции равен 0,8. Найдите боковую сторону трапеции
Ответ: 5
Найти: S = ?
Ответ: 12
2) № 1022
Дано: S = 60 см, АС = 15 см, <А = 30˚
Найти: АВ = ?
Ответ: 16 см.
3) Найти площадь равнобедренного треугольника с углом при основании 15˚ и боковой стороной, равной 5 см.
Ответ: см .
4) В параллелограмме АВСD АВ = 6, АD = 4, sinA = 0,8. Найдите большую высоту параллелограмма.
Ответ: 4,8
5) . Основания равнобедренной трапеции равны 6 и 12. Синус острого угла трапеции равен 0,8. Найдите боковую сторону трапеции
Ответ: 5
