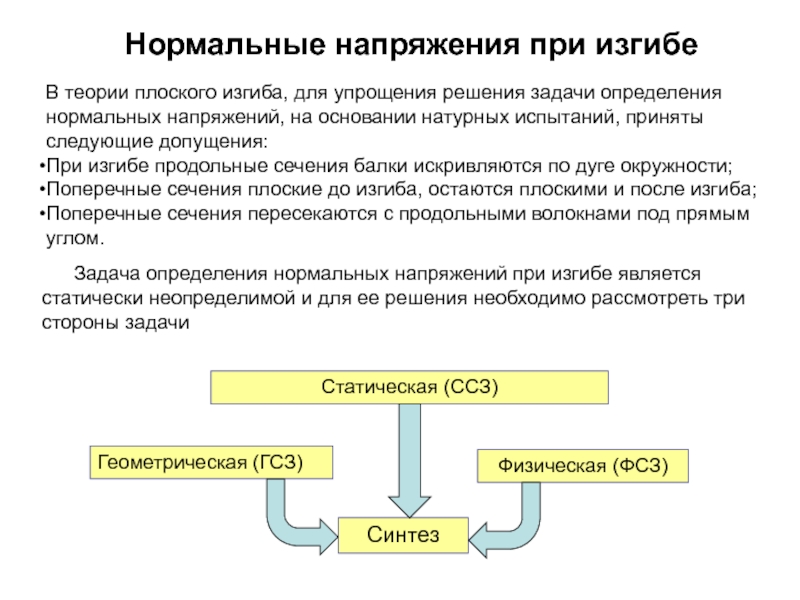
интервал сходимости этого ряда (-R,R). Тогда говорят, что функция f(x) разлагается в степенной ряд на интервале (-R,R).
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Свойства степенных рядов презентация
Содержание
Слайд 2
1
На любом отрезке [a,b], целиком
принадлежащем интервалу сходимости (-R,R)
функция f(x)
является непрерывной,
и, следовательно, степенной ряд можно
почленно интегрировать на этом отрезке:
и, следовательно, степенной ряд можно
почленно интегрировать на этом отрезке:
Слайд 4
Ряды, полученные в результате дифференцирования или интегрирования, имеют тот же радиус
сходимости R.

![1На любом отрезке [a,b], целиком принадлежащем интервалу сходимости (-R,R) функция f(x) является непрерывной, и, следовательно,](/img/tmb/6/502132/f541cd84e93d63bb806e480701a816ea-800x.jpg)