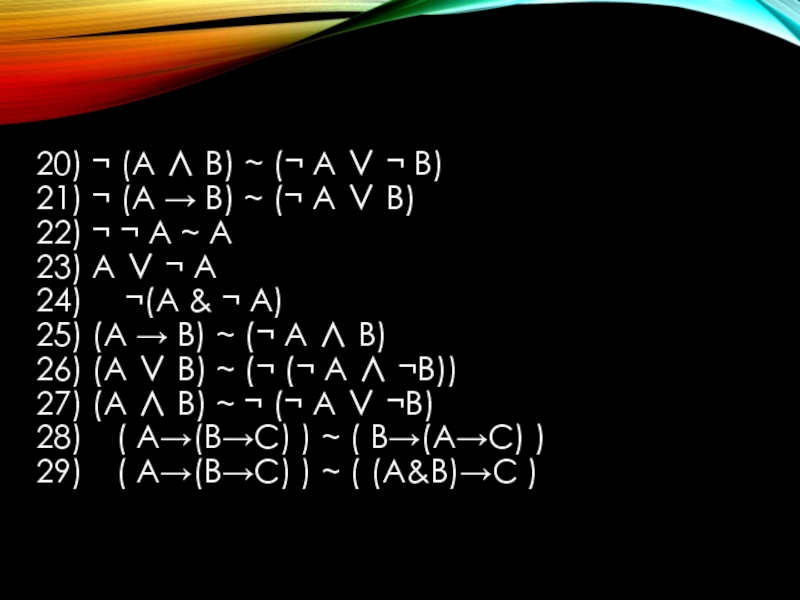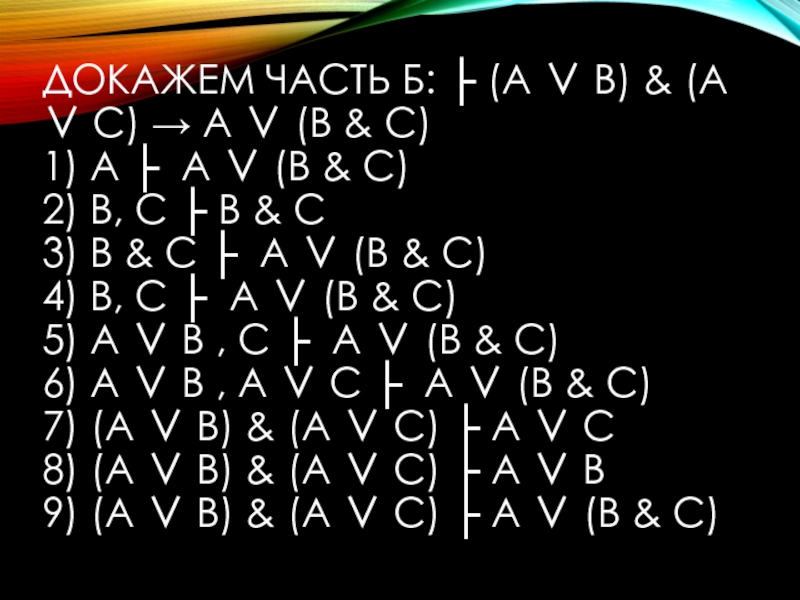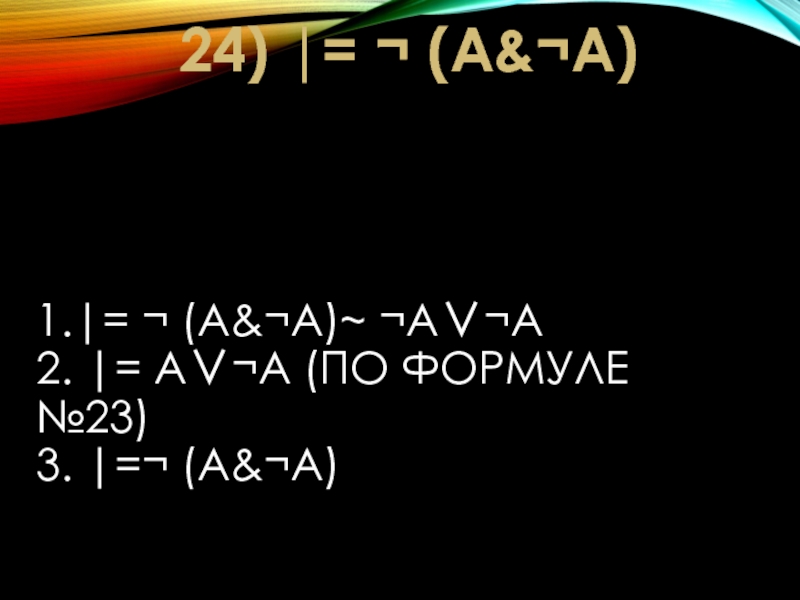- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математическая логика презентация
Содержание
- 2. ОСНОВНЫЕ ТАВТОЛОГИИ 1. |=A→(B→A) 2. |=(A→B)→((A→(B→C))→(A→C)) 3.
- 3. ПРАВИЛО ВЫВОДА (MODUS PONENS):
- 4. ОПР. ФОРМУЛА A НАЗЫВАЕТСЯ ВЫВОДИМОЙ В
- 5. ОПР. ФОРМУЛА
- 6. ПРАВИЛА ВВЕДЕНИЯ И УДАЛЕНИЯ
- 7. ЕСЛИ Γ ∪ {A}
- 8. 9)A→A 10)(А → В) → ((В →
- 9. 20) ¬ (А ∧ В) ~ (¬
- 10. 1. A→(A→A) СХ. 1; 2. (A→(A→A))→((A→((A→ A)→
- 11. ЕСЛИ ДОКАЖЕМ ЧТО СУЩЕСТВУЮТ : А
- 12. ТРЕБУЕТСЯ ДОКАЗАТЬ А ├ (¬ А →
- 13. ├ А & (В & С)
- 14. 1) А, А → В, ¬ В
- 15. 1 ЧАСТЬ : ┣ A&(B&C) →
- 16. А) ├ А ∨ (В ∨ С)
- 17. ├ ((А & В) → (В
- 18. ├ (А ∨ В → В ∨
- 19. A) A & (В ∨ С)
- 20. ДОКАЖЕМ ЧАСТЬ Б ПО СЛЕДУЮЩЕЙ СХЕМЕ: (А
- 21. А) ├ A ∨ (В & С)
- 22. ДОКАЖЕМ ЧАСТЬ Б: ├ (А ∨ В)
- 23. А) ├ ¬ (А ∨
- 24. А) ├ ¬ (А & В)
- 25. I. |=¬¬A ~ A II. |=A
- 26. 1. ¬A, ¬ (A∨¬A) |=¬A∨A (ВВЕДЕНИЕ ∨)
- 27. 1.|= ¬ (A&¬A)~ ¬A∨¬A 2.
- 28. I. A → B|=¬A∨B II.
Слайд 2ОСНОВНЫЕ ТАВТОЛОГИИ
1. |=A→(B→A)
2. |=(A→B)→((A→(B→C))→(A→C))
3. |=A→(B→A&B)
4А. |=A&B→A
4Б. |=A&B→B
5А. |=A→A∨B
5Б. |=B→A∨B
6. |=(A→C)→((B→C))→(A∨B→C))
7.|=(A→B)→(A→¬B)→¬A
8. ¬¬А→A
Слайд 3 ПРАВИЛО ВЫВОДА (MODUS PONENS):
(MP).
ОПР.
ВЫВОДОМ НАЗЫВАЕТСЯ КОНЕЧНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ ФОРМУЛ, КАЖДАЯ ИЗ КОТОРЫХ ЯВЛЯЕТСЯ АКСИОМОЙ ИЛИ ПОЛУЧАЕТСЯ ИЗ НЕКОТОРЫХ ПРЕДЫДУЩИХ ФОРМУЛ ПО ПРАВИЛУ ВЫВОДА.
Слайд 4ОПР.
ФОРМУЛА A НАЗЫВАЕТСЯ ВЫВОДИМОЙ В ИСЧИСЛЕНИИ ВЫСКАЗЫВАНИЙ ИЛИ ТЕОРЕМОЙ ИСЧИСЛЕНИЯ
ПРИМЕР: |= A → A.
ДОКАЗАТЕЛЬСТВО.
1) В АКСИОМЕ 2 ВОЗЬМЁМ B = (A → A) И C = A
2) (A → ((A → A) → A)) → ((A → (A → A)) → (A → A))
3) A → (A → A) (1 АКСИОМА)
4) (A → (A → A)) → (A → A) (2,3 MP)
5)A → (A → A) (1 АКСИОМА)
6) A → A (4,5 MP )
Слайд 5ОПР. ФОРМУЛА A НАЗЫВАЕТСЯ ВЫВОДИМОЙ ИЗ МНОЖЕСТВА
ВЫВОДИМОСТЬ ИЗ ГИПОТЕЗ
ОПР.
ПУСТЬ Γ — НЕКОТОРОЕ МНОЖЕСТВО ФОРМУЛ, НАЗЫВАЕМЫХ ГИПОТЕЗАМИ. ВЫВОДОМ ИЗ Γ НАЗЫВАЕТСЯ КОНЕЧНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ ФОРМУЛ, КАЖДАЯ ИЗ КОТОРЫХ ЛИБО ПРИНАДЛЕЖИТ МНОЖЕСТВУ Γ, ЛИБО ЯВЛЯЕТСЯ АКСИОМОЙ, ЛИБО ПОЛУЧАЕТСЯ ИЗ ПРЕДЫДУЩИХ ФОРМУЛ ПО ПРАВИЛУ ВЫВОДА.
Слайд 7 ЕСЛИ Γ ∪ {A} ├ B, ТО Γ
ТЕОРЕМА О ДЕДУКЦИИ ДЛЯ ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИЙ
Слайд 89)A→A 10)(А → В) → ((В → С)(А → С)) 11)( А →
ИСПОЛЬЗУЯ ПРИВЕДЕННЫЕ ВЫШЕ АКСИОМЫ И ТЕОРЕМЫ ПРИВЕДЕМ ДОКАЗАТЕЛЬСТВА СЛЕДУЮЩИХ ВЫСКАЗЫВАНИЙ:
Слайд 920) ¬ (А ∧ В) ~ (¬ А ∨ ¬ В) 21)
Слайд 101. A→(A→A) СХ. 1; 2. (A→(A→A))→((A→((A→ A)→ A))→(A→A), ГДЕ B=A→A, C=A, СХ.
ЗАКОН ТОЖДЕСТВА
9)|=А→А
Слайд 11ЕСЛИ ДОКАЖЕМ ЧТО СУЩЕСТВУЮТ : А → В, В → С, А
10) (А → В) → ((В → С)(А → С))
Слайд 12ТРЕБУЕТСЯ ДОКАЗАТЬ А ├ (¬ А → В) 1) А, ¬ А
11) А → (¬ А → В)
Слайд 13 ├ А & (В & С) ~ (А & В) &
А ~ В: (А → В) & (В → А)
Слайд 141) А, А → В, ¬ В ├ В (УДАЛЕНИЕ →
12) (А → В) → (¬ А → ¬ В)
Слайд 15 1 ЧАСТЬ : ┣ A&(B&C) → (A&B)&C 2 ЧАСТЬ : ┣ (A&B)&C
13) A&(B&C) ~ (A&B)&C
Слайд 16А) ├ А ∨ (В ∨ С) → (А ∨ В)
14)А ∨ (В ∨ С) ~ (А ∨ В) ∨ С
Слайд 17 ├ ((А & В) → (В & А) & ├ (В
15)(А & В) ~ (В & А)
Слайд 18├ (А ∨ В → В ∨ А) & (В ∨
16)(А ∨ В) ~ (В ∨ А)
Слайд 19 A) A & (В ∨ С) ├ (А & В) ∨
17) A & (В ∨ С) ~ (А & В) ∨ (А & С)
Слайд 20ДОКАЖЕМ ЧАСТЬ Б ПО СЛЕДУЮЩЕЙ СХЕМЕ: (А & В) ∨ (А &
Слайд 21А) ├ A ∨ (В & С) → (А ∨ В)
18) A ∨ (В & С) ~ (А ∨ В) & (А ∨ С)
Слайд 22ДОКАЖЕМ ЧАСТЬ Б: ├ (А ∨ В) & (А ∨ С)
Слайд 23 А) ├ ¬ (А ∨ В) → (¬ А & ¬
19) ¬ (А ∨ В) ~ (¬ А & ¬ В)
Слайд 24 А) ├ ¬ (А & В) → (¬ А ∨ ¬
20) ¬ (А & В) ~ (¬ А ∨ ¬ В)
Слайд 25I. |=¬¬A ~ A II. |=A ~ ¬¬ A ЧАСТЬ I
22) |= ¬¬A~ A
Слайд 261. ¬A, ¬ (A∨¬A) |=¬A∨A (ВВЕДЕНИЕ ∨) 2. ¬A, ¬ (A∨¬A)
23) A∨¬A
Слайд 28 I. A → B|=¬A∨B II. ¬A∨B |= A → B ЧАСТЬ
25) |=(A → B) ~ ¬A∨B