плохо в десять раз более.
Аристотель
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Свойства логарифмов презентация
Содержание
- 1. Свойства логарифмов
- 2. Логаифм Пифагор Музыка logab lga lna .
- 3. Логарифм Пифагор Музыка logab lga lna .
- 4. Логарифм Пифагор Музыка Математика - это искусство
- 5. Логарифмы Свойства логарифмов
- 6. Логарифмом числа b по основанию а называется
- 7. Логарифмом числа b по основанию а называется
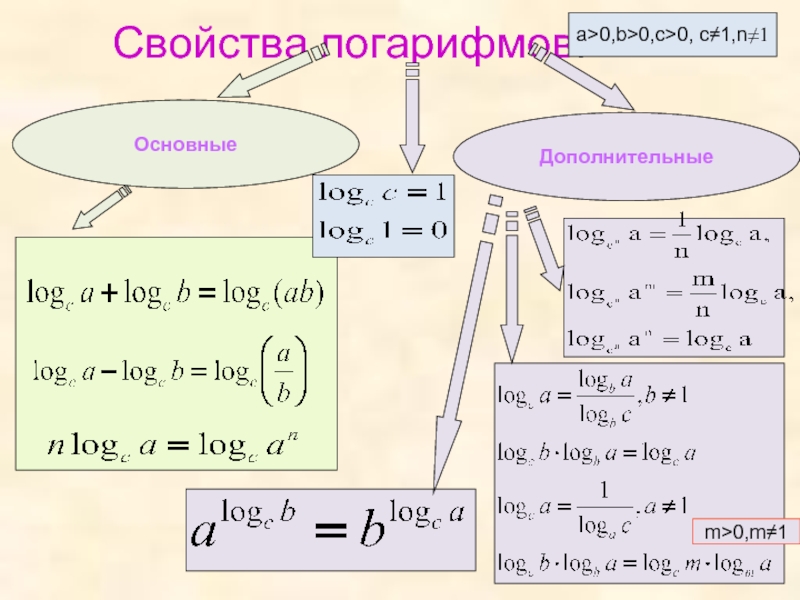
- 8. Свойства логарифмов. a>0,b>0,c>0, c≠1,n≠1 Дополнительные
- 9. Свойства логарифмов a>0,b>0,c>0, c≠1 logaa loga1 logca
- 10. Свойства логарифмов a>0,b>0,c>0, c≠1 logaa loga1 logca
- 13. 1) log 5 25 = 5, так
- 14. Свойства логарифмов n≠1
- 15. Вычислите:
- 16. Софизм рассуждение, кажущееся правильным, но содержащее скрытую
- 17. Логарифмический софизм 2>3 Начнем с неравенства
Логаифм Пифагор Музыка logab lga lna
.
Слайд 4Логарифм
Пифагор
Музыка
Математика - это искусство называть разные вещи одним и тем же
именем.
АНРИ ПУАНКАРЕ
logab
lga
lna
Алгебра – сестра гармонии,
а композиторы – первые программисты
Архитектура, - это застывшая музыка, а
музыка - это ожившая математика
.
Слайд 6Логарифмом числа b по основанию а называется показатель степени, в которую
нужно возвести основание а, чтобы получить число b.
Собери определение
Логарифмом
числа
b
по основанию
а
называется
показатель
степени
,
в которую
нужно
возвести
основание
а,
чтобы
получить
число
b.
Слайд 7Логарифмом числа b по основанию а называется показатель степени, в которую
нужно возвести основание а, чтобы получить число b.
Собери определение
Логарифмом
числа
b
по основанию
а
называется
показатель
степени
,
в которую
нужно
возвести
основание
а,
чтобы
получить
число
b.
Слайд 9Свойства логарифмов
a>0,b>0,c>0, c≠1
logaa
loga1
logca + logcb
logca - logcb
logc(ab)
logc(a/b)
alogab
logabn
nlogab
0
1
b
Слайд 10Свойства логарифмов
a>0,b>0,c>0, c≠1
logaa
loga1
logca + logcb
logca - logcb
logc(ab)
logc(a/b)
alogab
logabn
nlogab
0
1
b
Слайд 131) log 5 25 = 5, так как 5∙5 = 25
Найди
ошибки
2) log 4 (1/16) = 2, так как 4 2 = 1/16
3) log 81 9 = 9, так как 81 = 9∙9
4) 0,3 2log 0,3 6 = 0,3 log 0,3 6∙2 = 0,3 log 0,3 12 = 12
5) log 10 5 + log 10 2 = log 10 (5 + 2) = log 10 7
6) log 1/3 54 – log 1/3 2 = log 1/3 (54-2) = log 1/3 52
Слайд 16Софизм
рассуждение, кажущееся правильным, но содержащее скрытую логическую ошибку и служащее для
придания видимости истинности ложному утверждению.
Обычно софизм обосновывает какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, противоречащее общепринятым представлениям.
Обычно софизм обосновывает какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, противоречащее общепринятым представлениям.
