- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Аппроксимация функций презентация
Содержание
- 1. Аппроксимация функций
- 2. 4.2. Интерполяция многочленами
- 3. Если приближение строится на заданном дискретном множестве
- 4. Теорема. Какие бы ни были
- 6. 4.3. Погрешность интерполирования Погрешность аппроксимации функции
- 7. 4.4. Интерполяционный многочлен Лагранжа
- 14. Погрешность формулы Лагранжа
- 15. Многочлен Лагранжа для равноудаленных узлов
- 18. 4.5. Интерполяционные многочлены Ньютона Конечной разностью
- 19. Таблица конечных разностей
- 20. Первый интерполяционный многочлен Ньютона для равноотстоящих узлов
- 21. Первая интерполяционная формула Ньютона. Используется для интерполирования вперед и экстраполирования назад.
- 22. Второй интерполяционный многочлен Ньютона для равноотстоящих узлов
- 23. Вторая интерполяционная формула Ньютона. Используется для интерполирования назад и экстраполирования вперед.
- 25.
- 26.
- 28. Интерполяционные многочлены Ньютона для неравноотстоящих узлов
- 29. Разделенными разностями порядка k называются отношения:
- 30. Первый интерполяционный многочлен Ньютона с разделенными разностями
- 31. Второй интерполяционный многочлен Ньютона с разделенными разностями
- 32. 4.6. Интерполирование сплайнами Пусть на [a;
- 33. Функция
- 34. Пусть на [a; b] задана сетка
- 35. Узлы сетки - узлы
- 36. Пример
- 43. Интерполяционным кубическим сплайном, соответствующим данной функции f(x), называется функция s(x), удовлетворяющая условиям:
- 47. 4.7. Метод наименьших квадратов
- 48. y = F(x, a, b, c) F(xi,
- 49. yi – F(xi, a, b, c) = εi (i = 1, 2,..., n)
- 50. F(x) = ax + b (*)
- 52. ln F(x) = ln a + mln x в
- 53. ln F(x) = ln a + mx
- 54. В таблице все значения yi
- 55. Все значения xi заменяются на обратные,
- 56. Все значения xi и yi
- 57. Логарифмируем только значения xi. Параметры a и b находятся из системы (*)
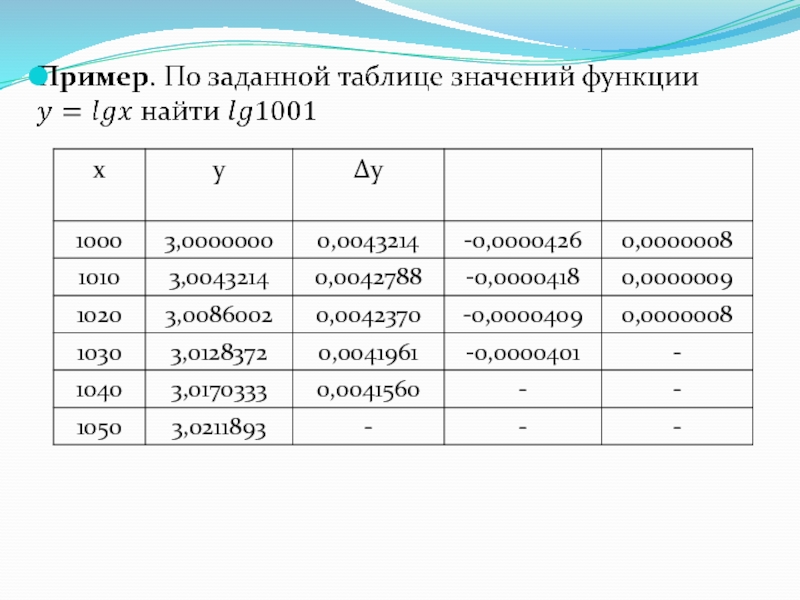
- 58. Пример. По заданной таблице значений x и
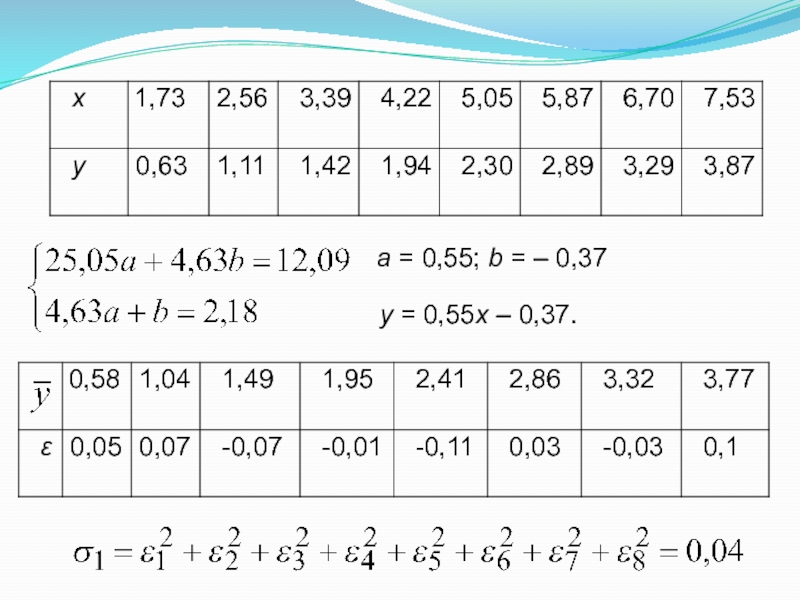
- 59. a = 0,55; b = –
Слайд 1
§ 4 Аппроксимация функций
4.1. Общая задача аппроксимации
Аппроксимацией функции называется приближённое
представление сложной или заданной в виде таблицы функции более простой функцией, имеющей минимальные отклонения от исходной функции.
Слайд 3Если приближение строится на заданном дискретном множестве точек {xi}, то аппроксимация
называется точечной.
При построении приближения на непрерывном множестве точек (например, на отрезке [a, b]) аппроксимация называется непрерывной (или интегральной).
Интерполяция на всем участке [a, b] называется глобальной, а на отдельных участках отрезка [a, b] – кусочной или локальной.
При построении приближения на непрерывном множестве точек (например, на отрезке [a, b]) аппроксимация называется непрерывной (или интегральной).
Интерполяция на всем участке [a, b] называется глобальной, а на отдельных участках отрезка [a, b] – кусочной или локальной.
Слайд 4
Теорема. Какие бы ни были заданы значения функции в n+1 узлах,
всегда существует и притом единственный многочлен степени не выше n, принимающий в этих узлах заданные значения
Слайд 64.3. Погрешность интерполирования
Погрешность аппроксимации функции f (x) полиномом ϕ(x ) можно
оценивать по величине среднеквадратичного отклонения Sa
или по значению максимального отклонения
Слайд 184.5. Интерполяционные многочлены Ньютона
Конечной разностью первого порядка называется разность между двумя
соседними значениями функции f:
Конечной разностью порядка р называется разность двух последовательных разностей порядка р-1:
Конечной разностью порядка р называется разность двух последовательных разностей порядка р-1:
Слайд 20Первый интерполяционный многочлен Ньютона для равноотстоящих узлов
Используется тогда, когда точка, в
которой требуется вычислить приближенное значение функции находится вблизи точки х0
Слайд 21Первая интерполяционная формула Ньютона.
Используется для интерполирования вперед и экстраполирования назад.
Слайд 22Второй интерполяционный многочлен Ньютона для равноотстоящих узлов
Используется тогда, когда точка, в
которой требуется вычислить приближенное значение функции находится вблизи точки хп
Слайд 23Вторая интерполяционная формула Ньютона.
Используется для интерполирования назад и экстраполирования вперед.
Слайд 28Интерполяционные многочлены Ньютона для неравноотстоящих узлов
Разделенными разностями первого порядка называются отношения:
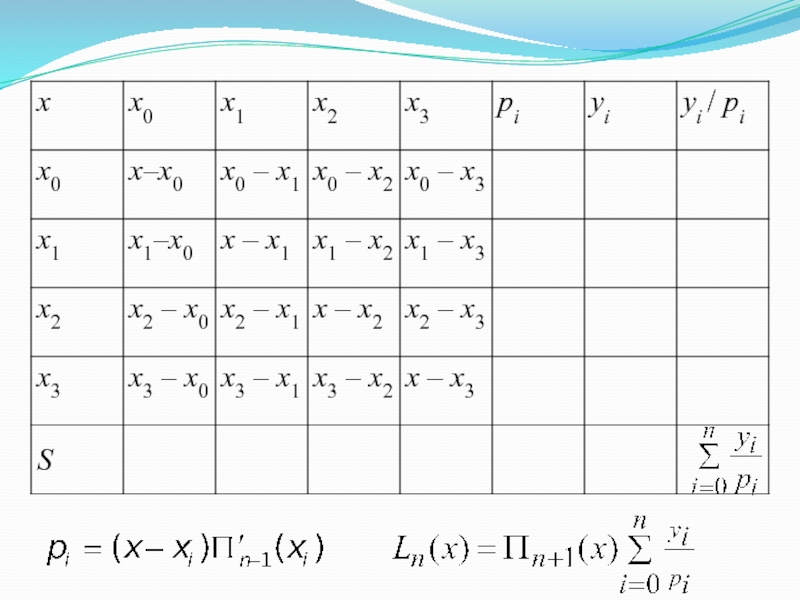
Слайд 324.6. Интерполирование сплайнами
Пусть на [a; b] задана сетка
- множество полиномов степени m
- множество функций, определенных на
[a; b] и имеющих непрерывную т-ю
производную.
- множество функций, определенных на
[a; b] и имеющих непрерывную т-ю
производную.
Слайд 34
Пусть на [a; b] задана сетка
и некоторые числа
Говорят, что сплайн интерполирует функцию f(x) на заданной сетке, если
Слайд 35Узлы сетки - узлы сплайна
Узлы сетки
– узлы интерполяции
Для сплайнов чётной степени
Для сплайнов нечётной степени
Для сплайнов чётной степени
Для сплайнов нечётной степени
Слайд 43Интерполяционным кубическим сплайном, соответствующим данной функции f(x), называется функция s(x), удовлетворяющая
условиям:
Слайд 52
ln F(x) = ln a + mln x
в таблице логарифмируем все значения xi и
yi и находим параметры a = m и b = ln a из системы (*)
Слайд 53
ln F(x) = ln a + mx
В таблице логарифмируем только значения yi
, находим параметры a = m и b = ln a из системы (*)
Слайд 54
В таблице все значения yi заменяются на обратные,
xi остаются без
изменения.
Параметры a и b находятся из системы (*)
Параметры a и b находятся из системы (*)
Слайд 55
Все значения xi заменяются на обратные,
а yi остаются без изменения.
Параметры a и b находятся из системы (*)
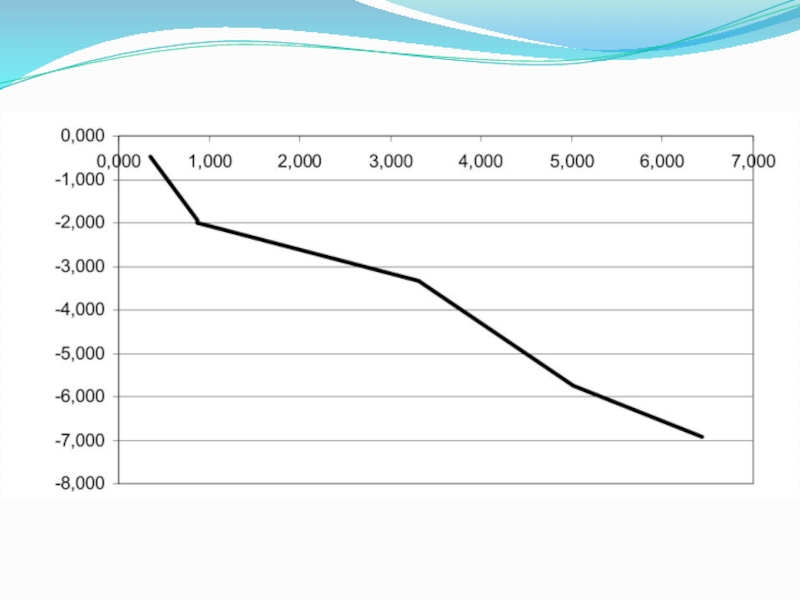
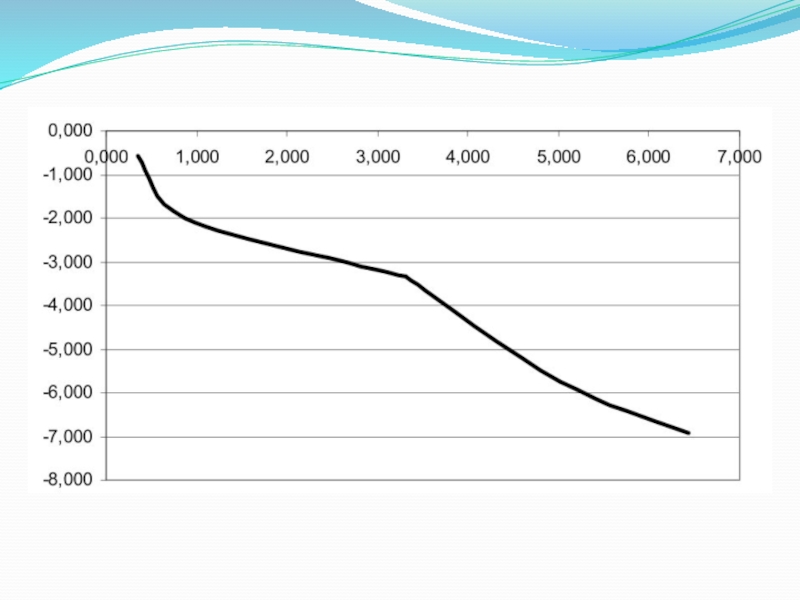
Слайд 58Пример. По заданной таблице значений x и y найти методом наименьших
квадратов эмпирическую формулу
F(x) = ax + b
. (*)















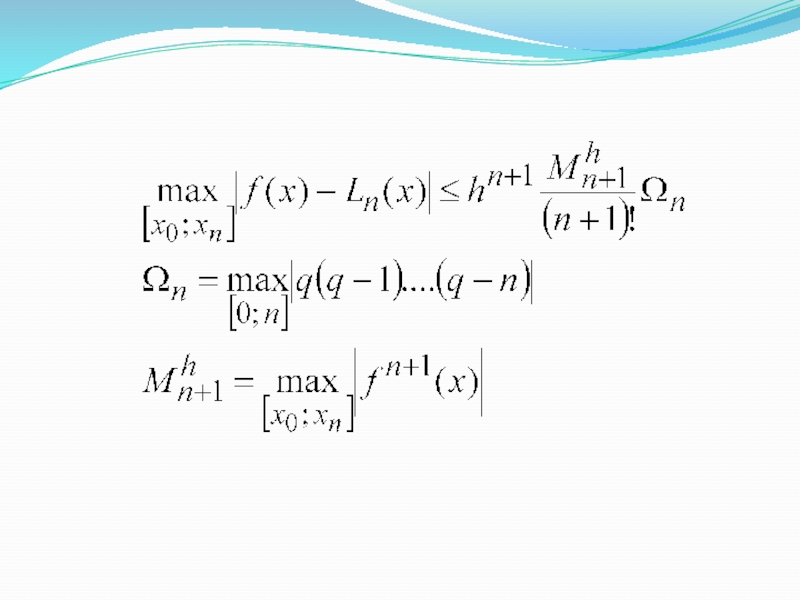













![4.6. Интерполирование сплайнамиПусть на [a; b] задана сетка - множество полиномов степени](/img/tmb/4/363729/5e7636b867636ce65f69eb33468d98e9-800x.jpg)

![Пусть на [a; b] задана сеткаи некоторые числа Говорят,](/img/tmb/4/363729/8577ac4c207f0ec0532e6db9e7b81dca-800x.jpg)