- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Стереометрия. Теория презентация
Содержание
- 1. Стереометрия. Теория
- 2. Параллелепипед- четырехугольная призма, основаниями которой являются параллелограммы. Все шесть граней параллелепипеда- параллелограммы.
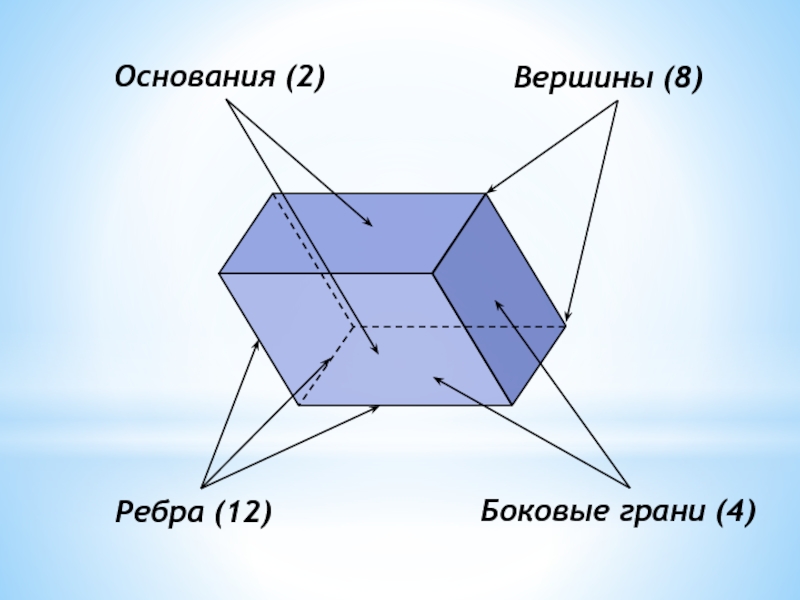
- 3. Ребра (12) Боковые грани (4) Вершины (8) Основания (2)
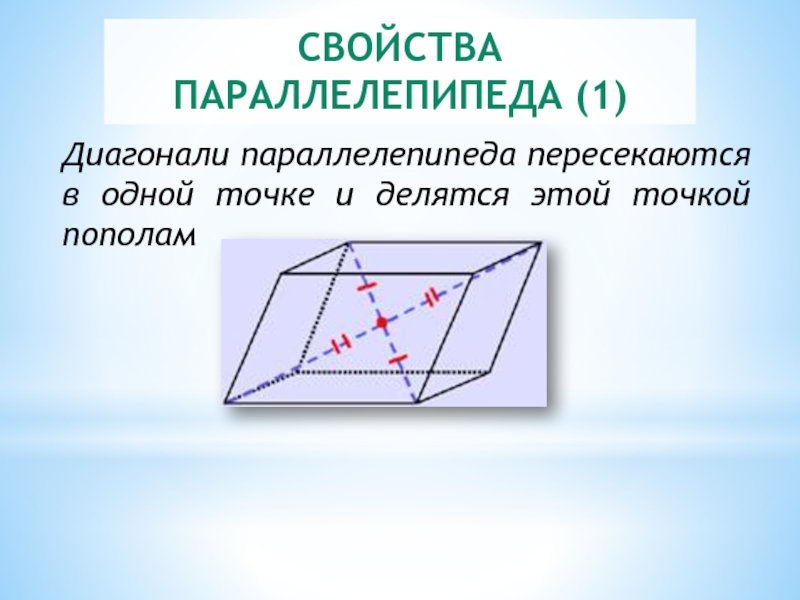
- 5. СВОЙСТВА ПАРАЛЛЕЛЕПИПЕДА (1) Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам
- 6. СВОЙСТВА
- 7. СВОЙСТВА
- 8. СВОЙСТВА
- 9. ПРЯМОЙ ПАРАЛЛЕЛЕПИПЕД Если боковые ребра параллелепипеда перпендикулярны
- 10. ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД Прямой параллелепипед, основания которого являются прямоугольниками называется прямоугольным все грани – прямоугольники
- 11. ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД Длины трех ребер, имеющих общую
- 12. Площадь поверхности а b c Площадь поверхности прямоугольного параллелепипеда равна удвоенной сумме площадей трех граней этого параллелепипеда.
- 13. КУБ Прямоугольный параллелепипед, все грани которого
- 14. Задачи Площадь поверхности куба равна 18. Найдите
- 15. Объемы подобных тел относятся как куб коэффициента
- 16. Задачи Два ребра прямоугольного параллелепипеда, выходящие из
- 17. Определение призмы: Призма — многогранник, две грани которого
- 18. Определение призмы: А1А2…АnВ1В2Вn– призма Многоугольники А1А2…Аn и
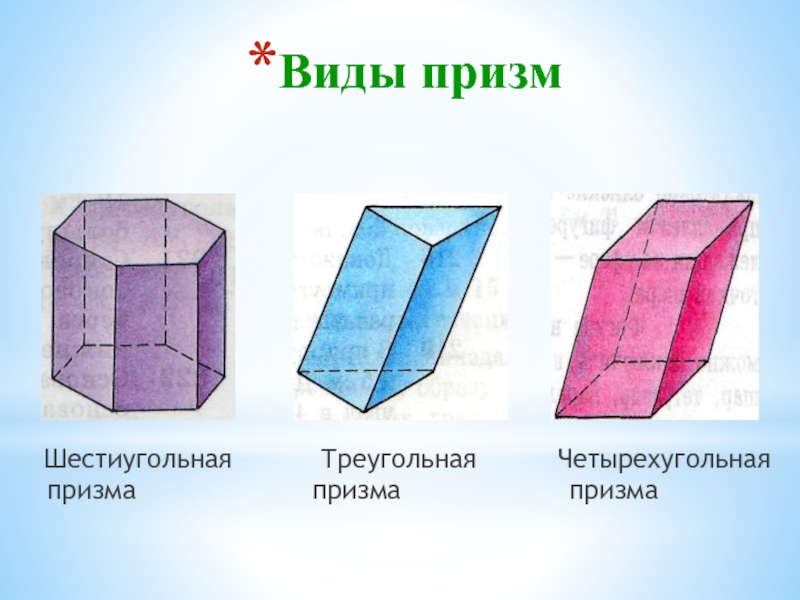
- 19. Виды призм Шестиугольная
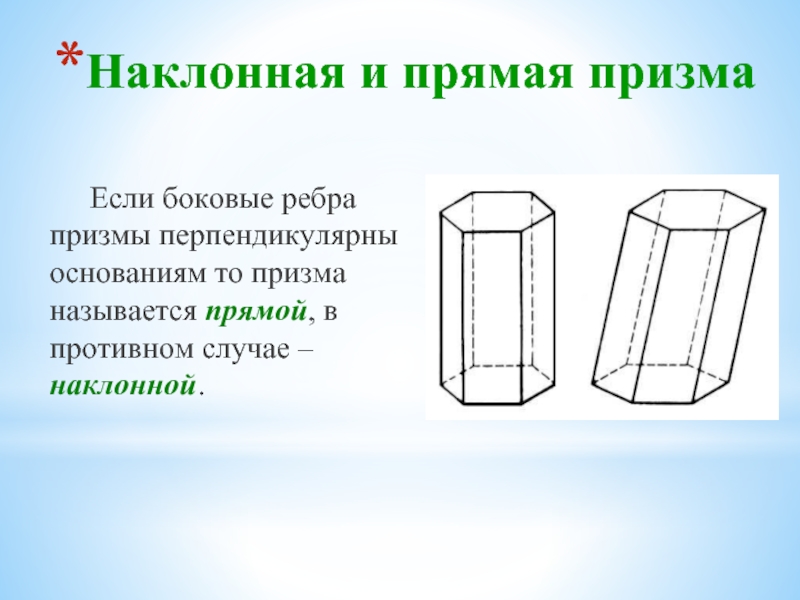
- 20. Наклонная и прямая призма
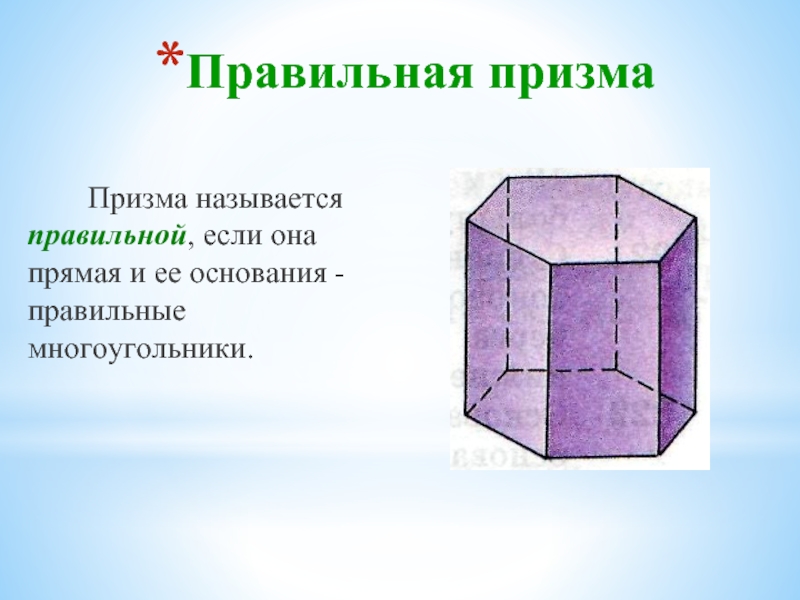
- 21. Правильная призма Призма называется правильной, если она прямая и ее основания - правильные многоугольники.
- 22. Площадь полной поверхности призмы
- 23. Площадь боковой поверхности призмы Теорема
- 24. Объем наклонной призмы Теорема Объем наклонной призмы равен произведению площади основания на высоту.
- 25.
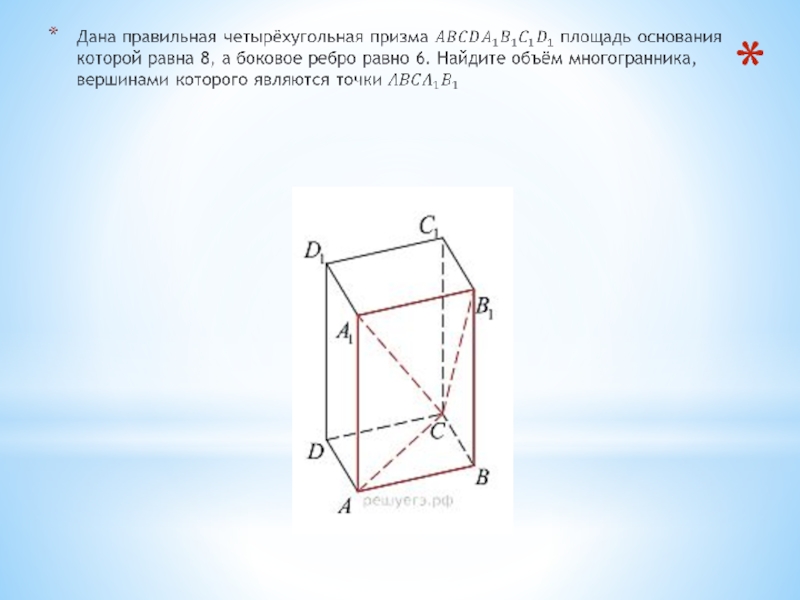
- 26. Найдите объём многогранника, вершинами которого являются вершины
- 28. В цилиндрическом сосуде уровень жидкости достигает 16
Параллелепипед- четырехугольная призма, основаниями которой являются параллелограммы. Все шесть граней параллелепипеда- параллелограммы.
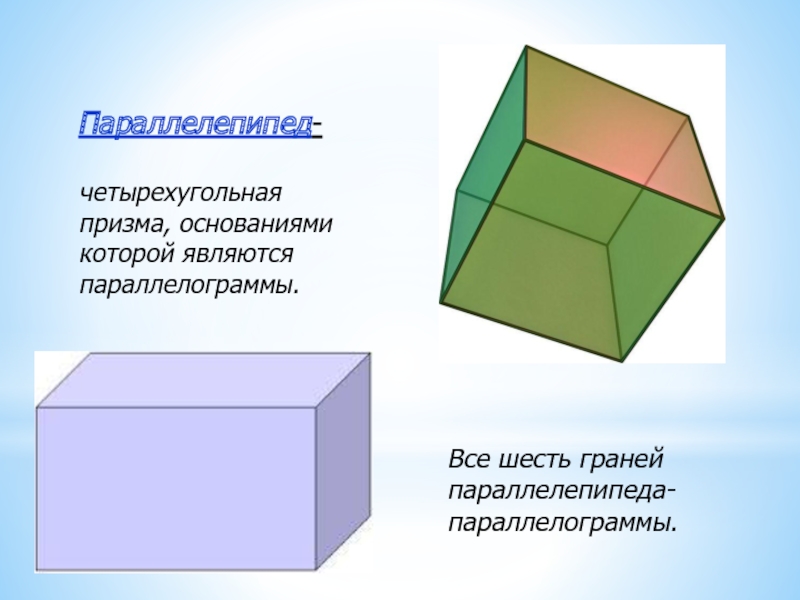
Слайд 2Параллелепипед-
четырехугольная призма, основаниями которой являются параллелограммы.
Все шесть граней параллелепипеда- параллелограммы.
Слайд 5СВОЙСТВА ПАРАЛЛЕЛЕПИПЕДА (1)
Диагонали параллелепипеда пересекаются в одной точке и делятся этой
точкой пополам
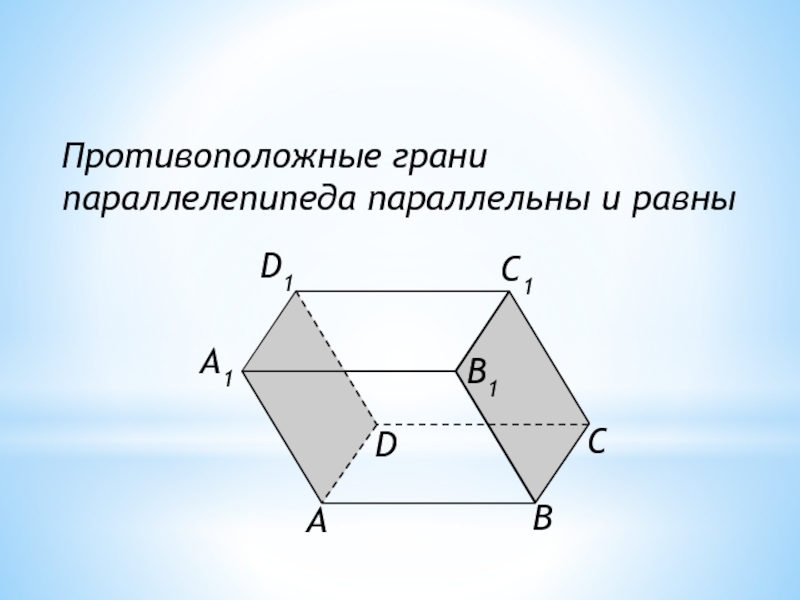
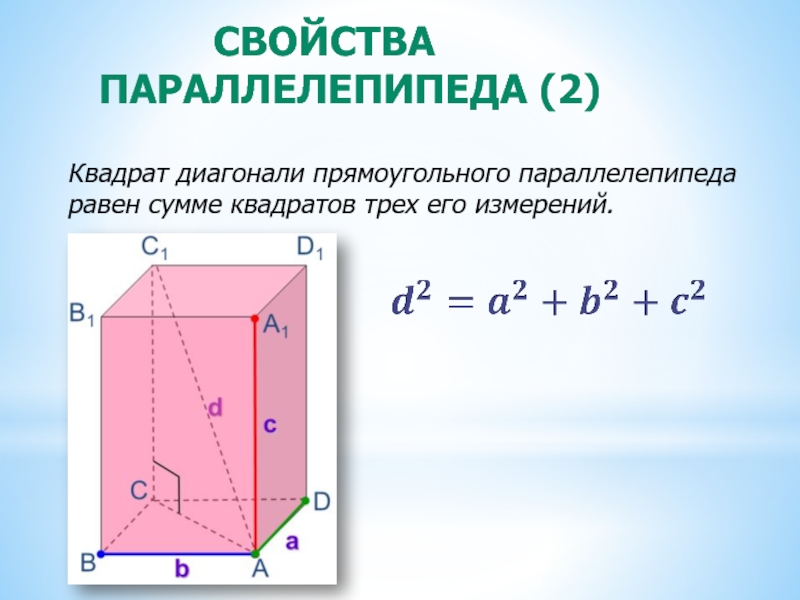
Слайд 6 СВОЙСТВА ПАРАЛЛЕЛЕПИПЕДА (2)
Квадрат диагонали прямоугольного
параллелепипеда равен сумме квадратов трех его измерений.
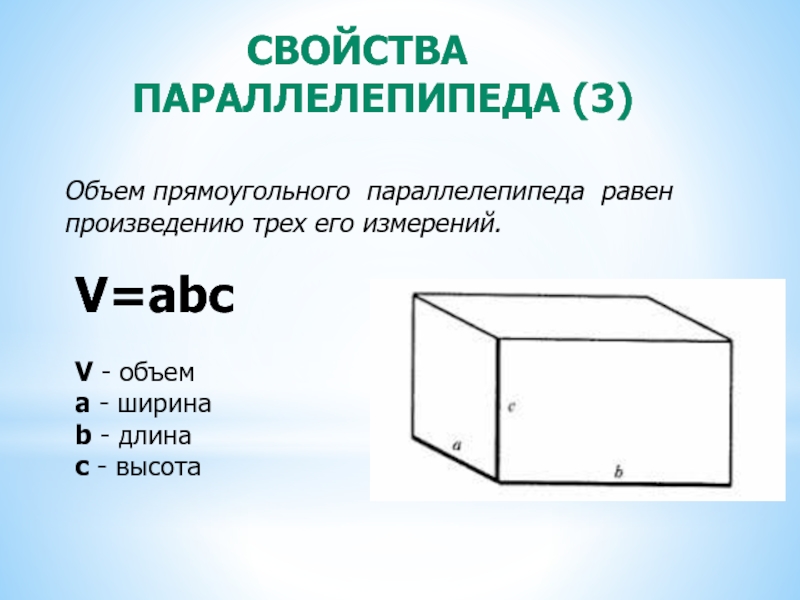
Слайд 7 СВОЙСТВА ПАРАЛЛЕЛЕПИПЕДА (3)
Объем прямоугольного параллелепипеда
равен произведению трех его измерений.
V=abc
V - объем
a - ширина
b - длина
c - высота
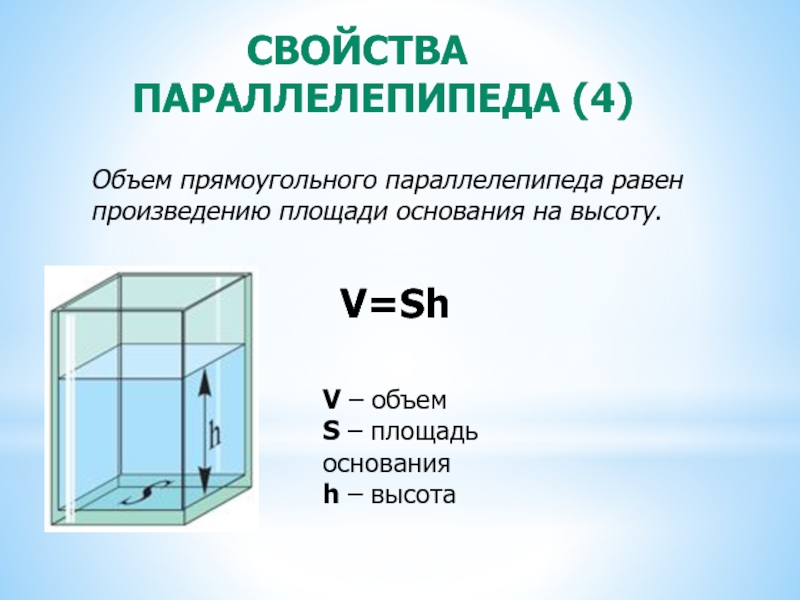
Слайд 8 СВОЙСТВА ПАРАЛЛЕЛЕПИПЕДА (4)
Объем прямоугольного параллелепипеда
равен произведению площади основания на высоту.
V=Sh
V – объем
S – площадь основания
h – высота
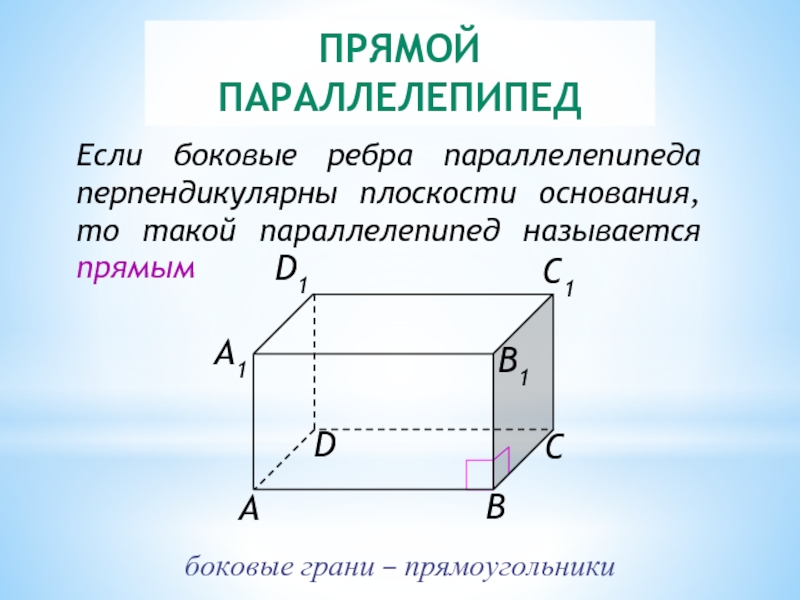
Слайд 9ПРЯМОЙ ПАРАЛЛЕЛЕПИПЕД
Если боковые ребра параллелепипеда перпендикулярны плоскости основания, то такой параллелепипед
называется прямым
боковые грани – прямоугольники
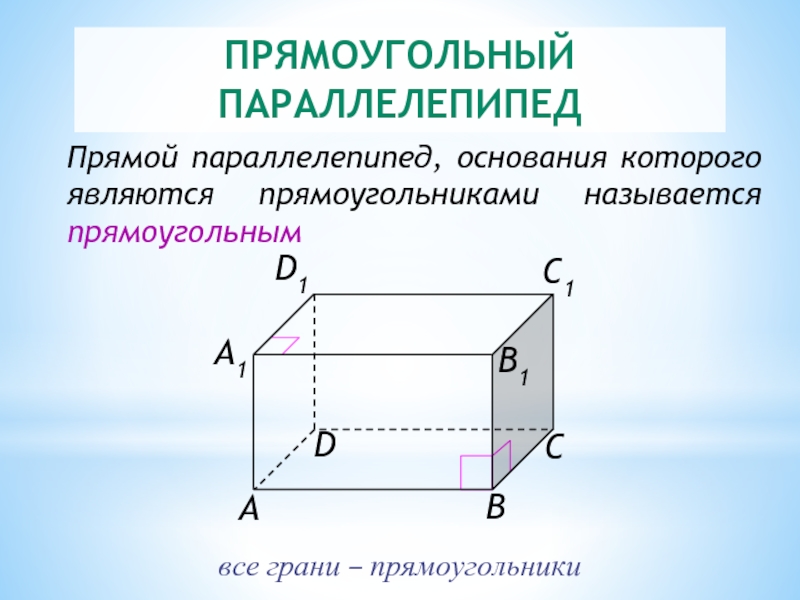
Слайд 10ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД
Прямой параллелепипед, основания которого являются прямоугольниками называется прямоугольным
все грани –
прямоугольники
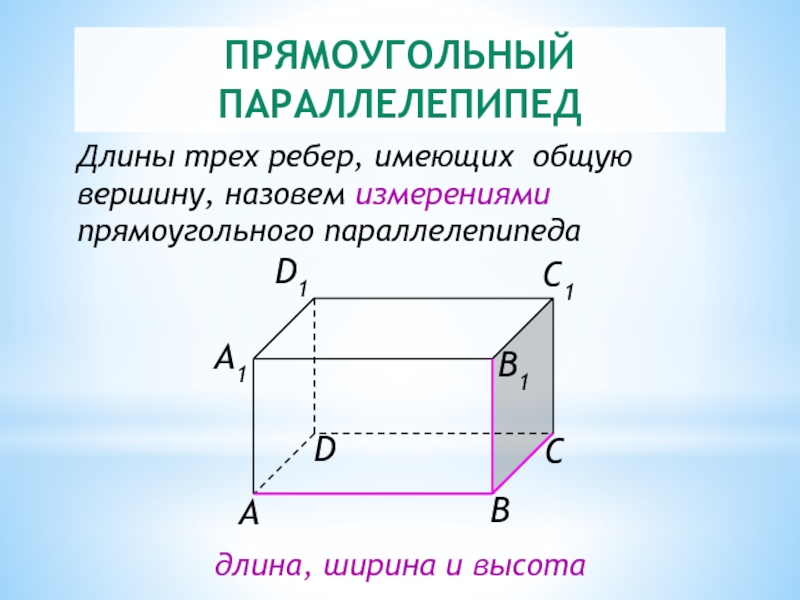
Слайд 11ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД
Длины трех ребер, имеющих общую вершину, назовем измерениями прямоугольного параллелепипеда
длина,
ширина и высота
Слайд 12Площадь поверхности
а
b
c
Площадь поверхности прямоугольного параллелепипеда равна удвоенной сумме площадей трех граней этого параллелепипеда.
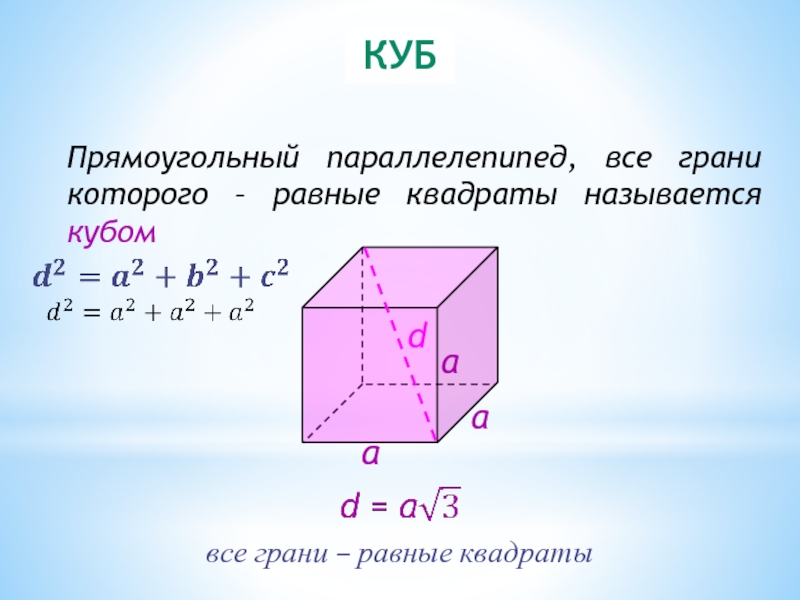
Слайд 13КУБ
Прямоугольный параллелепипед, все грани которого – равные квадраты называется кубом
все
грани – равные квадраты
d
a
a
a
Слайд 14Задачи
Площадь поверхности куба равна 18. Найдите его диагональ.
Объем куба равен 8.
Найдите площадь его поверхности.
Во сколько раз увеличится объем куба, если его ребра увеличить в три раза?
Объем одного куба в 8 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
Во сколько раз увеличится объем куба, если его ребра увеличить в три раза?
Объем одного куба в 8 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
Слайд 15Объемы подобных тел относятся как куб коэффициента подобия.
Площади поверхностей подобных тел
относятся как квадрат коэффициента подобия.
Слайд 16Задачи
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и
4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.
Площадь грани прямоугольного параллелепипеда равна 12. Ребро, перпендикулярное этой грани, равно 4. Найдите объем параллелепипеда.
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.
Площадь грани прямоугольного параллелепипеда равна 12. Ребро, перпендикулярное этой грани, равно 4. Найдите объем параллелепипеда.
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.
Слайд 17Определение призмы:
Призма — многогранник, две грани которого (основания) — равные многоугольники, лежащие в
параллельных плоскостях, а боковые грани — параллелограммы.
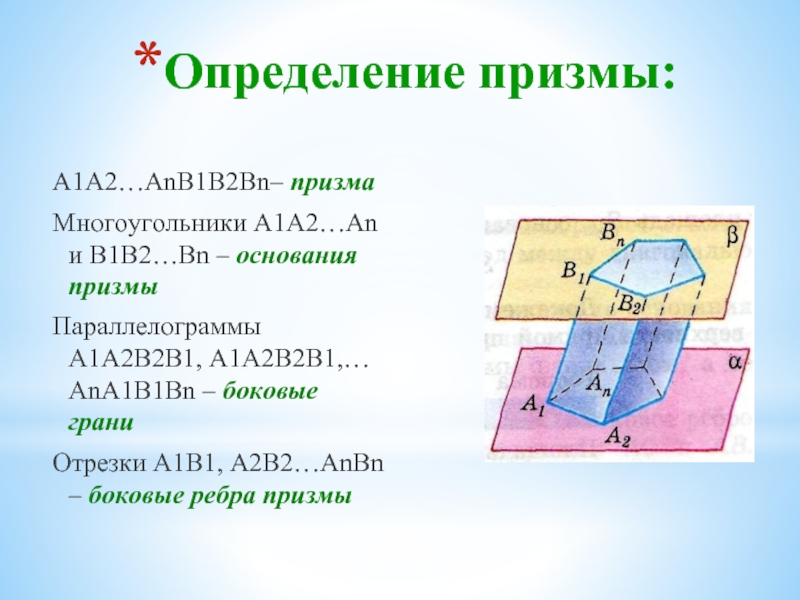
Слайд 18Определение призмы:
А1А2…АnВ1В2Вn– призма
Многоугольники А1А2…Аn и В1В2…Вn – основания призмы
Параллелограммы А1А2В2В1, А1А2В2В1,…
АnА1В1Вn – боковые грани
Отрезки А1В1, А2В2…АnBn – боковые ребра призмы
Отрезки А1В1, А2В2…АnBn – боковые ребра призмы
Слайд 20Наклонная и прямая призма
Если боковые ребра призмы перпендикулярны
основаниям то призма называется прямой, в противном случае – наклонной.
Слайд 21Правильная призма
Призма называется правильной, если она прямая и ее основания -
правильные многоугольники.
Слайд 23Площадь боковой поверхности призмы
Теорема
Площадь боковой поверхности прямой призмы
равна половине произведения периметра основания на высоту призмы.
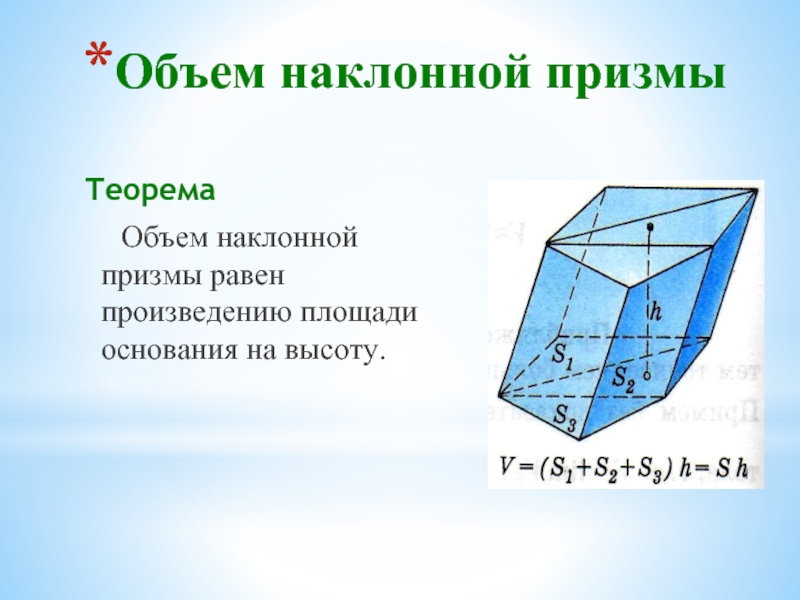
Слайд 24Объем наклонной призмы
Теорема
Объем наклонной призмы равен произведению площади основания на высоту.
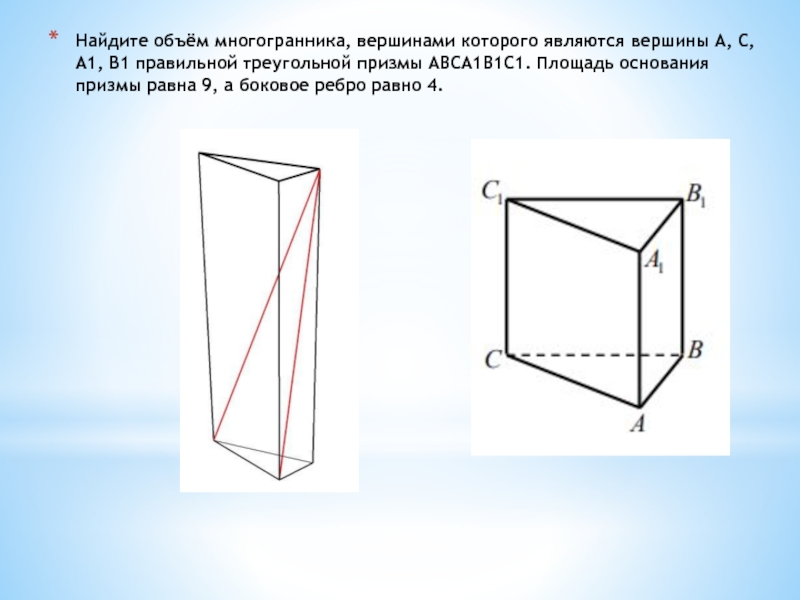
Слайд 26Найдите объём многогранника, вершинами которого являются вершины A, C, A1, B1
правильной треугольной призмы ABCA1B1C1. Площадь основания призмы равна 9, а боковое ребро равно 4.
Слайд 28В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте
будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в раза больше первого? Ответ выразите в см.
