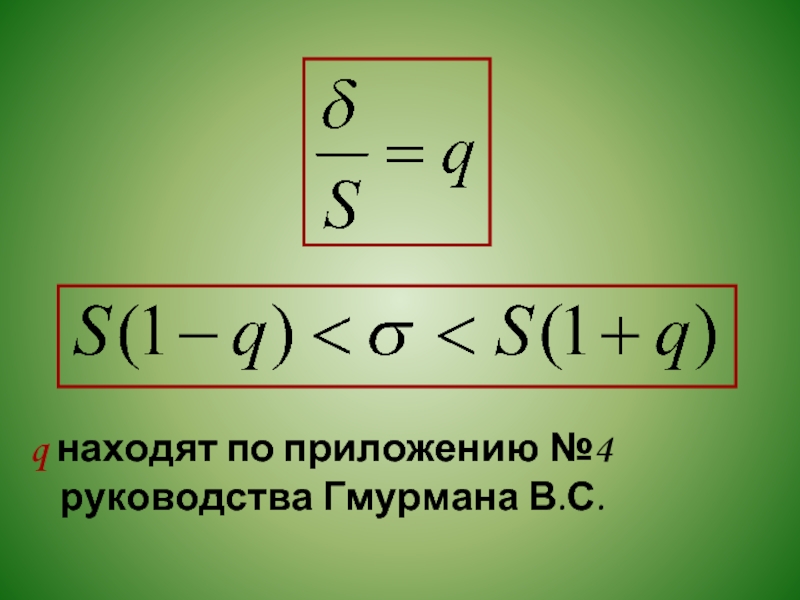- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Статистические оценки параметров распределения. Доверительные интервалы презентация
Содержание
- 1. Статистические оценки параметров распределения. Доверительные интервалы
- 2. Виды статистических ошибок Интервальные оценки Доверительные интервалы
- 3. Виды статистических ошибок Def: Статистической оценкой неизвестного
- 4. Def: Несмещенной называют статистическую оценку Θ*, математическое
- 5. Def: Состоятельной называют статистическую оценку, которая при
- 6. Точечные оценки
- 7. При выборке малого объема точечная оценка может
- 8. Интервальные оценки Интервальные оценки позволяют установить точность
- 9. Т.о., положительное число δ характеризует точность оценки.
- 10. Def: Надежностью (доверительной вероятностью) оценки Θ по
- 11. Заменив неравенство │Θ – Θ*│< δ равносильным
- 12. Доверительный интервал Def: Доверительным интервалом называется случайный
- 13. Доверительный интервал для математического ожидания нормально распределенного
- 14. Приведенная формула позволяет решать следующие задачи: 1)
- 15. В случае большой выборки при n >
- 16. Исследование большой выборки может оказаться невозможным по
- 17. Эта величина соответствует закону t – распределения
- 18. Вероятность попадания случайной величины в соответствующий интервал равна:
- 19. Доверительный интервал для оценки математического ожидания при
- 20. Примечание: при большом объеме выборки (n
- 21. Пример Для определения средней живой массы трехмесячного
- 22. Найти: величины, которые следует принять за
- 23. Решение 1) В качестве приближенного значения средней
- 24. Вычисляем выборочную исправленную дисперсию
- 25. Находим исправленное выборочное среднее квадратичное отклонение
- 26. 2) Ошибка средней равна
- 27. 3) Поскольку n = 100 > 30
- 28. Из условия 2Φ(tγ) = 0.95 определяем
- 29. Замечание: если требуется оценить математическое ожидание с
- 30. Объем выборочной совокупности при повторном способе отбора
- 31. Доверительный интервал для оценки среднего квадратического отклонения σ нормального распределения.
- 32. q находят по приложению №4 руководства Гмурмана В.С.
Слайд 3Виды статистических ошибок
Def:
Статистической оценкой неизвестного параметра теоретического распределения называют функцию от
наблюдаемых случайных величин.
Для того, чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определенным требованиям.
Для того, чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определенным требованиям.
Слайд 4Def:
Несмещенной называют статистическую оценку Θ*, математическое ожидание которой равно оцениваемому параметру
Θ при любом объеме выборки, т.е. M(Θ*) = Θ.
Смещенной, если M(Θ*) ≠ Θ.
Def:
Эффективной называют статистическую оценку, которая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию.
Смещенной, если M(Θ*) ≠ Θ.
Def:
Эффективной называют статистическую оценку, которая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию.
Слайд 5Def:
Состоятельной называют статистическую оценку, которая при n→∞ стремится по вероятности к
оцениваемому параметру.
Оценки бывают точечными, которые определяются одним числом. Все оценки, рассмотренные выше – точечные.
Оценки бывают точечными, которые определяются одним числом. Все оценки, рассмотренные выше – точечные.
Слайд 7При выборке малого объема точечная оценка может разительно отличаться от оцениваемого
параметра, т.е. приводить к грубым ошибкам.
По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.
По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.
Слайд 8Интервальные оценки
Интервальные оценки позволяют установить точность и надежность оценок.
Пусть найденная по
данным выборки статистическая характеристика Θ* служит оценкой неизвестного параметра Θ.
Если δ > 0 и │Θ – Θ*│< δ, то чем меньше δ, тем оценка точнее.
Если δ > 0 и │Θ – Θ*│< δ, то чем меньше δ, тем оценка точнее.
Слайд 9Т.о., положительное число δ характеризует точность оценки.
Однако статистические методы не позволяют
категорически утверждать, что оценка Θ* удовлетворяет неравенству │Θ – Θ*│< δ; можно лишь говорить о вероятности γ, с которой это неравенство осуществляется.
Слайд 10Def:
Надежностью (доверительной вероятностью) оценки Θ по Θ* называют вероятность γ, с
которой осуществляется неравенство
│Θ – Θ*│< δ. γ = 0,95; 0,99; 0,999.
│Θ – Θ*│< δ. γ = 0,95; 0,99; 0,999.
Слайд 11Заменив неравенство │Θ – Θ*│< δ равносильным уме двойным неравенством
Вероятность
того, что интервал
(Θ* - δ; Θ* + δ) заключает в себе (покрывает) неизвестный параметр Θ, равна γ.
Слайд 12Доверительный интервал
Def:
Доверительным интервалом называется случайный интервал (Q* - δ; O* +
δ), в пределах которого с вероятностью γ находится неизвестный оцениваемый параметр.
Доверительные интервалы находят по различным формулам, в зависимости от исходных данных.
Доверительные интервалы находят по различным формулам, в зависимости от исходных данных.
Слайд 13Доверительный интервал для математического ожидания нормально распределенного признака с известным средним
квадратическим отклонением находят по формуле:
где - среднее квадратическое отклонение, t – параметр, величину которого находят по таблицам Лапласа из соотношения γ=2Φ(t).
где - среднее квадратическое отклонение, t – параметр, величину которого находят по таблицам Лапласа из соотношения γ=2Φ(t).
Слайд 14Приведенная формула позволяет решать следующие задачи:
1) По заданным надежности γ и
объеме выборки n находить точность δ и доверительный интервал.
2) По заданным надежности γ и точности δ находить объем выборки n.
3) По заданным точности δ и объеме выборки n находить надежность γ.
2) По заданным надежности γ и точности δ находить объем выборки n.
3) По заданным точности δ и объеме выборки n находить надежность γ.
Слайд 15В случае большой выборки при n > 30 и неизвестном среднем
квадратическом отклонении σ(X) доверительный интервал находят по формуле:
где S – исправленное выборочное среднее квадратическое отклонение, то есть оценка σ(X).
где S – исправленное выборочное среднее квадратическое отклонение, то есть оценка σ(X).
Слайд 16Исследование большой выборки может оказаться невозможным по различным признакам. Кроме этого,
с уменьшением n доверительный интервал увеличивается.
При определении доверительного интервала в случае нормального распределения при неизвестном σ признака X в генеральной совокупности применяют случайную величину:
При определении доверительного интервала в случае нормального распределения при неизвестном σ признака X в генеральной совокупности применяют случайную величину:
Слайд 17Эта величина соответствует закону t – распределения Стьюдента.
Дифференциальная функция распределения T
обозначается S(tγ; n) и зависит только от объема выборки n.
Слайд 19Доверительный интервал для оценки математического ожидания при неизвестном σ.
где tγ =
t(γ; n) – числа, приведенные в специальных таблицах.
Слайд 20Примечание: при большом объеме выборки (n ≥ 30) значения tγ таблицы
Стьюдента и
t таблицы Лапласа практически равны. Поэтому выбор формулы, по которой определяют доверительный интервал, диктуется исходными данными.
Слайд 21Пример
Для определения средней живой массы трехмесячного теленка определенной породы были взвешены
100 животных и результаты сведены в таблицу
Слайд 22Найти:
величины, которые следует принять за среднюю массу и среднее квадратическое
отклонение;
ошибку средней и коэффициетнт вариаций;
доверительный интервал, в котором с вероятностью 0,95 заключена средняя масса.
ошибку средней и коэффициетнт вариаций;
доверительный интервал, в котором с вероятностью 0,95 заключена средняя масса.
Слайд 23Решение
1) В качестве приближенного значения средней массы принимаем выборочную среднюю, а
за значение признака – середины интервалов
Слайд 273) Поскольку n = 100 > 30 и у нас случай
нормального распределения, то доверительный интервал находим по формуле
Слайд 28Из условия 2Φ(tγ) = 0.95 определяем Φ(tγ) = 0,475, а по
таблице приложений находим tγ = 1,96.
Поэтому
или 31,32 < x < 32,68 кг – доверительный интервал для заданной вероятности.
Поэтому
или 31,32 < x < 32,68 кг – доверительный интервал для заданной вероятности.
Слайд 29Замечание: если требуется оценить математическое ожидание с наперед заданной точностью δ
и надежностью γ, то максимальный объем выборки, который обеспечит эту точность, находится по формуле
Слайд 30Объем выборочной совокупности при повторном способе отбора находят по формуле:
где параметр
t определяют из
по таблицам Лапласа;
Слайд 31Доверительный интервал для оценки среднего квадратического отклонения σ нормального распределения.
