вариационного ряда, его виды и графическое изображение
Показатели вариации. Порядок их построения
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Средние величины и показатели вариации презентация
Содержание
- 1. Средние величины и показатели вариации
- 2. ФОРМЫ И ВИДЫ СРЕДНИХ ВЕЛИЧИН
- 3. Рекомендации при использовании средних величин
- 4. Простые и взвешенные средние Для
- 5. Простые и взвешенные средние
- 6. Взвешенная средняя равна простой в трех
- 7. Задача
- 8. Решение
- 9. Правило мажорантности средних
- 10. СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ВАРИАЦИИ
- 11. Ряд распределения – упорядоченное распределение единиц
- 12. Виды вариационных рядов
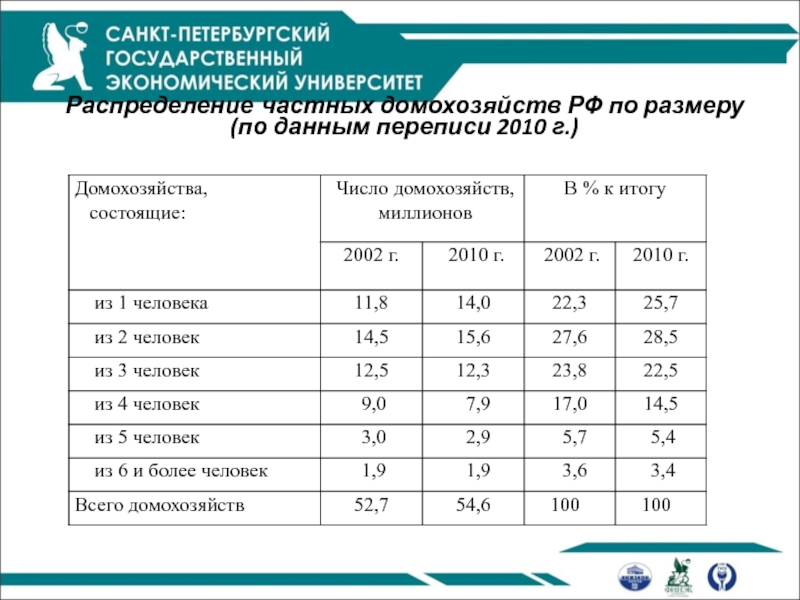
- 13. Распределение частных домохозяйств РФ
- 15. Элементы вариационного ряда Варианты
- 17. Расчет числа интервалов
- 18. Расчет величины интервалов
- 19. Плотность распределения Если в
- 20. Отношение частоты интервала к ширине этого
- 21. Графическое изображение вариационного
- 22. Полигон распределения
- 23. Полигон распределения
- 24. Гистограмма, кумулята
- 25. Показатели вариации Размах вариации
- 26. Показатели вариации Дисперсия:
- 27. Показатели вариации Среднее квадратическое отклонение
- 28. Показатели вариации Коэффициент вариации
- 29. Шкала значений коэффициента вариации
- 30. Показатели вариации Мода – наиболее часто встречающееся в данной совокупности значение признака
- 31. В дискретном ряду мода – вариант
- 32. Показатели вариации
- 33. В дискретном ряду медиана определяется по
- 34. Показатели вариации В интервальном ряду медиана определяется по формуле:
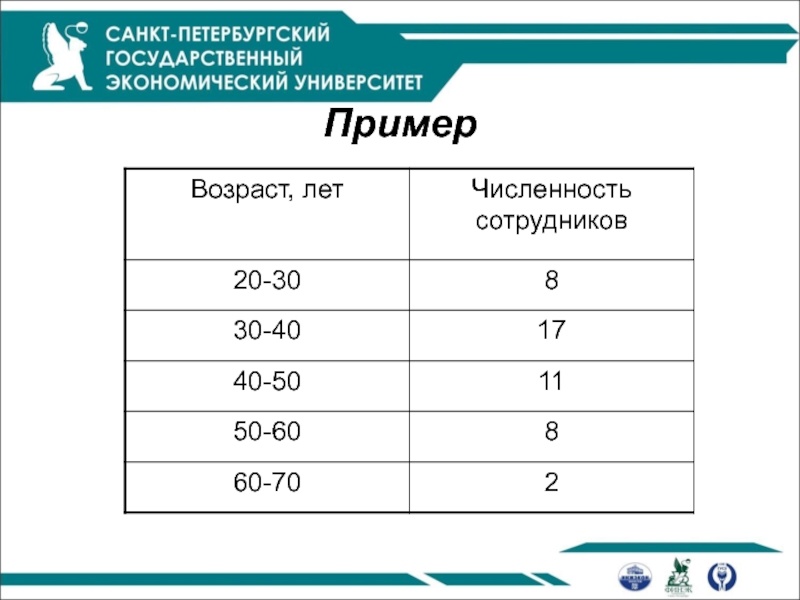
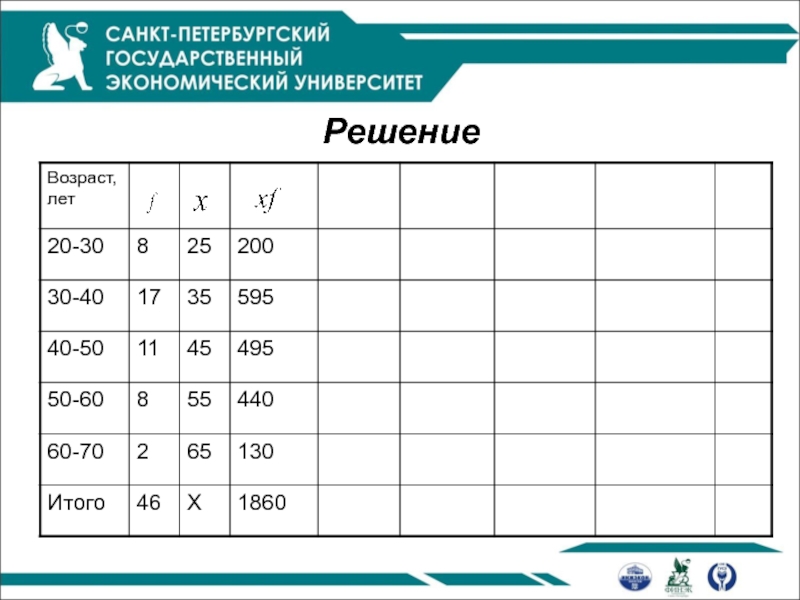
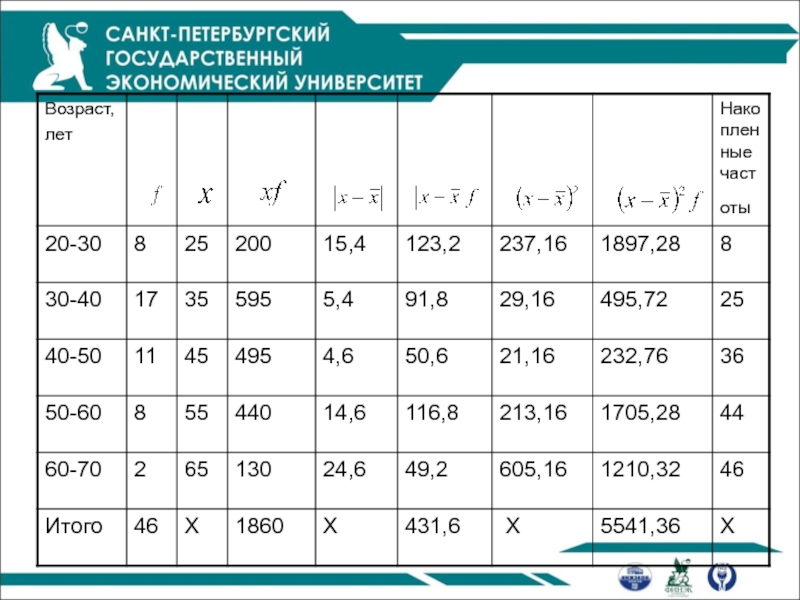
- 35. Пример Имеются данные о
- 36. Решение
- 37. Пример
- 38. Решение
- 39. Решение
- 43. Квартили – делят совокупность на 4
- 44. Децили – делят совокупность на 10
- 45. Показатели асимметрии
- 46. Показатели асимметрии
- 47. Средняя квадратическая ошибка коэффициента асимметрии
- 48. Структурный коэффициент асимметрии (формула Пирсона)
- 49. ЭКСЦЕСС
- 50. ЭКСЦЕСС
- 51. Средняя квадратическая ошибка коэффициента эксцесса
- 52. ЭКСЦЕСС Положительный эксцесс
- 53. ЭКСЦЕСС В плосковершинном распределении
Слайд 3
Рекомендации при использовании средних величин
Совокупность, по которой производится обобщение, должна быть
однородной
Необходимо обеспечить исчерпывающий учет единиц совокупности
При расчете средних необходимо учитывать своеобразие и взаимосвязь признаков и использовать их в совокупности с другими статистическими показателями
Порядок расчета средних сохраняется независимо от уровня обобщения
Необходимо обеспечить исчерпывающий учет единиц совокупности
При расчете средних необходимо учитывать своеобразие и взаимосвязь признаков и использовать их в совокупности с другими статистическими показателями
Порядок расчета средних сохраняется независимо от уровня обобщения
Слайд 4
Простые и взвешенные средние
Для расчета средних первичных признаков используется простая средняя
Для
расчета средних вторичных признаков используется взвешенная средняя
Взвешенная средняя может быть рассчитана для первичных признаков, если они представлены в сгруппированном виде
Несгруппированные данные осредняются по простой средней
Взвешенная средняя может быть рассчитана для первичных признаков, если они представлены в сгруппированном виде
Несгруппированные данные осредняются по простой средней
Слайд 5
Простые и взвешенные средние
Простые и взвешенные средние различаются:
по величине (не всегда)
по
способу вычисления
по своей роли в решении различных статистических задач
по своей роли в решении различных статистических задач
Слайд 6
Взвешенная средняя равна простой в трех случаях:
если изучаемый признак не варьирует
если
не варьирует признак-вес
если между осредняемым признаком и признаком-весом нет линейной зависимости
если между осредняемым признаком и признаком-весом нет линейной зависимости
Слайд 10
СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ВАРИАЦИИ
Вариация – это различие значений признака у отдельных единиц
изучаемой совокупности в один и тот же период или момент времени
Вариация отражает колеблемость индивидуальных значений признака
Вариация отражает неравномерность развития единиц совокупности
Вариация отражает колеблемость индивидуальных значений признака
Вариация отражает неравномерность развития единиц совокупности
Слайд 11
Ряд распределения – упорядоченное распределение единиц совокупности по возрастающим или убывающим
значениям признака
Ряд распределения, построенный по качественному признаку – атрибутивный ряд
Ряд распределения, построенный по количественному признаку – вариационный ряд
Ряд распределения, построенный по качественному признаку – атрибутивный ряд
Ряд распределения, построенный по количественному признаку – вариационный ряд
Слайд 12
Виды вариационных рядов
Дискретные, в которых значения варьирующего признака выражены в
виде вполне определенных величин (обычно целых).
Интервальные, в которых значения варьирующего признака представлены в виде интервалов.
Интервальные, в которых значения варьирующего признака представлены в виде интервалов.
Слайд 15
Элементы вариационного ряда
Варианты – значения, которые принимает исследуемый признак
Частоты – абсолютная
численность отдельных групп с различными значениями признака
Частости – удельные веса (доли) отдельных групп в общей численности совокупности
Частости – удельные веса (доли) отдельных групп в общей численности совокупности
Слайд 16
Порядок построения интервальных вариационных рядов
Определяется число групп (число интервалов)
При определении числа
групп учитывается объем совокупности с тем, чтобы обеспечить заполненность интервалов
Определяется величина интервала
Определяется величина интервала
Слайд 17
Расчет числа интервалов
Формула Стерджесса:
или
где: k -число интервалов; n - объем
совокупности.
Слайд 18
Расчет величины интервалов
Где:
- максимальное и минимальное значения признака в вариационном ряду.
Слайд 19
Плотность распределения
Если в интервальном вариационном ряду ширина интервала отлична от единицы,
то определяют абсолютную и относительную плотности распределения
Слайд 20
Отношение частоты интервала к ширине этого интервала называют абсолютной плотностью распределения
для i-го интервала
Относительной плотностью распределения для i-го интервала называют отношение относительной частоты интервала к его ширине
Относительной плотностью распределения для i-го интервала называют отношение относительной частоты интервала к его ширине
Слайд 21
Графическое изображение вариационного ряда
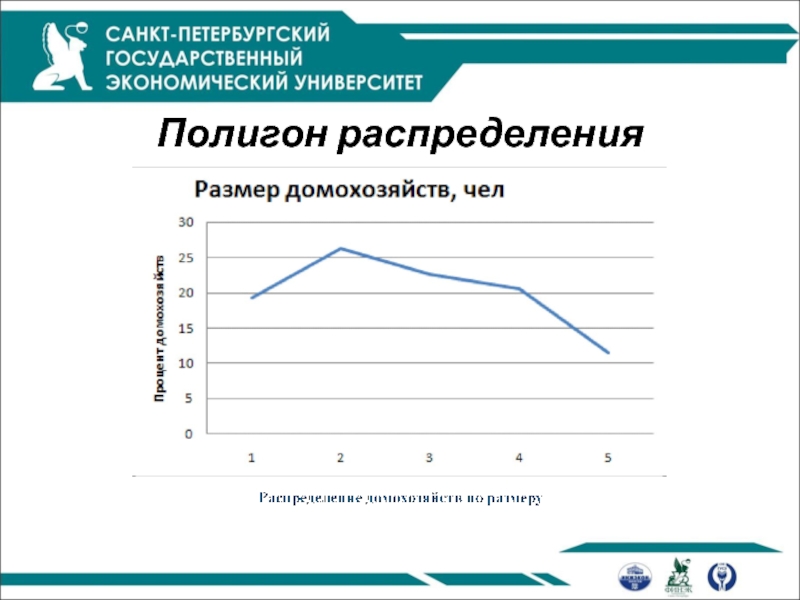
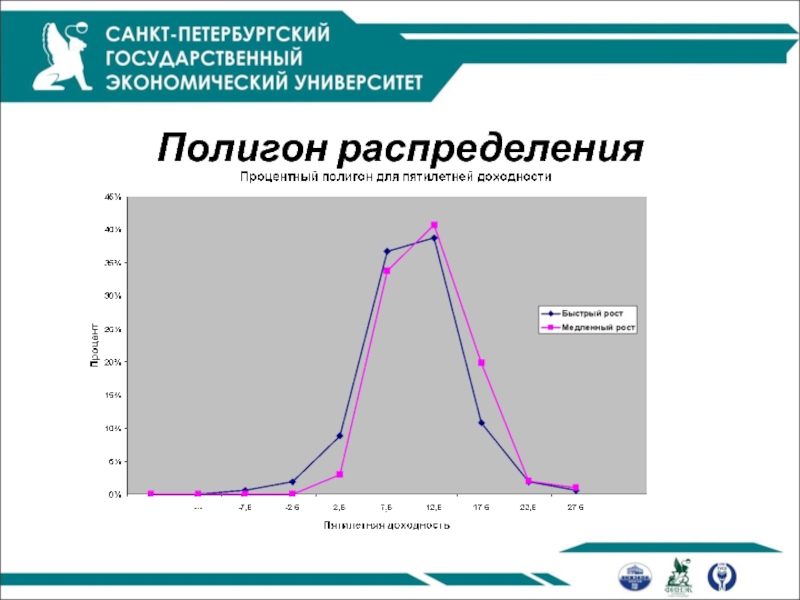
Полигон распределения
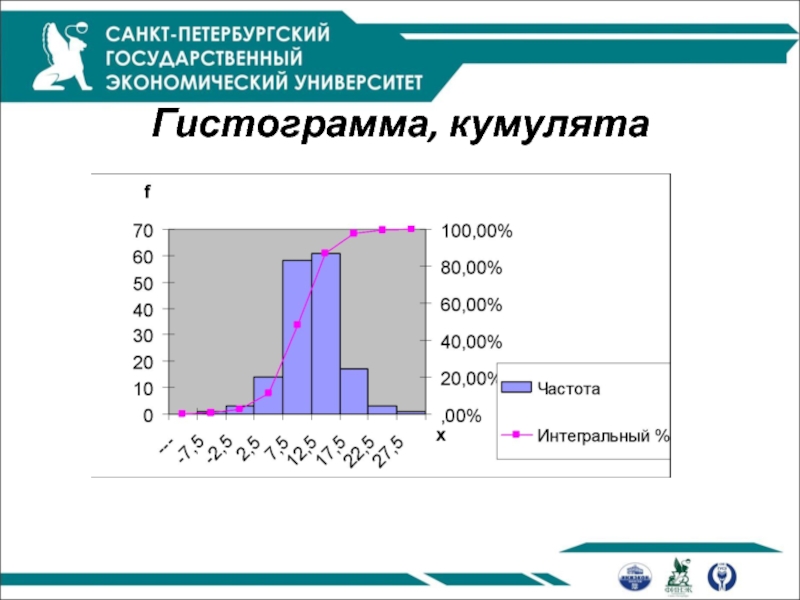
Гистограмма – столбиковая диаграмма, для построения которой
на оси абсцисс откладывают отрезки, равные величине интервалов вариационного ряда
Кумулята распределения строится по накопленным частотам (частостям). Накопленные частоты (частости) определяются последовательным суммированием частот (частостей)
Кумулята распределения строится по накопленным частотам (частостям). Накопленные частоты (частости) определяются последовательным суммированием частот (частостей)
Слайд 25
Показатели вариации
Размах вариации
Среднее линейное отклонение
а) для несгруппированных данных
б) для
сгруппированных данных
Слайд 27
Показатели вариации
Среднее квадратическое отклонение
а) для несгруппированных данных
б) для сгруппированных данных
Слайд 28
Показатели вариации
Коэффициент вариации
Среднее значение признака
для несгруппированных данных
для сгруппированных данных
Слайд 30
Показатели вариации
Мода – наиболее часто встречающееся в данной совокупности значение признака
Слайд 31
В дискретном ряду мода – вариант с наибольшей частотой
В интервальном
ряду мода определяется по формуле:
Слайд 32
Показатели вариации
Медиана – то значение признака, которое находится в середине упорядоченного
ряда и делит совокупность на две равные части
Слайд 33
В дискретном ряду медиана определяется по сумме накопленных частот, которая должна
превышать половину всей численности совокупности
Слайд 35
Пример
Имеются данные о численности работников по 6 магазинам: 7
4 9 7 3 12
Необходимо рассчитать показатели вариации и описать форму распределения этих данных.
Необходимо рассчитать показатели вариации и описать форму распределения этих данных.
Слайд 52
ЭКСЦЕСС
Положительный эксцесс свидетельствует о том, что в совокупности есть слабо варьирующее
по данному признаку «ядро»
Чем круче распределение, тем ярче проявляется закономерность в формировании значений показателей
Чем круче распределение, тем ярче проявляется закономерность в формировании значений показателей
Слайд 53
ЭКСЦЕСС
В плосковершинном распределении единицы рассеяны по всем значениям признака более равномерно.
При существенном отрицательном эксцессе результаты анализа не надежны.
Значительный отрицательный эксцесс может указывать на качественную неоднородность совокупности.