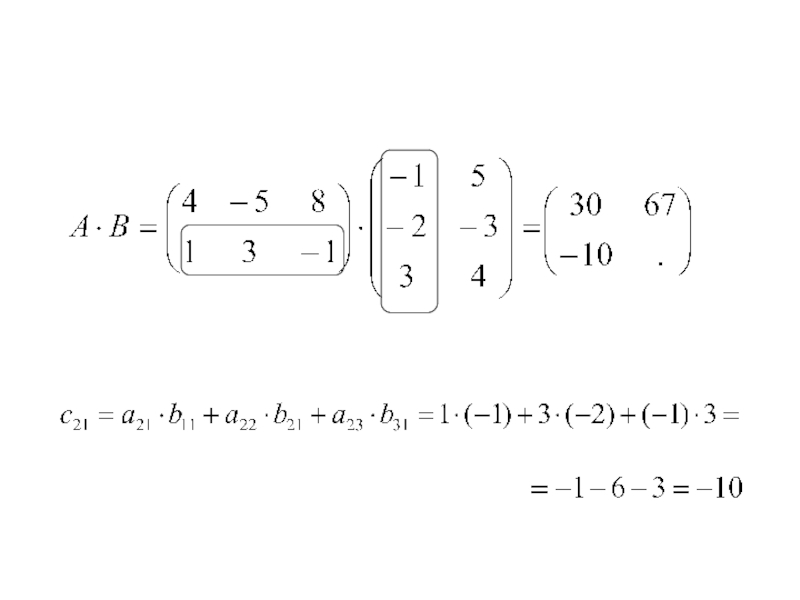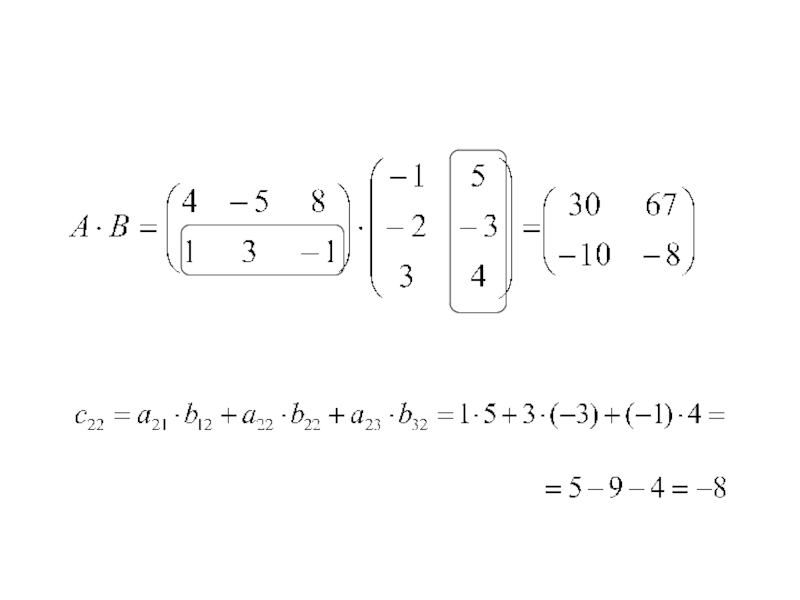- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Матрицы и операции над ними презентация
Содержание
- 1. Матрицы и операции над ними
- 4. Если у матрицы m строк и
- 11. Линейные операции над матрицами. Суммой матриц A=(aij)
- 12. Найти А + В и А -
- 13. Свойства сложения матриц: А+В=В+А закон коммутативности
- 14. Произведением матрицы A=(aij) на число к∈R, называется
- 15. Свойства умножения матрицы на число: 1) (а+b)А=аА+bА
- 16. Произведением матриц Am×n=(aij) и Bn×p=(bjk) называется матрица
- 17. Найти А·В и B·A:
- 21. Найти А·В и B·A:
- 22. умножение матриц имеет смысл только в том
- 23. Свойства умножения матриц: АВ≠ВА
- 24. Если АВ=ВА, то матрица А и В называются перестановочными или коммутирующими.
- 25. Если в диагональной матрице
- 26. Если в матрице переставить строки местами со
- 27. Матрица называется симметричной, если
- 28. Свойства транспонированной матрицы:
- 29. Даны матрицы А и В: Вычислить:
- 30. Каков порядок матриц А и
- 31. Каков порядок матриц А и
Матрицей называется множество чисел, образующих прямоугольную таблицу, которая содержит m строк и n столбцов.
Слайд 2
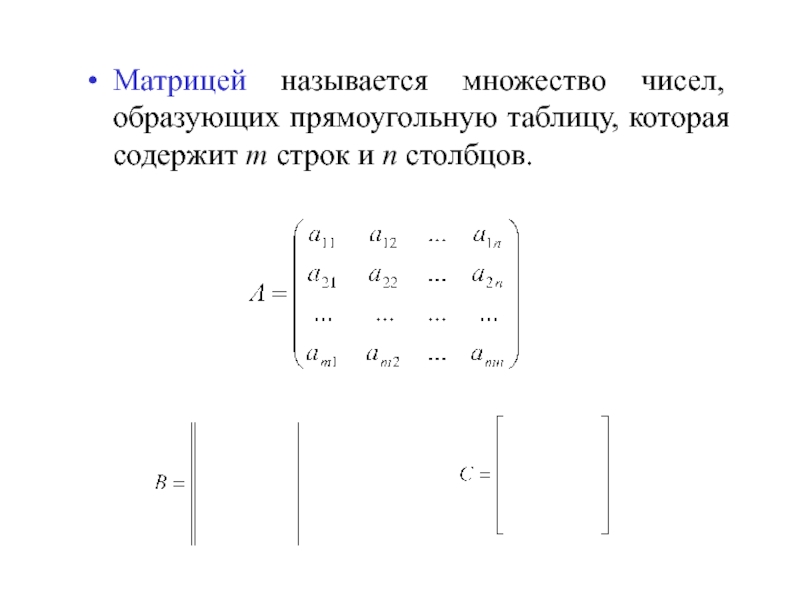
Матрицей называется множество чисел, образующих прямоугольную таблицу, которая содержит m
строк и n столбцов.
Слайд 4
Если у матрицы m строк и n столбцов, то она имеет
размерность m×n (прямоугольная матрица)
Am×n или
Am×n или
Если m=n, то матрица называется квадратной.
Число строк или стобцов квадратной матрицы называется её порядком.
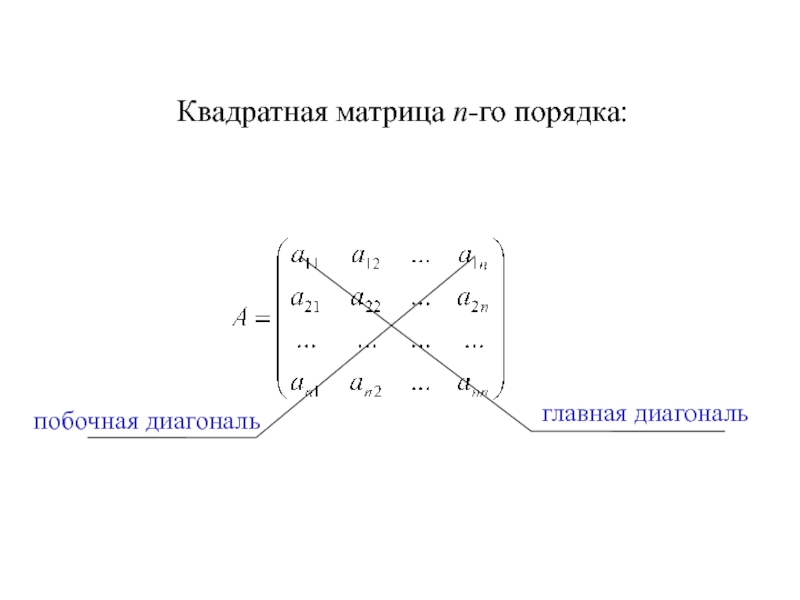
Слайд 6
Если у квадратной матрицы отличны от нуля только элементы, лежащие
на главной диагонали, то такие матрицы называются диагональными.
Слайд 7
Матрица, у которой все элементы, лежащие выше (ниже) главной диагонали
– нули, называется треугольной.
Слайд 9
Дана прямоугольная матрица m×n .
Если m=1, то получаем матрицу-строку:
Если
n=1, то получаем матрицу-столбец:
Слайд 10
Две матрицы называются равными, если они одинаковой размерности и соответствующие
элементы равны.
Т.е, пусть A=(aij) и B=(bij):
Т.е, пусть A=(aij) и B=(bij):
Слайд 11Линейные операции над матрицами.
Суммой матриц A=(aij) и B=(bij) называется матрица C=(cij)
(А+В=С), элементы которой равны сумме соответствующих элементов матриц А и В: cij=aij+bij, причем
Слайд 13Свойства сложения матриц:
А+В=В+А закон коммутативности
2) (А+В)+С=А+(В+С) закон ассоциативности
3) , что А+0=0+А=А
4) ∀А
∃В: А+В=В+А=0, т.е. В=-А
(матрица, противоположная матрице А).
(матрица, противоположная матрице А).
Слайд 14Произведением матрицы A=(aij) на число к∈R, называется матрица кА, каждый элемент
которой равен кaij: кА=(каij)
Слайд 15Свойства умножения матрицы на число:
1) (а+b)А=аА+bА
закон дистрибутивности относительно сложения чисел
2) a(А+В)=aА+aB
закон дистрибутивности относительно сложения матриц
3) (ab)A=a(bA)
4) 1·A=A ∀А
Слайд 16Произведением матриц Am×n=(aij) и Bn×p=(bjk) называется матрица Cm×p=(cik)=A·B, элементы которой
где i=1,2,…,m k=1,2,…,p
Слайд 22умножение матриц имеет смысл только в том случае, когда число столбцов
первой матрицы равно числу строк второй.
в результате умножения получается матрица с количеством строк первой и количеством столбцов второй.
в результате умножения получается матрица с количеством строк первой и количеством столбцов второй.
Слайд 23Свойства умножения матриц:
АВ≠ВА
А(ВС)=(АВ)С закон ассоциативности
(А+В)С=АС+ВС закон дистрибутивности
Если ∃АВ, то а(АВ)=(аА)В=А(аВ), а∈R
5) Произведение двух ненулевых матриц может быть нулевой матрицей.
Слайд 25
Если в диагональной матрице все элементы главной диагонали 1, то матрица
называется единичной.
Свойство: ЕА=АЕ=А
Свойство: ЕА=АЕ=А
Слайд 26Если в матрице переставить строки местами со столбцами, то получим матрицу,
которая называется транспонированной:
